代码随想录算法训练营Day18 | 二叉搜索树中的插入操作、二叉搜索树的最近公共祖先、删除二叉搜索树的节点、修剪二叉搜索树、二叉搜索树转换成累加树、将有序数组转换成二叉搜索树

LeetCode 701 二叉搜索树的插入操作

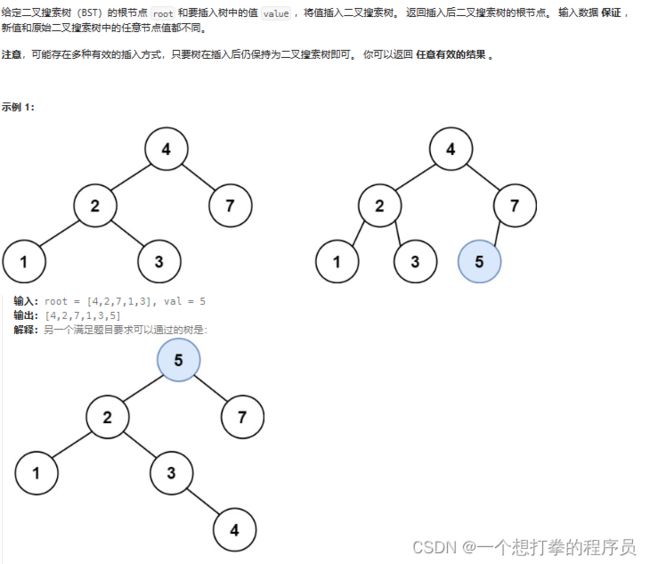
本题思路：既然是二叉搜索树，那么插入就变得比较简单了。因为二叉搜索树的左树节点值都小于根节点值，右树节点值都大于根节点值。

直接将要插入的节点值和根节点进行对比，如果比它小，就往左孩子走，比他大，就往右孩子走。最右直到为空的时候，此时这个位置就是要插入的位置。 再移动的过程中，可以用一个指针来记录父节点的位置。再定义一个标识来判断是走的左孩子还是右孩子。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        TreeNode node = new TreeNode(val);
        TreeNode cur = root;
        TreeNode pre = null;
        boolean flag = true;
        if(cur == null){
            return node;
        }
        while(cur != null){
            if(node.val > cur.val){
                pre = cur;
                cur = cur.right;
                flag = true;
            }else{
                pre = cur;
                cur = cur.left;
                flag = false;
        }
        }
        if(flag){
            pre.right = node;
        }else{
            pre.left = node;
        }
        return root;
    }
}

---

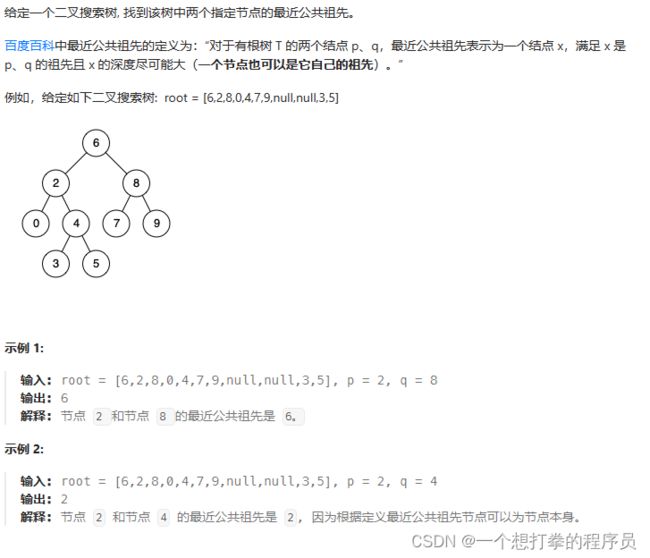
LeetCode 235 二叉搜索树的最近公共祖先

本题思路：使用后序遍历。首先判断一些边界条件，递归的出口。

• 如果根节点为空，或者 等于 q ,等于 p，直接返回即可
• 再判断左树中，是否有 p、q 节点
• 再判断右树中，是否有 p、q 节点
• 最后，在进行最终判断
  • 如果左树右树都不为空，则 root 节点就是 最近公共祖先
  • 如果左树为空，右树不为空，则最近公共祖先就是 右树的不为空的节点
  • 如果右树为空，左树不为空，则最近公共祖先就是 左树的不为空的节点
  • 如果两个都为空，直接返回 null

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == q || root == p){
            return root;
        }     
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left != null && right != null){
            return root;
        }else if(left != null && right == null){
            return left;
        }else if(left == null && right != null){
            return right;
        }else{
            return null;
        }
    }
}

---

LeetCode 450 删除二叉搜索树中的节点

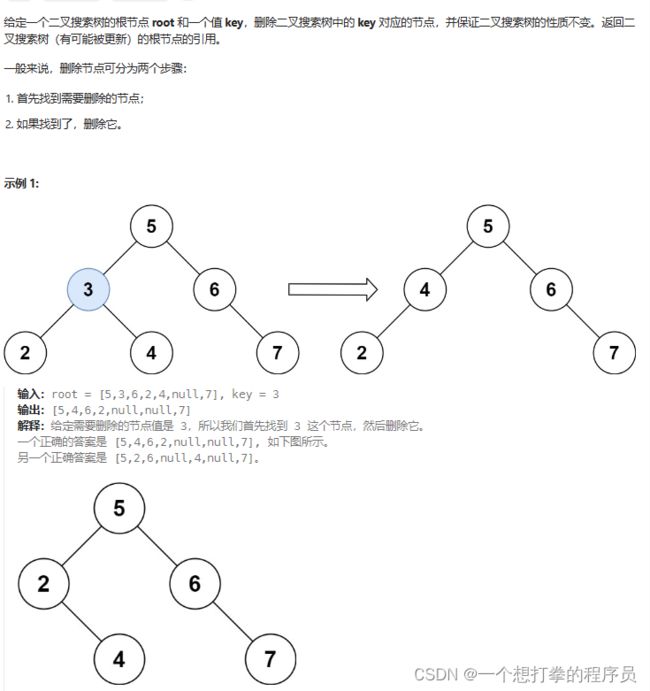
本题思路：删除二叉搜索树中的节点，和在 二叉搜索中插入节点差不多。
判断要删的节点的值和当前节点是否一样，如果一样就删除，不一样，就根据节点值大小，往左或者往右移动。只不过在删除的时候，比较麻烦。

• 首先是递归的出口，如果根节点为空，直接返回 null
• 先处理根节点，如果 根节点的值等于要删除的节点，此时又分为以下几种情况
  • 如果根节点的左树为空，则直接返回根节点的右孩子
  • 如果根节点的右树为空，则直接返回根节点的左孩子
  • 如果都不为空，则往根节点的右孩子的左孩子找，一直找到最小的左孩子
    • 然年让该左孩子的 左孩子为，根节点的左树
    • 根节点更换为根节点的右孩子节点
• 如果节点的值大于根节点，就处理右树，在右树中寻找
• 如果节点的值小于根节点，就处理左树，在左树中寻找

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if(root == null){
            return root;
        }
        if(key == root.val){
            if(root.left == null){
                return root.right;
            }else if(root.right == null){
                return root.left;
            }else{
                TreeNode cur = root.right;
                // 找到该节点右树中，最左边最小的节点
                while(cur.left != null){
                    cur = cur.left;
                }
                // 让最小节点的 left 等于这个节点
                cur.left = root.left;
                root = root.right;
            }
        }
        if(key > root.val){
            // 当前根节点的右树，为在右树上找到删除的节点后，新构造的树
            root.right = deleteNode(root.right,key);
        }
        if(key < root.val){
            // 当前根节点的左树，为在左树上找到删除的节点后，新构造的树
            root.left = deleteNode(root.left,key);
        }
        return root;
    }
}

---

LeetCode 108 将有序数组转换为二叉搜索树

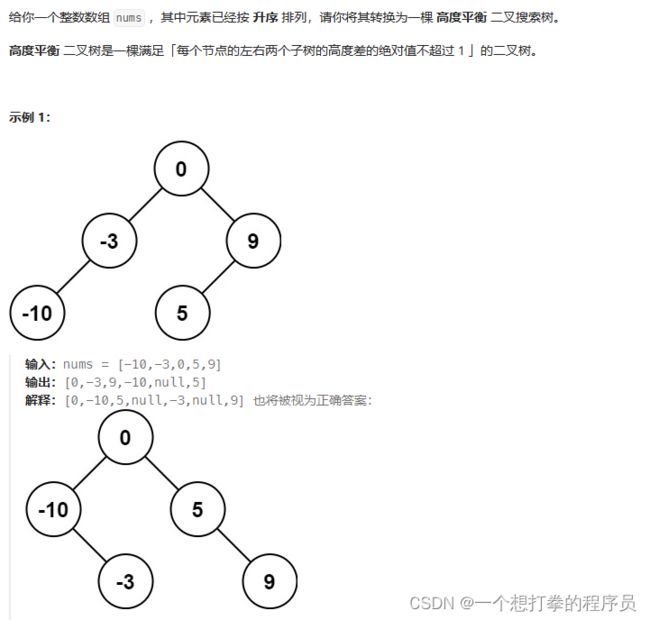
本题思路：利用中序遍历来构造。由于构造的必须是二叉平衡树。所以我们构造的时候，将树均匀分成两份，取中间节点作为根节点，然后更新左中序树，更新右中序树。再递归构造即可！

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return travl(nums,0,nums.length);
    }
    public TreeNode travl(int[] nums, int start, int end){
        if(start == end){
            return null;
        }
        int index = (start + end) >> 1;
        TreeNode root = new TreeNode(nums[index]);
        if(nums.length == 1){
            return root;
        }
        int startleft = start;
        int endleft = index;
        int startright = index + 1;
        int endright = end;
        root.left = travl(nums,startleft,endleft);
        root.right = travl(nums,startright,endright);
        return root;
    }
}

---

LeetCode 669 修剪二叉搜索树

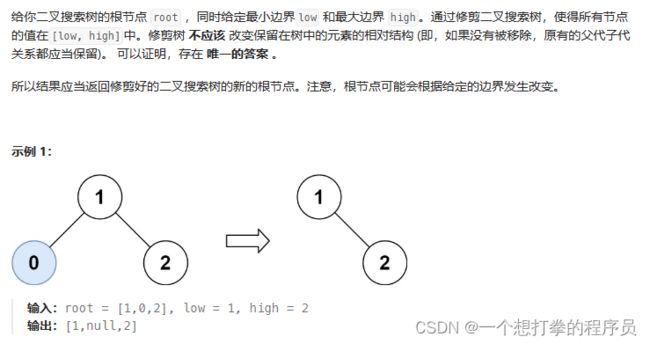
本题思路：判断当前节点的值，是否在区间内，如果不在，不能直接删除，因为它的左树或者右数中可能存在符合的节点！

• 首先找到递归的出口 root == null，直接返回 null
• 如果当前节点小于区间，但是它的右树中，可能存在符合区间内的节点，所以不能直接删除当前节点，需要递归进行 传入该节点的右子树
• 如果当前节点大于区间，但是它的左树种，可能存在符合区间内的节点，所以不能直接删除当前节点，需要递归进行 传入该节点的左子树
• 然后在左树中，删除节点
• 然后在右树中，删除节点

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null){
            return null;
        }
        // 如果当前节点值 小于区间
        if(root.val < low){
            // 此时虽然当前节点值小于 low, 但是它的右树中，可能存在符合区间内的节点，所以不能直接删除当前节点
            return trimBST(root.right,low,high);
        }
        // 如果当前节点值 大于区间
        if(root.val > high){
            // 此时虽然当前节点值大于 high, 但是它的左树中，可能存在符合区间内的节点，所以也不能直接删除
            return trimBST(root.left,low,high);
        }
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}

---

LeetCode 538 把二叉搜索树转换累加树

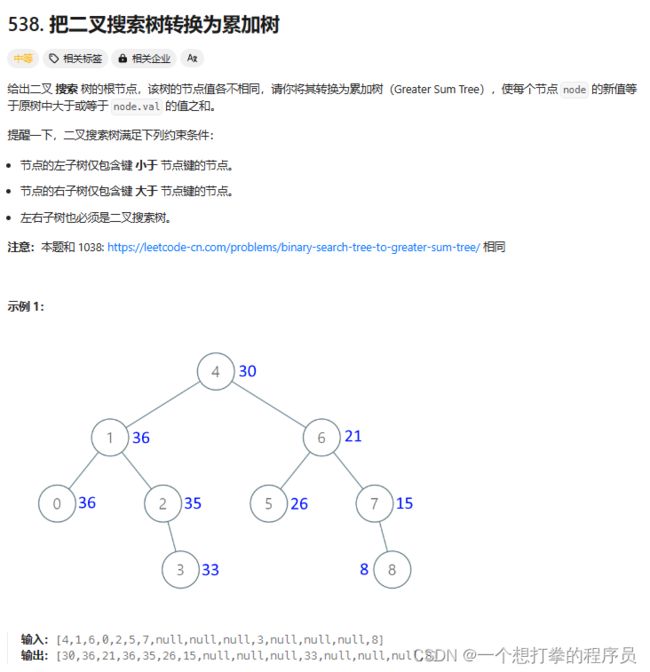
本题思路：可以看出，遍历的顺序是 右 根 左， 我们可以用双指针的操作，来完成累加。 定义一个 pre = 0 ， cur 指向 8 ， 当前的节点值 就等于 cur.val + pre

class Solution {
    int pre = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root == null){
            return null;
        }
        travel(root);
        return root;
    }
    
    public void travel(TreeNode root){
        if(root == null){
            return;
        }
        travel(root.right);
        root.val += pre;
        pre = root.val;
        travel(root.left);
    }
}