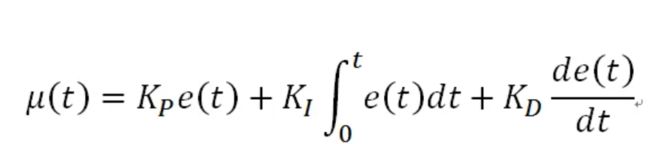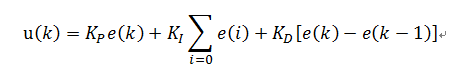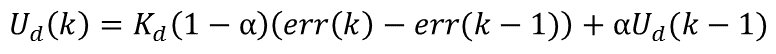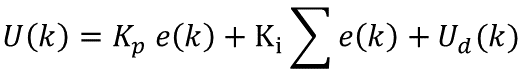PID各种算法的基本优缺点
PID时间系数对PID本身的影响
积分时间过小积分作用增强。
微分时间过大,微分控制作用过强,容易产生振荡。
在这里的时间系统,一般指的是采样的时间,也就是PID控制的周期。在无人机当中一般采用10ms控制一次。
一般来说采样周期越小,数字模拟越精确,控制效果越接近连续控制。
对大多数算法,缩短采样周期可使控制回路性能改善,但采样周期缩短时,频繁的采样必然会占用较多的计算工作时间,同时也会增加计算机的计算负担。
对于变化迅速的,采样周期应适当减小。多回路控制,采样周期应该适当延长,使得有足够的时间控制。
位置式PID
离散化后的公式:
优点:静态误差小,溢出的影响小。
缺点:计算量很大,累积误差相对大,在系统出现错误的情况下,容易使系统失控,积分饱和。
使用:一般需要结合输出限幅和积分限幅使用。积分限幅是避免积分失控的一种手段,也是为了加快调节时间,减少积分饱和的影响,输出限幅是为了使系统输出不过度,也能够减少系统的调节时间,减少超调量。
位置式PID适用于执行没有积分部件的对象。
增量式PID
离散化后的公式:
优点:溢出的影响小,在系统出现错误的情况下,影响相对较小(因为只与过去的三次误差有关),运算量也相对较小。
缺点:有静态误差(因为没有累积误差)。
使用:位置式PID适用于执行有积分部件的对象。
位置式PID和增量式PID
C语言实现:
//积分限幅#define INERGRAL_MAX 200#define INERGRAL_MAX -200//输出限幅#define OUT_MIN -1000#define OUT_MAX 1000// 滤波系数a(0-1)#define PARAMETER 0.01//PID结构体typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int Error2; // Error[n-2]volatile int iError; // Error[n]volatile int Error_sum;} PID/****************************************************************************************/ // 位置式PID// //pwm=Kp*e(k)+Ki*∑e(k)+Kd[e(k)-e(k-1)]/****************************************************************************************/float PID_Postion (int iError,PID* sptr){float iIncpid=0;sptr->iError=iError; // 计算当前误差//sptr->iError=filter(sptr->iError,sptr->Error1); 一阶滤波器sptr->Error_sum+=sptr->iError;//积分项///当输出限幅的时候,积分累加部分也应同时进行限幅,以防输出不变而积分项继续累加,也即所谓的积分饱和过深。//积分量限幅if(sptr->Error_sum >INERGRAL_MAX){sptr->Error_sum = PID_InitStruct->INERGRAL_MAX ;}if(sptr->Error_sum < INERGRAL_MIN){sptr->Error_sum = PID_InitStruct->INERGRAL_MIN ;}iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum // I+sptr->Derivative * (sptr->iError-sptr->Error1); // Dsptr->Error1=sptr->iError; // 存储误差,用于下次计算iIncpid=PID_OutputLimit(sptr,iIncpid);//PID输出限幅return(iIncpid); // 返回计算值}/****************************************************************************************/ //增量式PID// pwm+=Kp[e(k)-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)] ///****************************************************************************************/float PID_increase(int iError,PID* sptr){float iIncpid=0;sptr->iError=iError;//直接检测当前偏差iIncpid=sptr->Proportion * (sptr->iError-sptr->Error1) // P+sptr->Integral * sptr->iError // I+sptr->Derivative * (sptr->iError-2*sptr->Error1+sptr->Error2); // Dsptr->Error2=sptr->Error1; // 存储误差,用于下次计算sptr->Error1=sptr->iError;iIncpid=PID_OutputLimit(sptr,iIncpid);//输出限幅处理return(iIncpid); // 返回增量值}//PID初始化void PID_Init(PID *sptr){sptr->Derivative=0;//Kdsptr->Proportion=0;//Kpsptr->Integral=0;//Kisptr->Error2=0;//第二次误差sptr->Error1=0;sptr->iError=0;sptr->Error_sum=0;//第一次误差}//PID输出限制,根据PWM的输出值进行增量式PID输出限制float PID_OutputLimit(PID *this, double output){if ((int)output < OUT_MIN){output = OUT_MIN;}else if ((int)output > OUT_MAX){output = OUT_MAX;}return output;}//一阶低通滤波器//减少毛刺,//滤波系数。取值范围为0~1, 值越小越稳定,越大越灵敏。使用使需要根据实际情况调整滤波系数//输入:新的采样值//输出:滤波后的值float filter(float value,float new_value){return (1-PARAMETER)*value +PARAMETER*new_value;}
两种针对积分的PID:
主要目的是为了尽可能利用积分的优势,消除静态误差,也同时减少积分的副作用。
使PID控制器的超调量减少,调节时间减少,系统更加稳定。
积分分离式PID
积分分离式PID主要是针对位置式PID的积分,引入判断误差大小条件,是否使用积分项。
优点:
判定误差比较大的时候,取消积分项的,使用PD或者P控制,没有I的控制,这样,超调量和调节时间都会同时减少。当误差比较小的时候,引入积分项,消除静态误差。
缺点:
需要经验来确定判断误差的大小,在什么时候使用积分分离比较合适,也就是误差多大的时候取消积分。
应用:
主要用于消除余差,该方法特别适用于生产设备启动阶段的控制。
C语言实现:PID位置式上面有,这里只需要添加一句判断语句和对积分处理。
无积分分离式的PID:
sptr->Error_sum+=sptr->iError;//积分累加iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum // I+sptr->Derivative * (sptr->iError-sptr->Error1); // D
积分分离式PID:
#includeint index=0;//积分分离标志//积分分离处理if(abs(sptr->iError)> 40) sptr->index=0;else{sptr->index=1;sptr->Error_sum+=sptr->iError;//积分累加}iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * (sptr->Error_sum * index) // I+sptr->Derivative * (sptr->iError-sptr->Error1); // D
变速积分PID
变积分PID我的理解是积分分离式PID的变体,积分分离式PID 积分的的权重是1或者0,而变积分PID积分的权重会动态变化。取决于偏差,偏差越大,积分越慢。
优缺点和积分分离式PID差不多,只不过,这个变速积分PID更加科学。
积分分离式PID:
#include#define I_MAX 40#define I_MIN 5int index=0;//积分分离标志//变积分处理if(abs(sptr->iError)> I_MAX) index=0;else if(abs(sptr->iError)< I_MIN) index=1;else index=(I_MAX - abs(sptr->iError) / (I_MAX - I_MIN);if(index!=0) sptr->Error_sum+=sptr->iError;//积分累加iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * (sptr->Error_sum * index) // I+sptr->Derivative * (sptr->iError-sptr->Error1); // D//变速积分也可以这样处理:更加灵活if(fabs(sptr->iError)> I_MAX) index=0;else if(fabs(sptr->iError)< I_MIN) index=1;else if(fabs(sptr->iError>10&&abs(sptr->iError)<20)) index=0.4;else if(fabs(sptr->iError>30&&abs(sptr->iError)<50)) index=0.8;else index=(I_MAX - abs(sptr->iError) / (I_MAX - I_MIN);
两种针对微分的PID如下:
不完全微分PID
这里针对微分的PID控制算法,是减少微分作用的副作用的一些算法,以便更好地利用微分作用的作用。我们知道,当系统引入微分作用得时候会,引进高频干扰。为了抑制这种干扰,便引入低通滤波器。
这种滤波器得优缺点
优点:
对周期性干扰具有良好的抑制作用
适用于波动频率较高的场合
缺点:
相位滞后,灵敏度低
滞后程度取决于a值大小
不能消除滤波频率高于采样频率的1/2的干扰信号
应用:对于诸如阶跃信号等信号变化很大信号。采用不完全微分能够使得微分作用更为持续平缓。
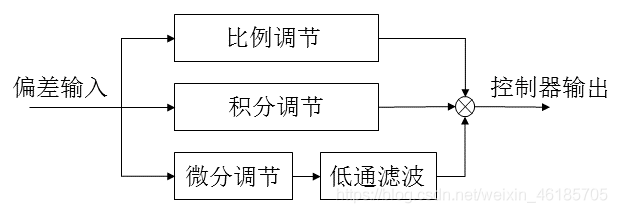
控制图:
位置式PID不完全微分:
公式:
增量式PID不完全微分:
公式:
//PID结构体typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int Error2; // Error[n-2]volatile int iError; // Error[n]volatile int Error_sum;volatile float thisdev;//前一拍时的微分项值volatile float lastdev ;//前一拍时的微分项值float dev_per;//微分系数} PID;//位置式PID不完全微分float PID_Postion (int iError,PID* sptr){float iIncpid=0;sptr->iError=iError; // 计算当前误差sptr->Error_sum+=sptr->iError;//积分项//不完全微分sptr->thisdev=sptr->Derivative*(1-sptr->dev_per)*(sptr->iError-sptr->Error1)+sptr->dev_per*sptr->lastdev;iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum // I+sptr->thisdev; // D//更新值sptr->Error1=sptr->iError;sptr->lastdev=sptr->thisdev;//更新下次微分值return(iIncpid); // 返回计算值}//增量式PID不完全微分float PID_increase(int iError,PID* sptr){float iIncpid=0;sptr->iError=iError;//直接检测当前偏差sptr->thisdev=sptr->Derivative*(1-sptr->dev_per)*(sptr->iError-2*sptr->Error1+sptr->Error2)+sptr->dev_per*sptr->lastdev;iIncpid=sptr->Proportion * (sptr->iError-sptr->Error1) // P+sptr->Integral * sptr->iError // I+sptr->thisdev; // D//更新sptr->Error2=sptr->Error1;sptr->Error1=sptr->iError;sptr->lastdev=sptr->thisdev;//更新下次微分值return(iIncpid); // 返回增量值}
微分先行PID
控制器采用PI控制,将微分作用移动到反馈回路上。微分作用直接对被控量进行微分,对被控量速度进行控制。
优点:在给定值频繁变化的情况下,优先采用微分先行的控制方案能够更迅速的反应,对变化更为敏感。
缺点:更为敏感也就意味着更加不稳定,变化量比较大的情况下,微分作用过分凸显,容易导致超调,引起系统振荡加大。
图示:
对微分部分引入一阶惯性滤波器,进行离散化后的公式:
位置式: 增量式:C语言实现:
//PID结构体//位置式typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int Error2; // Error[n-2]volatile int iError; // Error[n]volatile int Error_sum;volatile float lastPv; //前一拍的测量值volatile float gama; //微分先行滤波系数volatile float derivative;//微分项} PID;//位置式微分先行PIDfloat PID_Postion (float set_point,float processValue,PID* sptr){float iIncpid=0;float temp=0,c1,c2,c3;sptr->iError=set_point-processValue; // 计算当前误差sptr->Error_sum+=sptr->iError;//积分项//微分先行temp=sptr-> gama * sptr-> Derivative+ sptr-> Proportion;//γKp+Kdc3=sptr-> Derivative/temp;//Kd/γKp+Kdc2=(sptr-> Derivative+ sptr-> Proportion)/temp;//Kd+Kp/γKp+Kdc1=c3*sptr-> gama;//γ(Kp/γKp+Kd)sptr-> derivative=c1* sptr-> derivative+c2*processValue-c3* sptr-> lastPv;iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum // I+sptr->derivative; // D//更新值sptr->Error1=sptr->iError;sptr->lastPv=sptr->processValue;//更新下次微分值return(iIncpid); // 返回计算值}//***********************************************************//// 增量式微分先行PID//***********************************************************////增量式PID结构体typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int iError; // Error[n]volatile float lastout; //上一次的测量量volatile float lastout_proinc; //前一拍的过程测量增量volatile float gama; //微分先行滤波系数volatile float out_proinc; //过程测量增量volatile float derivative_inc; //微分项} PID;//增量式PID不完全微分PID_increasefloat PID_increase(float set_point,float processValue,PID* sptr){float iIncpid=0;float temp=0,c1,c2,c3;sptr->iError=set_point-processValue; // 计算当前误差//微分先行out_proinc=processValue-lastout;//这次输出增量temp=sptr-> gama * sptr-> Derivative+ sptr-> Proportion;//γKp+Kdc3=sptr-> Derivative/temp;//Kd/γKp+Kdc2=(sptr-> Derivative+ sptr-> Proportion)/temp;//Kd+Kp/γKp+Kdc1=c3*sptr-> gama;//γ(Kp/γKp+Kd)sptr-> derivative_inc=c1* sptr-> derivative_inc+c2*out_proinc-c3* sptr-> lastout_proinc;iIncpid=sptr->Proportion * (sptr->iError-sptr-> Error1)// P+sptr->Integral * sptr->iError// I+sptr->derivative_inc; // D//更新值sptr->Error1=sptr->iError;sptr->lastout_proinc=sptr->out_proinc;//过程增量更新sptr->lastout=processValue;//上一次的测量量更新return(iIncpid); // 返回增量值}
带死区的PID
死区控制简单理解:
死区,就是到了一个区域,在这个区域内,PID算法不起作用,也就是不做控制。
优势:
可以抑制由于控制器输出量的量化造成的连续的较小的振荡,也就是消除稳定点附近的抖动。这是因为,现实中,总存在误差,一些较小误差难以消除。
缺点:
会造成一定的滞后。设定死区的值也是需要考虑,太小每作用,太大滞后严重。在零点附近时,若偏差很小,进入死去后,偏差置0会造成积分消失,如是系统存在静差将不能消除,所以需要人为处理这一点。
应用:
减少机械磨损,延长设备寿命等。
总结来说:PID调节器中设置死区,牺牲的是调节精度,换来的是稳定性。适用于精度不是很高的系统。
死区的输出为0时,pid控制器的比例部分和微分部分均为0,积分部分保持不变。虽然误差值在死区宽度设置的范围内变化,控制器的输出却保持不变。
C语言实现:
#define DEAD_BAND 50//死区控制值#define PID_OUT_MAX 200 //PID输出上限#define PID_OUT_MAX 200 //PID输出上限#include "math.h"//PID结构体typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int Error2; // Error[n-2]volatile int iError; // Error[n]volatile int Error_sum;} PID/****************************************************************************************/ // 位置式PID// //pwm=Kp*e(k)+Ki*∑e(k)+Kd[e(k)-e(k-1)]/****************************************************************************************/float PID_Postion (float set_point,,float now_point,PID* sptr){float iIncpid=0;sptr->iError=now_point-set_point; // 计算当前误差//死区控制算法if(fabs(sptr->iError)>DEAD_BAND){sptr->Error_sum+=sptr->iError;//积分项iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum // I+sptr->Derivative * (sptr->iError-sptr->Error1); // Dsptr->Error1=sptr->iError ; // 存储误差,用于下次计算}else{iIncpid=0;//sptr->Error_sum+=sptr->iError;//积分项sptr->Error1=sptr->iError; // 存储误差,用于下次计算}return(iIncpid); // 返回计算值}/****************************************************************************************/ //增量式PID// pwm+=Kp[e(k)-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)] ///****************************************************************************************/float PID_increase(int iError,PID* sptr){float iIncpid=0;sptr->iError=iError;//直接检测当前偏差if(fabs(sptr->iError)>DEAD_BAND){iIncpid=sptr->Proportion * (sptr->iError-sptr->Error1) // P+sptr->Integral * sptr->iError // I+sptr->Derivative * (sptr->iError-2*sptr->Error1+sptr->Error2); // Dsptr->Error2=sptr->Error1; // 存储误差,用于下次计算sptr->Error1=sptr->iError;}else{iIncpid=0;//输出增量值为0sptr->Error2=sptr->Error1; // 存储误差,用于下次计算sptr->Error1=sptr->iError;}return(iIncpid); // 返回增量值}
PID梯形积分
积分会有余差,消除不了,为了减少余差,提高运算的精度。便有了PID梯形积分,也能抑制一些随机干扰。
缺点便是,曲线到达设定值的时间会延长。
总的来说:也就积分的作用削弱了。带来的是余差进一步减小。
C语言实现:
typedef struct{volatile float Proportion; // 比例常数 Proportional Constvolatile float Integral; // 积分常数 Integral Constvolatile float Derivative; // 微分常数 Derivative Constvolatile int Error1; // Error[n-1]volatile int Error2; // Error[n-2]volatile int iError; // Error[n]volatile int Error_sum;} PID/****************************************************************************************/ // 位置式PID// //pwm=Kp*e(k)+Ki*∑e(k)+Kd[e(k)-e(k-1)]/****************************************************************************************/float PID_Postion (float set_point,,float now_point,PID* sptr){float iIncpid=0;sptr->iError=now_point-set_point; // 计算当前误差//死区控制算法sptr->Error_sum+=sptr->iError;//积分项iIncpid=sptr->Proportion * sptr->iError // P+sptr->Integral * sptr->Error_sum/2 // 改变的只是这里,多除了2+sptr->Derivative * (sptr->iError-sptr->Error1); // Dsptr->Error1=sptr->iError ; // 存储误差,用于下次计算return(iIncpid); // 返回计算值}
总结
PID的变体还有很多,除了上文,还有专家PID与模糊PID是本文不能承载,也是我不能输出,便作罢。
事物都有两面性,该怎么选择比较合适,怎么将PID的各种变体组合在一起合适自己的系统,这个是需要综合衡量和测试的,要知其然知其所以然。