关于JPEG的那点事儿:JPEG原理篇

前言

本文其实于差不多正好1年前写成，是关于JPEG的那点事儿的补充。但是由于实战篇一直烂尾，拖到现在。前几天看到Google发了个JPEG新算法，说是可以将JPEG的体积同质量情况下再压缩35%，突然想起了这文了。为了说清楚Google为什么能在古老的JPEG上压榨出新的空间，我觉得还是有必要先讲清楚JPEG的原理。但是本文成文之后实在太长，所以我想了想还是把和Google算法相关的、以及一个TL;DR版的JPEG原理单独发文（大概明天8点发w）。另外，前面提到的“实战篇”也会分割放送，减少文章长度。

序言

有一位朋友看了上文后问到，为什么步进（progressive）JPEG可以提高压缩率？

严格来讲，步进（Progressive）和交错（Interlacing，虽然“交错”是最常用的翻译，但是我是在无法完全理解这两个字的汉字想表达啥…）并不是一个概念。要讲步进，得先讲讲交错。

交错指的是图像解码时（以及存储时）并不是按照某个逐个像素依顺序解码——而是采用跳跃的方法：例如将整个图像分割成九个区域，先解码出每个区域的大体形状，然后再逐步解码细节。一般而言，这样的层级解码会分不止2层，例如在PNG使用的Adam7算法中，一共有7个子图像会被存储起来。维基百科上这张图可能会更直观一些：

(From Wikimedia Commons)

这种方式的好处是，在图像加载过程中，图像会由模糊（准确地说是马赛克状）逐渐变清晰，而不是从上到下一行行地显示。这样在图像加载中途读者就可以对图像大概有个概念，而不是只能看到上面完全看不到下面：观感上加载速度会变快，而且也更方便一些。

你肯定要问了，这么做不是相当于在原图上在集成几个不同尺寸的略缩图，体积不增加就不错了，怎么会减小呢？事实上，对于其他图片格式，例如PNG和GIF，如果开启“交错”选项，确实图像会变大。但是对于JPEG的具体实现，所谓的“ progressive”，情况又不太一样。用IJG官方的FAQ里的话说“Basically, progressive JPEG is just a rearrangement of the same data into a more complicated order.”。但是具体技术上的实现方式是什么？

要说清这事儿可能还真得从头说一下JPEG的压缩过程。既然要讲，那就讲的详细一点。接下来我将把JPEG压缩的每个细节步骤（除了DCT的数学原理，这个我真不行……）都讲清楚。如果只是想了解大概，维基百科就写的不错了：但是如果真想做到自己写一个解码编码器的程度，有些细节不厘清还真不行。

JPEG编码基本原理

在DCT之前
JPEG编码主要分成三步，DCT、量化以及无损压缩。不过，在DCT之前，还要先色彩空间转换和色度抽样。色彩空间转换干的就是将RGB转换成YCbCr——即将亮度（Luma）和色度（Chroma）分离开，其理念是人眼对亮度的变化远敏感于色度变化等一大套感知视觉理论，这里不再赘述。顺便一提，色彩空间转换并不是完全无损的——因为转换前后都是整数，自然不可避免会有舍入误差。

转换之后，既然我们知道亮度更敏感，那就有做文章的空间。所谓色度抽样，就是对色度的部分进行抽样/缩小。主流的抽样方法有4:2:2、4:2:0，在JPEG的语境下更多叫做2×1和2×2，前者指水平分辨率抽样一半，垂直不变，后者指水平垂直各抽样一半。完全无抽样的叫做4:4:4，或者1×1。至于具体抽样缩图的算法JPEG里好像没有定义，一般都是直接将相邻两个像素求个平均了事（这里可能会导致图像处理界另一个著名的历史遗留问题：线性vs非线性色彩空间，以后抽空再单独写一下）。

抽样完毕后，终于可以进行到真正的编码部分了。JPEG压缩时，先将原图分割成8×8的block进行编码，又叫“最小编码单元（Minimum Coded Unit，MCU）”。当然，如果你有用色度抽样，MCU的大小也会相应放大。例如，如果你用了4:2:0的抽样，那么MCU就会变成16×16——但是Cr和Cb的实质大小其实依然只有1个8×8，只是塞进去了4个8×8的Y罢了。在编码的时候，每个通道也是分开的，所以这样的MCU可以理解成6个不同的blocks就行（但是压缩完之后的数据顺序又有讲究，后叙）。下面，我用“block”来特指单个通道的8×8的单元，来和MCU区分。

DCT
接下来，我们要对每个block的像素值（8bit图像就是0-255了，接下来全部以最常见的8bit为例。JPEG标准额外支持12bit图像，但是主要用于医疗领域，普通情况极少有人用）进行偏置128之后（使其集中在0两侧，加快DCT运算）做2D DCT转换成频域。转换出的结果依然是一个8×8的矩阵，只不过每个数据点代表的是不同频率（准确地说是一组不同的pattern（见下图））的强度：左上是低频，越往右下越高频。

(From Wikimedia Commons)

所以DCT说白了就是把原图分拆成这些pattern的线性叠加。其中左上角的DC分量，可以近似理解为整个block的强度均值，剩下的则是高频（或称AC）分量。

量化

DCT这步数学上来讲（不考虑舍入误差）是可逆的，真正的有损编码的是下面的量化步骤。量化在这个语境下其实就是拿一个预设的系数矩阵（量化表）去逐一除之前得出的DCT矩阵——介于人类对低频比较敏感，细节可以适当丢失，这个表的原则是越往左上系数越小，越往右下系数越大。至于具体的数据，据说都是实验出来的，不同的软件可能不同。主流的libjpeg根据JPEG标准的推荐，提供了一套0（1？）-100质量分别对应的表，可能也是最常见的系数。当然，你也可以自定义系数，例如Photoshop内置的量化表就和别的软件大多不一样。ImpulseAdventure的作者提供了一份非常详尽的市面上常见软件、相机的内置系数表。表格里数据的总体大小决定了JPEG的质量——系数越大，质量越低。高质量的表可能系数都只有个位数（事实上，100%质量的量化表全是1），而低质量的，例如拿一个JPEG 50%质量的量化矩阵来说，左上角的DC分量的除数有16，而右下区的甚至高达100左右。想象一下去拿这个表去除DCT矩阵，除出来的结果再近似到整数，考虑到右下的高频AC分量本来强度就不高，除以100之后基本都肯定小于0.5了，也就是会被约成0。这么搞下来，整个表就会变成一个右下区几乎都是0，而其他区域数值也很小的矩阵。

Y和Cb/Cr会有不同的量化表（可以猜到，色度那张压缩更狠），这个表会被嵌到JPEG文件的头部中。通过表格的数据可以估算JPEG的当时编码时的质量。

无损压缩

之后就到了无损压缩的部分，也是整个JPEG编码中最麻烦的部分。首先又得学个新词儿——Interleaving。这个一般也翻译成“交错”……但是和上面提到过的Interlacing不是一回事。我们前面知道，每个MCU有少至3个、多至6个8×8的blocks。编码的时候，我们既可以按照MCU分类，一次编码完整个MCU的所有block再进行下一个、也可以采用别的方式，这里按下不表。不过，最常用的、baseline的方法是先按MCU归类，然后按照一个固定的顺序读取。如果是无色度抽样的3 blocks MCU，那就是YCbCr的顺序，如果有多个Y，那就是Y00/Y01/Y10/Y11（左上，右上，左下，右下）/Cb/Cr的顺序。

(From ImpulseAdventure)

这种“不停地在不同components交替取数据编码”的方式（components在这个语境下就是不同的通道，Y、Cb和Cr都分别是一个component）就叫做“interleaving”，这样的JPEG叫做interleaved JPEG。可以看到，绝大部分的baseline JPEG都是interleaved的。

让我们回到每个block里面。首先要将我们的64个分量1D化。我们这里并不是按行或者列的顺序排队，而是通过斜对角蛇形的方式，从左上逐渐跑到右下。

(From Wikimedia Commons)

其原因是：越靠近左上的频率越低，量化压缩之后也越可能不是0，这样排序之后便于下面的游程编码（RLE，run-length encoding）进行。

游程编码

所谓RLE，是一种无损压缩高重复率数据的算法，还是直接引用维基的例子好了：“举例来说，一组资料串”AAAABBBCCDEEEE”，由4个A、3个B、2个C、1个D、4个E组成，经过变动长度编码法可将资料压缩为4A3B2C1D4E（由14个单位转成10个单位）。”

至于JPEG中的实现说起来则比较麻烦。简单概括，对于AC分量，我们只描述非零的强度和他们的位置。具体来讲，就是把非零的coefficient转换成“前置0的数量+强度的比特数”的分类单元+具体强度的形式。而强度是0的AC，自然被包含在那“前置0”里面了。这样说可能太抽象了，举个例子。假设我们的AC1和AC3（分别是矩阵第一行第二排和第三行第一排）分别是-2和3，而AC2是零。那么，AC1就会被表示成

（0，2）（-2）

（0，2）乃是分类单元（categories），0表示前面有0个0（毕竟这是第一个），2表示后面跟的数据（-2）需要用两位（2bit）才能表示（下述）。同理，AC3前面有1个0（AC2），那么就会被表示成

（1，2）（3）

或者我们把前面俩改写成16进制，共同占用1个字节：因为后面的数据不会超过15位（F）（实际上不会超过14位，高位F的部分除了F0特殊定义之外，并用不到），零的数量虽然确实会超过15个，但是我们特别指定（15，0）（0xF0，有的地方称作ZLF，“zero run length”的意思）为用来表示16个连续的0。如果某个block最后部分全是零，可以提前输出（0x00，End-of-Block，EoB，无需跟强度值）来结束这个block。

DC分量处理

对于DC量，首先我们用和前一个block的DC分量的差分的方式来记录——这样做可以节省一部分体积，因为图像大多是连续的，相邻block的DC分量一般相差不大，这么操作可以大幅度降低DC分量（一般是最大的一个数，也需要最多比特）的比特长度。这种编码方式叫做Differential pulse-code modulation。

另外，我们也要像AC一样，对每个强度量先指定其位长的分类单元（否则我们怎么知道读到哪里算完呢？）：0表示该DC量是0、1表示该DC量的数据只有1位、2表示有两位、……直到15（或者F），然后再写我们的数值。例如，如果一个DC量是15，那么就会被表示成

（4）（15）

即（位长）（数据）的形式。因为15需要4位才能编码下（下述），所以是4。

编码为二进制及霍夫曼编码
接下来，我们要进行最后的终极编码，也就是将上面这一堆劳什子转换成二进制。

对于强度的部分，很简单，按照之前分配好的位数转换即可。但是别忘了，我们的数值是有符号整数，要转成无符号的0和1，所以要稍微偏移（shift）一下。如果数据是0，对于AC自然就直接跳过了，DC会被分配“0位”，也就是只有分类单元的部分，而并没有数据。分配1位时，0代表-1，1代表1；分配2位时，用00表示-3、01表示-2、10表示2、11表示3，以此类推。这个编码方式是JPEG标准指定的，所有JPEG都一样，不能自定义。其实，它是用补码（二补数）推算出来的：如果数据是正的，那么就取补码最后N位（位数前面分配了）；如果数据是负的，就取补码最后N位再减一。举例子的话，15被分配4位，15的补码是0…00001111（具体有多少个前置零取决于你的比特数，但是这里不影响），取最后四位就是1111；如果是-15，补码是1…1110001，取最后4位再减一就是0000。到这里也应该看出来了，我们的位数也不是随便分配的，说白了就是对于绝对值处在[2^N, 2^(N+1))之间的数，我们分配N位来表示。具体可以参照这文中的Table 5。

不过对于前面的分类单元部分，则不是直接转换成二进制就算完了，我们要充分利用霍夫曼编码的方法进一步压缩。如果有不了解霍夫曼的，其实就是简单地重排数据编码方式，出现频率高的用更少的比特编码，频率低的用更多的来编码，并最终得到一个总比特数更短的二进制码。如果我们不用霍夫曼，可以看到上面的分类单元对于AC量每个有8位，对于DC也有4位。霍夫曼编码后，其长度变成2至十几位不等。

JPEG默认就是启用霍夫曼的，其标准中也有个推荐的霍夫曼码表。但是和量化表一样，你也可以自定义——事实上，有人就发现，Photoshop就有一套自己单独搞的霍夫曼码表，而且根据JPEG的质量不同还稍有不同，以求达到最佳的压缩效果。另外，DC和AC、Luma和Chroma都可以分别使用不同的霍夫曼表，也就是说一般会有四张霍夫曼表。该表显然也会和量化表一样存在header中，否则无法解码。

不过，最优的霍夫曼（在JPEG文件结构的限制内。有研究称JPEG的霍夫曼从设计上就不可达到最优）自然是对于每个JPEG单独统计每个分类单元出现频率然后构建霍夫曼表了：——这也就是一般软件保存JPEG时的“优化霍夫曼”或者“Optimize”的意思了。不过很显然，这样做会要求先对所有MCU进行一遍扫描，自然会降低编码速度（也需要更大的buffer，这点在设计encoder的时候需要注意）。

最后，这些纯二进制的数据会按照MCU1-Y-DC、MCU1-Y-AC、MCU1-Cb-DC、MCU1-Cb-AC、MCU1-Cr-DC、MCU1-Cr-AC、MCU2-Y-DC……的顺序拼在一起。整个数据块必须结束在整字节里，最后不足的部分补1。另外一个特殊之处在于，如果数据中某个字节出现了0xFF（1111 1111），为了防止和JPEG的marker（标示各个组成部分开始的标示）混淆（全部以x0FF+非0字节组成），会加入padding 0来改写成0xFF00。

讲到现在，终于把普通的baseline、sequential的JPEG编码原理讲完了。

Baseline？Sequential？
插播一段：关于“baseline”的定义，其实非常含糊。根据ITU的standard的术语表，baseline其实是和“extended”相对应的，而不是progressive——sequential才是。“extended”是指每次Scan（下述）可以有高达8张霍夫曼表、并且每个component的可以是12位等等的扩展格式（极为罕见）。但是，在统一标准中后文中又出现了baseline和progressive的相对应……总而言之，连ITU自己的文档里术语都不是很严谨。在民间使用时，baseline多用来和progressive相对（虽然sequential更合适一点），这点要搞明白。

步进（Progressive）JPEG
我们还完全没提到最重要的步进（progressive）到底是怎么回事。不过看到上一段我们应该能想到，由于DCT的特性，高低频的数据都已经分离出来了。如果我们在存储时并不是按照完全按照MCU的顺序，而是先把DC和一些序号较小的AC分量挑出来先存储，这样加载的时候不就可以做到从模糊到清晰的效果了吗？没错，这就是progressive JPEG的基本原理了。而且，这样做我们只是调整了同样数据的位置而已，理论上并不会增加体积。

在具体实现上，得先讲一下Scan的概念。JPEG中经过DCT和量化之后的那堆系数（就是那些8×8矩阵），可以分为多成多个Scan来保存——每个Scan中只分配、存储部分数据。具体的分配方式，可以分为三种：

按照component分开。还记得上面提过的interleaved的概念吗？一般的JPEG，是将三个components（Y、Cb、Cr）全部混在一起编码的。你也可以全部分开——每个Scan只处理一个component。
按照8×8 block中的序列号（依然是蛇形顺序）分开。
按照编码后（二进制）的强度量的比特位置分开。
其中，后两个又称作“progression”，采用这种方式来分scan的JPEG就是progressive scan了。

Spectral selection
采用第2种方式的，叫做“Spectral selection”。例如，我们可以单独压缩0（DC），然后是AC1-AC6，然后剩下的AC7-63再一起。这样在传输图像时，DC部分在第一个scan就会扫描到，后面的慢慢读取。不过具体分配方式并不是任意的，有以下规定（ITU T.81 G.1.1.1.1）：1）DC和AC必须分开；2）只有DC的Scan可以是interleaved（包含多个components，也就是色度亮度一起编码），AC的Scan必须是只含有一个component。所以，更现实的分配方式可以是

、

AC scans:

0: 1-2, 0, 0 ; # First two Y AC coefficients
0: 3-5, 0, 0 ; # Three more
1: 1-63, 0, 0 ; # All AC coefficients for Cb
2: 1-63, 0, 0 ; # All AC coefficients for Cr
0: 6-9, 0, 0 ; # More Y coefficients
0: 10-63, 0, 0 ; # Remaining Y coefficients

这个范例引用自 libjpeg-turbo的wizard.txt，这也是cjpeg.exe支持的scan file的格式。其中的0,0部分，下面马上提到。

Successive approximation
采用第3种的，叫做“Successive approximation”（有的地方叫做Successive renement，而把两者共用叫做Successive approximation……没错就是这么混乱）——所谓按照比特位置，就是把每个分量系数（coefficient）的二进制强度（或者称值）按照高位低位分开。例如，假设我们的值都是8 bit，我们可以在第一次scan只传输前7位，最后一次scan再把最低一位（Least significant bit，LSB）传输——可想而知，其效果就是图片精度逐渐变高了。上图的0,0部分的意思就是没有successive approximation。

这么说可能还是觉得有点迷茫，ITU T.81标准中的这张图可能是最直观的了：

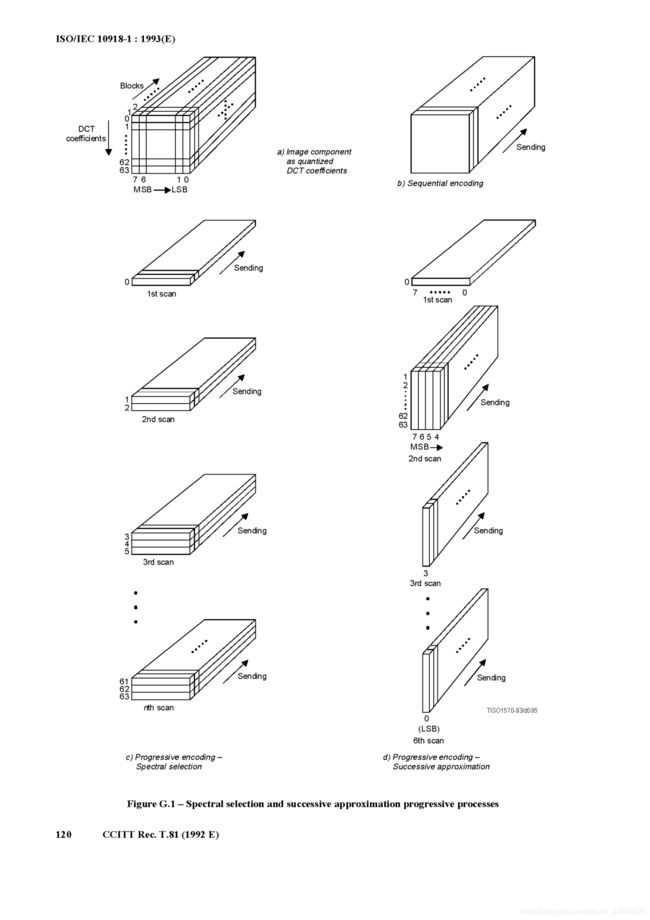
可以看出，整个过程有高达10个Scan。第一个Scan输送所有component的DC分量（除了最后一个bit，即LSB）；然后输送Y通道的前5个AC分量，不过不包含最后两个bit；接下来是Chrma的所有AC分量，但是不包含最后一个bit（如上所述，在progressive中除了DC分量其他的都不允许interleaving，所以分了两次scan；而且，这里选择了先scan了Cr，因为人眼对Cb最不敏感）。再接下来是Y通道的后面6-63个AC分量，依然不包含最后两个bit。再下来是Y通道所有AC分量（1-63）的倒数第二个bit。

最后4个scan就是重复上面的顺序将所有的通道、分量的最后一个bit给传送了。

其他细节
至于在具体实现方式上，Spectral selection倒是蛮好理解的，每处理到某个MCU只要只处理其中一部分分量就是了。但是由于每次Scan现在只含有

少数几个分量，对于编号比较大的的高频（例如：6-63）可能会有大量block完全是0。为了进一步节省字节，在EOB的基础上，我们又重新定义了一组EOBn控制符，来表示之后n个block都是空（纯0）的。当然这些控制符也会被霍夫曼编码了，就像EOB和ZLF一样。

Successive approximation说起来就有点复杂了。如果上面的scan file有仔细看，就会发现每个部分（DC或者每个component的AC）第一次Scan发送的比特数不一，但是之后每次Scan都只输送一个bit。这也是JPEG的规定。对于DC，很容易理解：假设我们某个MCU的某个component是7好了，那么二进制就是111，三位。如果我们分成两次Scan，第一次只传送前两位——也就是11，那么很显然，其“分类单元”应该是0x02；在第二次Scan的时候，因为很显然只有一位，那么分类单元那部分就可以省略掉了，直接把最后的bit补齐即可。

结语

那么，回到最开头的问题，为什么用progressive模式，就会体积减小呢？这里我没有一个确定的答案（…），但是可以看到，和DC/AC全部interleave在一起的Sequential模式相比，其最大的优势是把各个MCU的相似的分量都排在了一起；可以想到，这么做绝对有利于含有预测性质的游程编码，乃至后面的霍夫曼编码。另外，单纯把数据分成好几份（好几个Scan）然后设定不同的霍夫曼表这件事本身可能就能提升不少效率。