2-5基础算法-双指针/二分

一.双指针

这里是用两个变量来表示（数组）下标，并非真的指针
（一）对撞指针
两个指针left、right（简写为l,r)分别指向序列第一个元素和最后一个元素。然后l指针不断递增，r不断递减，直到两个指针的值相撞或错开（即l>=r)，或者满足其他要求的特殊条件为止。

对撞指针一般用来解决有序数组或者字符串问题（常见于区间问题）：查找有序数组中满足某些约束条件的一组元素问题：比如二分查找、数字之和等问题。字符串反转问题：反转字符串、回文数、颠倒二进制等问题。

[例] 回文判定

评测系统

采用对撞指针，每次判断s[l]和s[r]是否相等

#include 
#include 
#include 
using namespace std;
const int N = 1e6 + 5;
int main() {
	char a[N];
	cin >> a;
	int l = 0, r = strlen(a)-1;
	while (l < r) {
		if (a[l] != a[r]) {
			cout << "N";
			return 0;
		}
    l++;
    r--;
	}
	cout << "Y";
}

也可以采用常规的方法，和它的反转串字符比较

#include 
#include 
#include 
using namespace std;
int main() {
	string s1, s2;
	getline(cin, s1);
	s2 = s1;
	reverse(s1.begin(), s1.end());
	if (s1 == s2) {
		cout << "Y";
	}
	else {
		cout << "N";
	}
}

（二）快慢指针
两个指针从同一侧开始变量，且移动的步长不同

[例1] 美丽的区间

评测系统

暴力方法有三个测试用例超时，复杂度O(n²)

#include 
#include 
#include 
#include 
using namespace std;
const int N = 1e5 + 5;
int main() {
	int n, S;
	int a[N];
	cin >> n >> S;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	int ans = n + 1;//记录最小区间长度
	for (int l = 0; l < n; l++) {
		int sum = 0;
		for (int r = l ; r < n; r++) {
			sum += a[r];
			if (sum >= S) {
				ans = min(ans, r - l + 1);
				break;
			}
		}
	}
	cout << (ans > n ? 0 : ans);
}

优化，复杂度O(n)
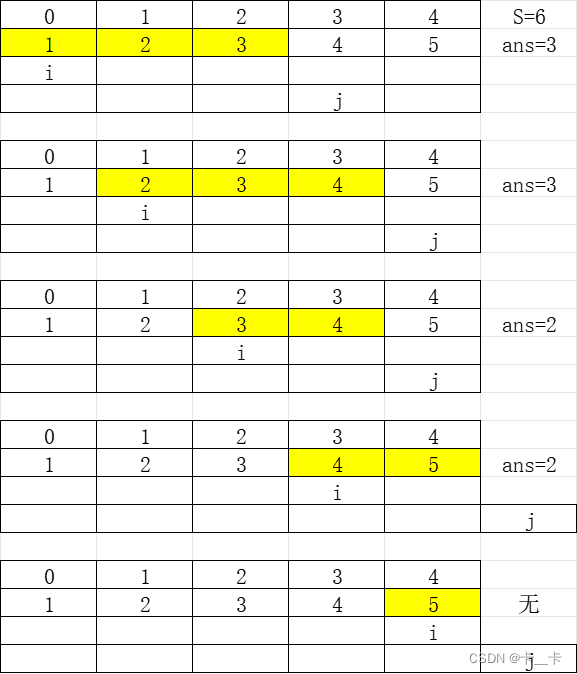
在指定窗口内从左到右寻找满足要求的区间，然后滑动窗口找到最优解。
i表示滑动窗口的左边界，j往后更新，当到达末尾或sum≥S后停止（因为再往后区间只会更大）。接下来滑动窗口后移（i++），为避免sum的重复计算，只需减去a[i]的值即可完成滑动窗口的更新，整个过程中j不回溯。

#include 
#include 
#include 
#include 
using namespace std;
const int N = 1e5 + 5;
int main() {
	int n, S;
	int a[N];
	cin >> n >> S;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	int ans = n + 1;//记录最小区间长度
	int sum = 0, j = 0;
	for (int i = 0; i < n; i++) {
		while (j < n && sum < S) {
			sum += a[j++];
		}
		if (sum >= S) {
			ans = min(ans, j-i);
		}
		sum -= a[i];
	}
	if (ans == n + 1) {
		ans = 0;
	}
	cout << ans;
}

[例2] 挑选子串

评测系统

找到一个合适的子串后，再往后新增元素，一定满足要求。

j 回溯时

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int main() {
	int n, m, k;
	int a[N];
	cin >> n >> m >> k;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	int sum = 0;
	for (int i = 0; i < n; i++) {
		int num = 0;
		int j = i;
		while (j < n) {
			if (a[j] >= m) {
				num++;
			}
			if (num == k) {
				sum += n - j;
				break;
			}
			j++;
		}
	}
	cout << sum;
}

一种更高效的方法，j 不回溯

#include 
#include 
using namespace std;
const int N = 1e5 + 5;
int main() {
	int n, m, k;
	int a[N];
	cin >> n >> m >> k;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	int sum = 0;
	int j = 0, num = 0;
	for (int i = 0; i < n; i++) {
		//int num = 0;
		//int j = i;
		while (j < n && num < k) {
			if (a[j] >= m) {
				num++;
			}
			j++;
		}
		if (num == k) {
			sum += n - j + 1;
		}
		if (a[i] >= m) { //左端被移除的元素是大于等于m的
			num--;
		}
	}
	cout << sum;
}

（三）练习
1.聪明的小羊肖恩


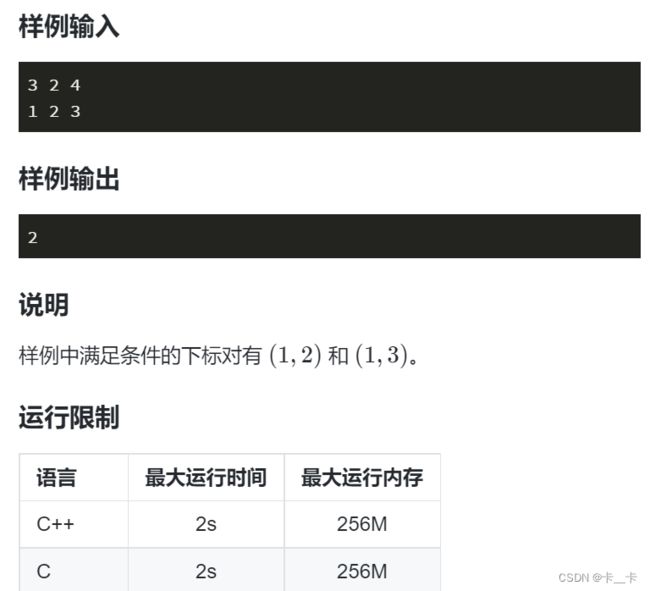
暴力方法会超时
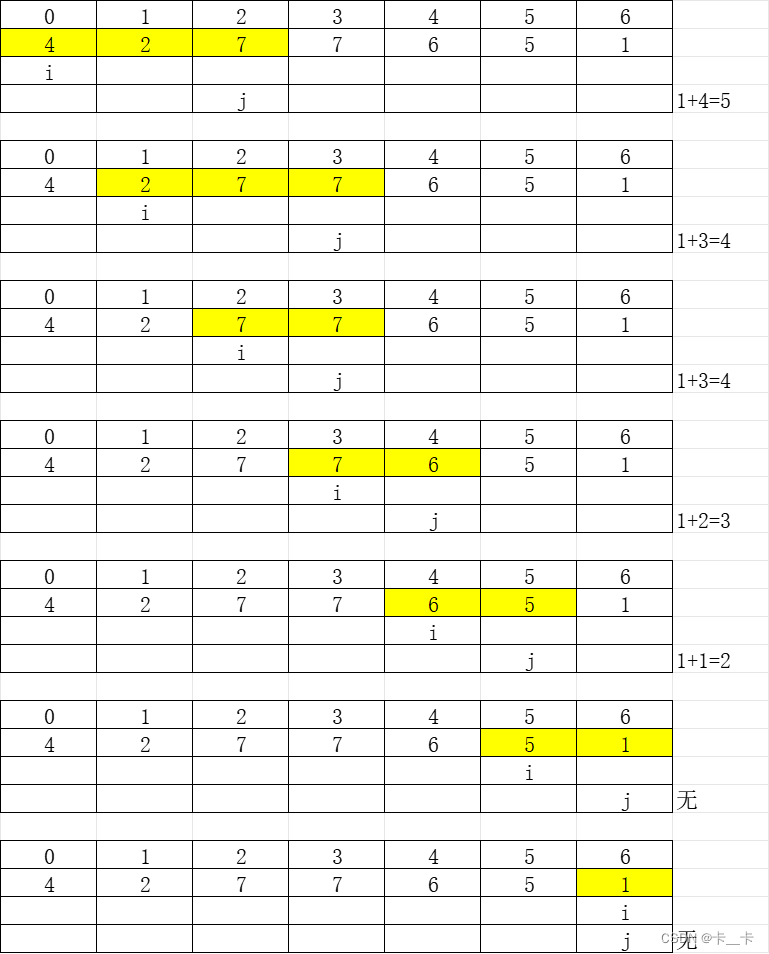
设a[i]+a[j]=sum
设sum≤R的下标组合数量为y，sum≤L-1的下标组合为x，则所求为y-x
我们可以抽象成求解sum≤Z的问题，分别带入R和L-1即可

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int a[N];
int n, L, R;
long long lessz(int z) {  //必须long long
	long long num = 0;  //必须long long
	int left = 1, right = n;
	while (left < right) {
		while (left<right && a[right] + a[left] > z) {
			right--;
		}
		num += right - left;
		left++;
	}
	return num;
}
int main() {
	cin >> n >> L >> R;
	for (int i = 1; i <= n; i++) {
		cin >> a[i];
	}
	sort(a + 1, a + n + 1);
	long long sum = lessz(R) - lessz(L - 1);  //必须long long
	cout << sum;
}

2.神奇的数组

评测系统

分析：两个二进制数相加时如果没有产生进位，那么此时两个数异或的值等于相加的值，该性质推广到多个数也成立。所以对于一个神奇数组来说，每一个比特位它都最多只有一个数可以在该位为1
假设区间 [l,r]=是满足条件的，显然区间 [l,l]，[l,l+1]，[l,l+2]…[l,r-1]也一定满足条件
两次异或又回到原数
（表中num表示每轮的值）

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int main() {
	int a[N];
	int n;
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	int left = 0, right = 0;
	int yihuo=0;
	long long num=0;
	while (left < n) {
		while (right < n&&((yihuo^a[right]) == (yihuo+a[right]))) {
			yihuo = yihuo ^ a[right];//或yihuo = yihuo + a[right];
			right++;
		}
		num += right - left;
		yihuo = yihuo ^ a[left];//移除左端点
		left++;
	}
	cout << num;
}

二.二分

（一）简介
二分法是一种高效的查找方法，它通过将问题的搜索范围一分为二（两边具有明显的区别），迭代地缩小搜索范围，直到找到目标或确定目标不存在。二分法适用于有序数据集合，并且每次迭代可以将搜索范围缩小一半。
（二）整数二分
终止条件是l和r相邻

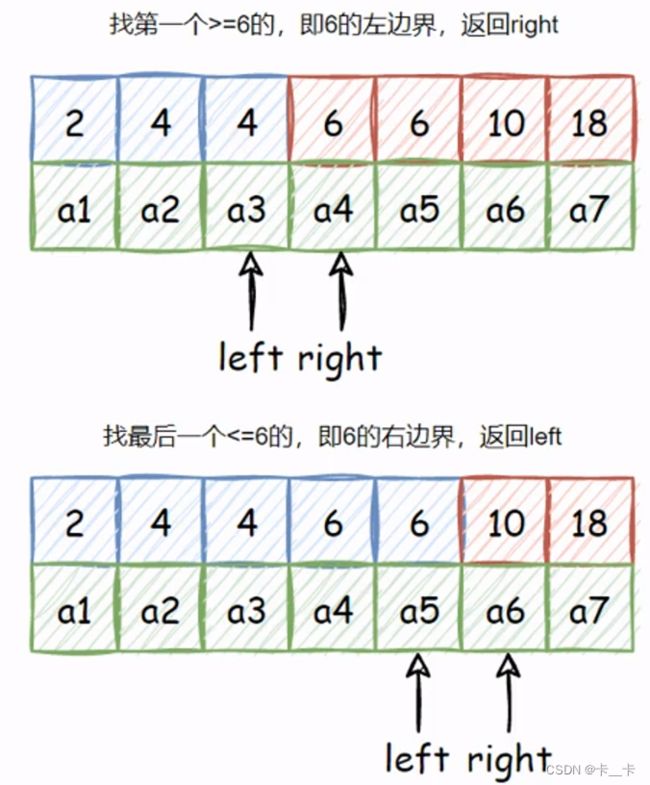
[例] 二分查找数组元素


评测系统

按照1-2节第3条的方法可以解决

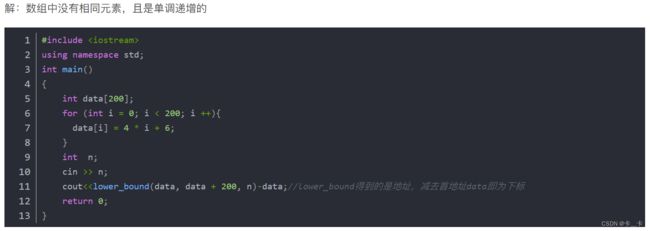
如果以r作为答案输出，区间应该在[l+1,r]，即[0,199]，即l=-1，r=199
如果以l作为答案输出，区间应该在[l,r-1]

#include 
#include 
using namespace std;
int main() {
	int data[200];
	for (int i = 0; i < 200; i++) {
		data[i] = 4 * i + 6;
	}
	int n;
	cin >> n;
	//cout<
	int l = -1, r = 199;
	while (l + 1 != r) {
		int mid = (l + r) / 2;
		if (data[mid] >= n) {
			r = mid;
		}
		else
			l = mid;
	}
	cout << r;
}

（三）浮点二分
在实数范围内查找，l和r几乎指向同一位置时停止

int main() {
	double l = 0, r = 1e9, eps = 1e-6;
	while (r - l >= eps) {//二者足够接近，几乎重合
		double mid = (l + r) / 2;
		if (f(mid) >= 0) {
			r = mid;
		}
		else
			l = mid;
	}
	cout << r;
}

（四）二分答案

[例1] 跳石头

评测系统

如果我们已知最短跳跃距离，可以推出应该搬走多少块石头
最短跳跃距离（mid）越大，需要搬走的石头就越多（满足单调）
我们把最短跳跃距离作为二分的数组，查看是否可以搬走当前数量的石头

注：第一块石头不一定在起点，同时我们不能移走在起点和终点的岩石，但若不在起点和终点，第一个和最后一个岩石可能被移除。

#include 
#include 
using namespace std;
const int n = 5e4 + 5;
int a[n] = { 0 };
int L, N, M;
int check(int mid) {
	int num = 0,last=0;//last为左端点石头下标
	for (int i = 1; i <= N; i++) { //i=1表示第一块岩石可能移除，如果在起点，按程序逻辑不可能被移除
		if (a[i] - a[last] < mid) {
			num++;
			continue;
		}
		last = i;
	}
	if (L - a[last] < mid) { //防止最后一块被移走，需要单独说明
		return M + 1;//返回一个大于M的数使判断不成立
	}
	return num;
}
int main() {
	cin >> L >> N >> M;
	for (int i = 1; i <= N; i++) { //下标必须从1起，留出a[0]表示起点
		cin >> a[i];
	}
	int left = 0, right = 1e9 + 5;//最小跳跃距离可能比N大
	while (left + 1 != right) {
		int mid = (left + right) / 2;
		if (check(mid) <= M) {  //mid是最小跳跃距离
			left = mid;
		}
		else
			right = mid;
	}
	cout << left;
}

[例2] 肖恩的苹果林

评测系统
类似上题，我们考虑移除部分坐标

#include 
#include 
using namespace std;
const int n = 1e5 + 5;
int N, M;
int a[n] = { 0 };
int check(int mid) {
	int num = 0, last = 1;
	for (int i = 2; i <= N; i++) {//此题没有左右端点，从第一个坐标和第二个坐标之间的差值开始判断即可
		if (a[i] - a[last] < mid) {
			num++;
			continue;
		}
		last = i;
	}
	return num;
}
int main() {
	cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		cin >> a[i];
	}
	sort(a + 1, a + 1 + N);//确保升序排列
	int left = 0, right = 1e9 + 5;
	while (left + 1 != right) {
		int mid = (left + right) / 2;
		if (check(mid) <= (N - M)) {
			left = mid;
		}
		else {
			right = mid;
		}
	}
	cout << left;
}

当然也可以正向考虑，mid（最小距离）越小，能种的树就越多

#include 
#include 
using namespace std;
const int n = 1e5 + 5;
int N, M;
int a[n] = { 0 };
int check(int mid) {
	int num = 1, last = 1;//num从1开始，第一个位置一定能种，然后考虑后面的间隔
	for (int i = 2; i <= N; i++) {
		if (a[i] - a[last] < mid) { //距离不满足，跳过
			continue;
		}
		num++;
		last = i;
	}
	return num;
}
int main() {
	cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		cin >> a[i];
	}
	sort(a + 1, a + 1 + N);//确保升序排列
	int left = 0, right = 1e9 + 5;
	while (left + 1 != right) {
		int mid = (left + right) / 2;
		if (check(mid) >= M) { //check返回最多能种多少棵数
			left = mid;//注意这里是负相关，mid越小，能种的树就越多。（若正相关上面if应该是≤）
		}
		else {
			right = mid;
		}
	}
	cout << left;
}

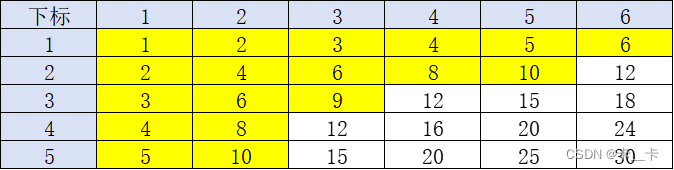
[例3] 肖恩的乘法表


评测系统

在这个5×6的数组中，小于等于10的数=6+5+3+2+2=min(6,⌊10/1⌋)+min(6,⌊10/2⌋)+min(6,⌊10/3⌋)+min(6,⌊10/4⌋)+min(6,⌊10/5⌋)
即在n×m的数组中，小于等于x的元素个数= $\sum _{i=1}^{n}min(m,\lfloor x/j\rfloor )$

我们用rank(x)表示在数组中小于等于x的元素个数，若有rank( l ) < k ≤ rank( r )，则rank( r )即为所求
如l=9，r=10，k=10，rank(9)=16，rank(10)=18，k是所有元素中第

二分查找通过迭代地缩小搜索范围来查找第k大的元素。left和right定义了当前搜索的范围，而mid代表当前范围的中间值。我们在每一步都检查中间值mid是不是第k大的元素。

#include 
#include 
using namespace std;
long long n, m, k;
long long check(long long mid) {
	long long num = 0;
	for (int i = 1; i <= n; i++) {
		num += min(m, mid / i);
	}
	return num;
}
int main() {
	cin >> n >> m >> k;
	long long left = 0, right = 1e14; //注意right的大小取决于m×n
	while (left + 1 != right) {
		long long mid = (left + right) / 2;
		if (check(mid) >= k) {
			right = mid;
		}
		else {
			left = mid;
		}
	}
	cout << right;
}

（五）练习
1.可凑成的最大花束数

评测系统

分析：假设答案为x，我们总共需要的花朵数为kx，每位追求者最多能提供的花朵数为min(ai,x)。条件需满足$\sum _{i=1}^{n}min(ai,x)\ge kx$。为防止kx超过long long上限，我们改为除法

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int n, k;
long long a[N];
double check(long long x) {
    double res = 0;
    for (int i = 0; i < n; i++) {
        res += min(a[i], x);
    }
    return res / x;
}
int main() {
    cin >> n >> k;
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
    }
    long long left = 0, right = 2e14+5;
    while (left + 1 != right) {
        long long mid = (left + right) / 2;
        if (check(mid) >= k)
            left = mid;
        else
            right = mid;
    }
    cout << left;
}

2.最大通过数

评测系统

分析：
（1）必须按顺序通过两个入口的关卡，所以不能排序
（2）单步贪心（按顺序每次选择最小的水晶）不一定是全局最优解
如：水晶7
a[]=2,2,2,2,2
b[]=3,1,1,1,1
单步贪心：2,2,2 共3关
全局：3,1,1,1,1 共5关
（3）我们需要遍历左侧（a）通过的关卡数（x），计算出此时可分配给右侧（b）的水晶，利用二分法求出y
为了高效，可以采用前缀和

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int n, m, k;
long long a[N];
long long b[N];
long long pre1[N] = { 0 };
long long pre2[N] = { 0 };
int main() {
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= m; i++) {
        cin >> b[i];
    }
    for (int i = 1; i <= n; i++) {  //前缀和
        pre1[i] = pre1[i - 1] + a[i];
    }
    for (int i = 1; i <= m; i++) {  //前缀和
        pre2[i] = pre2[i - 1] + b[i];
    }
    int ans = 0;//存放结果
    for (int x = 0; x <= n; x++) { //遍历左侧能通过的关卡数
        if (pre1[x] > k)//如果累积到当前关卡超过了最大水晶数,跳出
            break;
        long long left = 0, right = m+1;//求y
        while (left + 1 != right) {
            long long mid = (left + right) / 2;
            if (pre2[mid] <= k - pre1[x])//k - pre1[x]为剩余可用水晶数
                left = mid;
            else
                right = mid;
        }
        int y = left;
        ans = max(ans, x + y);
    }
    cout << ans;
}

也可以优化前缀和求解和使用upper_bound
upper_bound 使用二分搜索算法来快速定位元素，所以它要求元素已经是排序好的。返回第一个严格大于给定值的元素

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
int n, m, k;
long long a[N];
long long b[N];
int main() {
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] = a[i - 1] + a[i];//优化
    }
    for (int i = 1; i <= m; i++) {
        cin >> b[i];
        b[i] += b[i - 1];//优化
    }
    int ans = 0;
    for (int x = 0; x <= n; x++) { 
        if (a[x] > k)
            break;
        int y = upper_bound(b, b + m + 1, k - a[x]) - b - 1;//优化
        ans = max(ans, x + y);
    }
    cout << ans;
}

3.妮妮的月饼工厂

评测系统

#include 
#include 
using namespace std;
const int N = 1e5 + 5;
long long n, k;
long long a[N];
long long check(long long mid) {
    long long num = 0;
    for (int i = 0; i < n; i++) {
        num += a[i] / mid;
    }
    return num;
}
int main() {
    cin >> n >> k;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    long long left = 1, right = 1e9 + 5;
    while (left + 1 != right) {
        long long mid = (left + right) / 2;//mid表示当前高度
        if (check(mid) >= k) {//check表示当前高度能做多少月饼
            left = mid;
        }
        else {
            right = mid;
        }
    }
    if (check(left) < k) {
        cout << "-1";
    }
    else
        cout << left;
}

4.基德的神秘冒险


评测系统

分析：2421可以先排序，得到1224设为a数组，排列组合为
124（第一个2）
124（第二个2）
122
224
可以看出
固定1，后面可选的数量为C[n-1,2]=3个
固定2，后面可选的数量为C[n-2,2]=1个
想找到第k小的元素，前面至少有k个数，我们希望找到最小的i满足等式C[n-1,2]+C[n-2,2]+…+C[n-i,2]≥k（i从1起）
（ 若i从0起应该加到C[n-1-i,2] ）
若k=2，则a[0]=1（第一个数）对应C[n-1,2]有3个，则输出1
故a[i]即为所求

为了提高效率，可以使用前缀和数组pre，找到最小的i使得pre[i]≥k

#include 
#include 
using namespace std;
const int N = 3e5 + 5;
long long n, k;
long long a[N];
long long pre[N];//前缀和
int main() {
    long long n, q;
    cin >> n >> q;
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    sort(a, a + n);
    for (int i = 0; i < n; i++) {
        pre[i] = (n - i - 1) * (n - i - 2) / 2;  //表示c[n-1-i,2]
        if (i > 0) {
            pre[i] += pre[i - 1];//第二项起累加
        }
    }
    while (q--) {
        cin >> k;
        //lower_bound用于在已排序的范围内寻找不小于给定值的第一个元素
        cout << a[lower_bound(pre, pre + n, k) - pre] << endl;
    }
}

5.体育健将

评测系统

分析：最后一个项目只耗时ai分钟，其余项目都要消耗ai+bi分钟，我们枚举每个项目作为最后一个项目，再看剩余项目最多可以参加几个项目（二分）。这里可以采用谈心策略，每次优先选择ai+bi最小的项目，可以进行排序。
为了高效处理，采用了前缀和
注：数组下标从1开始，输出结果为left；从0开始，输出结果为right

#include 
#include 
using namespace std;
const int N = 2e5 + 5;
long long n, k;
long long a[N];
long long b[N];
long long c[N];//存放ai+bi
long long s[N];//存放c的前缀和
long long check(long long mid, long long i) {
    if (mid < i) {
        return s[mid];
    }
    else {
        return s[mid] - c[i];//mid≥i时，i的时间已被算入，应减去
    }
}
int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++) {
        cin >> b[i];
        c[i] = a[i] + b[i];
    }
    sort(c, c + n);
    for (int i = 1; i <= n; i++) {
        s[i] = s[i - 1] + c[i];
    }
    long long ans = 0;
    for (int i = 1; i <= n; i++) {
        if (a[i] > k)
            continue;
        long long residue = k - a[i];
        long long left = 0, right = n;
        while (left + 1 != right) {
            long long mid = (left + right) / 2;
            if (check(mid, i) <= residue)//判断mid和i的关系
                left = mid;
            else
                right = mid;
        }
        if (left < i)//停止指针在i左侧，结果应加上i这个项目（+1）
            ans = max(ans, left + 1);
        else//停止指针在i右侧，已包括i
            ans = max(ans, left);
    }
    cout << ans;
}