现代计算机图形学入门(二)——变换
文章目录
- 一、模型变换(Model Transformation)
- 二、视图变换(View transformation)
- 三、投影变换(Projection transformation)
-
- 1.正交变换(Orthographic projection Transformation)
- 2.投影变换(Perspective projection Transformation)
- 四、视口变换(Viewport Transformation)
- Reference
在三维空间中,图像上的点最终对应到摄像机的屏幕上要经过四个变换,由于一开始我们的坐标系是定义在图形上的,因此我们要先通过模型变换建立三维世界下的坐标系,将所有图形的坐标都统一起来,然后通过视图变换将世界坐标系的原点移动到摄像机的位置,然后再通过投影变换将远景投射到摄像机的屏幕面上,最后再通过正交变换将投影得到的图像规格化为[-1,1]的正方形大小,这就是整个变换的过程。
一、模型变换(Model Transformation)
在三维空间中,我们也可以用矩阵来表示三维空间的变换,他同样可以表示线性变换和仿射变换,其中最下面一行仍然为(0,0,0,1),最右边一列仍然表示平移的距离:
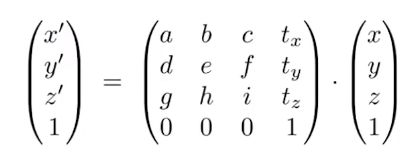
三维空间的缩放:

三维空间的平移:

三维空间中最复杂的操作应该是旋转了,我们首先认定三维空间的旋转是绕着任意轴进行的,那么就会有绕着x轴,y轴和z轴的旋转:


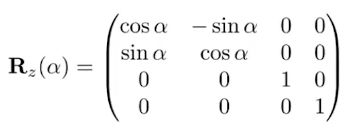
要注意的是绕y轴旋转的sinα部分是反的,这是因为我们的右手系建立都是按着x☞y☞z的顺序来的,但是在利用叉乘生成y轴的时候,我们发现是由z到x生成的,所以导致sinα部分是负的。
//绕Z轴旋转的变换矩阵
//传入旋转角度
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
//初始化model为单位矩阵,Identity()函数会生成单位矩阵
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
Eigen:Matrix4f rotate;
//将角度转换为弧度
float rotation = rotation_angle / 180 * MY_PI;
//按照z轴进行旋转
rotate << cos(rotation), -1 * sin(rotation), 0, 0,
sin(rotation), cos(rotation), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
//
model = model * rotate;
return model;
}
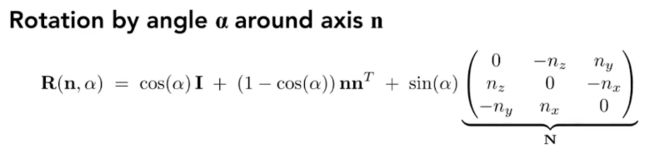
这里贴一张百度上的证明过程:
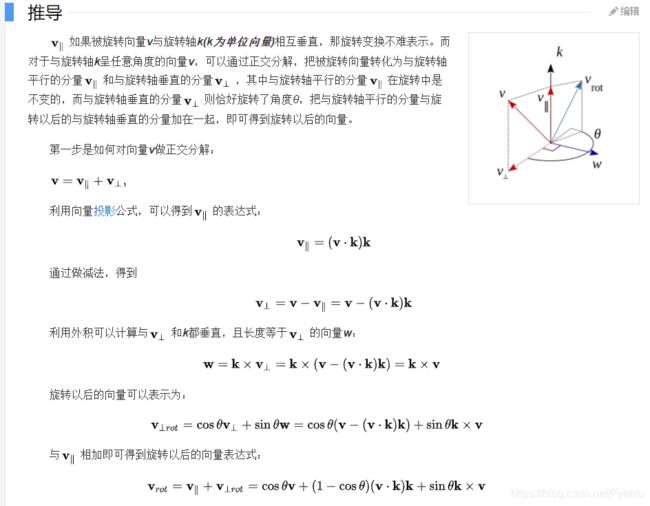
对于复杂的旋转问题,我们都可以将其拆解为简单旋转的叠加,也就是图形学中的Rodrigues旋转公式,其中传入的n为旋转轴上某点的坐标。 Rodrigues 公式定义了一个方向和一个旋转轴,方向可以理解,但轴我们默认为了是绕着过原点的轴旋转,这样才好拆分旋转,那么我们如果绕的轴不是过原点的轴呢?我们如果想让他沿着任意轴旋转怎么办,也就是轴可以平移怎么办,这就用到了我们之前学到的,我们可以先将轴的起点移到原点上,再进行旋转,再将点从原点移回原来的位置。关于该公式还有一点需要注意,就是后面有一个矩阵的形式N,我们之前提到了向量和向量是可以做叉积的,最后得到的结果是一个向量。所以我们可以将第一个向量写成矩阵的形式,那么矩阵乘以第二个向量得到的形式就是矩阵的形式,这也就是叉乘的结果,所以这里的N也就是某一个叉乘,我们想将其写成矩阵的形式。
//得到绕任意过原点的轴的旋转变换矩阵,根据传入的axis来进行旋转,axis是与原点形成轴的点坐标
Eigen::Matrix4f get_rotation_matrix(Vector3f axis, float angle)
{
Eigen::Matrix4f rotation = Eigen::Matrix4f::Identity();
Eigen::Matrix3f N, R; //R是罗德里格斯矩阵
Eigen::Matrix3f I = Eigen::Matrix3f::Identity(); //I是单位矩阵
double rotate = angle * 3.14 / 180.0f;
N << 0, -axis[2], axis[1],
axis[2], 0, -axis[1],
-axis[1], axis[0], 0;
R = std::cos(rotate) * I + (1 - std::cos(rotate)) * axis * axis.transpose() + std::sin(rotate) * N;
//向量的transpose()函数可以求该向量的转置
rotation << R(0, 0), R(0, 1), R(0, 2), 0,
R(1, 0), R(1, 1), R(1, 2), 0,
R(2, 0), R(2, 1), R(2, 2), 0,
0, 0, 0, 1;
return rotation;
}
补充:四元数
四元数概念的引入更多的是为了旋转与旋转之间的差值,就比如二维空间下(不考虑齐次坐标)旋转25°和15°,将这两个矩阵加起来求平均,得到的矩阵并不是旋转20°得到的矩阵,因此旋转矩阵在这方面是不适合做差值的,考虑到这点,所以引入了四元数。学习找到四元数,并且学习如何与旋转矩阵进行转化
二、视图变换(View transformation)
我们在准备视图变换的时候,需要定义三个量:
①“相机”所处的位置 e
②“相机”朝向的方向 g
③“相机”向上的方向,也就是相机本身的旋转,会导致成像是否为旋转的 t
定义以上三个方向的向量,我们就可以将相机本身如何成像给固定下来了。

定义了相机的朝向始终是对着-z方向,这样图像映射到屏幕上的方向就是+z方向,相机的向上方向始终是对着y方向,相机始终固定在原点。
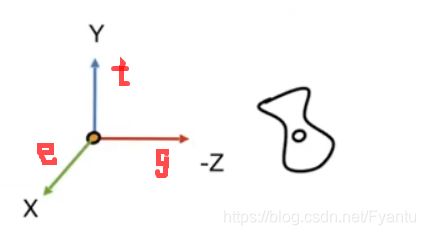
因此我们首先将“相机”位置移到原点,然后再利用线性变换将g对着-z方向,t对着y方向,这样e自然就对着x方向,**这里我们需要注意,写一个齐次矩阵是先做线性变换在做平移,而在这里是先做平移再做线性变换。**由于我们这里求原始的旋转不好求,但是我们旋转后的结果是互相正交的标准坐标系,是很好写的,因此我们可以很好的求出旋转矩阵的逆矩阵

例如,其中的逆矩阵乘以一个向量[1,0,0,0]就可以得到X对到g x t方向后x,y,z的坐标,由此类推其他,所以我们可以得到视图变换的矩阵:
![]()
因此将相机落到这个固定的位置上,其他物体也自然的落到了这个所需要的位置上
/*传入摄像机坐标(将摄像机移动到原点,同时移动其他所有物体,因为摄像机和物体都是运动同样位置,所以相对位置其实不变)*/
Eigen::Matrix4f get_view_matrix(Eigen::Vector3f eye_pos)
{
//初始化view为单位矩阵(用来返回)
Eigen::Matrix4f view = Eigen::Matrix4f::Identity();
Eigen::Matrix4f translate;
//移动到原点
translate << 1, 0, 0, -eye_pos[0], 0, 1, 0, -eye_pos[1], 0, 0, 1,
-eye_pos[2], 0, 0, 0, 1;
//单位矩阵乘以矩阵A还是等于A
view = translate * view;
return view;
}
三、投影变换(Projection transformation)
我们在绘制图的时候,会有两种方式绘制立方体,一种是正交投影,他里面立方体的棱是平行的,另外一种则是透视投影,他里面的棱则会相交,这两种视图最本质的区别是:正交投影不会产生近大远小的现象,而透视投影可以在图形学中,正交投影相当于让相机放的无限远,光都是平行射入相机,而在透视投影中则是光从远处汇集到相机那一点。
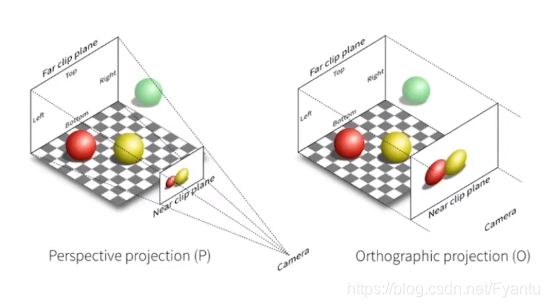
1.正交变换(Orthographic projection Transformation)
我们的正交投影在图形学中实际上就是包含两步:
①将一个任意形状的立方体的中心移到原点上来
②对各坐标轴进行缩放或扩大来将立方体映射为一个正方体。
我们定义了空间中这个立方体的左右,也即x轴上;下上,也即y轴上;前后,也即z轴上,其中注意,由于我们看的是-z方向,所以其实一个物体离我们近,那么z值比较大,离我们远,则z值比较小,所以在这里远是小于近的。这也是我们为了保证右手坐标系才这样设定的,所以有一些图形API为了保证远大于近,所以设了左手系,比如OpenGL,但这样会导致x叉乘y不再等于z,所以有的答案正好是负的,是因为坐标系不同导致的。

所以我们可以很容易的得到相应的转换矩阵,其中平移矩阵为负号是因为要向所处区域的负方向移动,变换矩阵分子为2则是因为分母的距离是整个棱长,而我们只需要棱长的一半进行放缩即可。
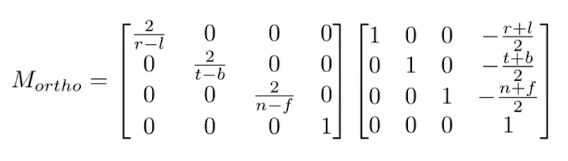
经过计算即可得:

2.投影变换(Perspective projection Transformation)
首先我们回顾当初学齐次坐标时,我们定义了点(x,y,z,1)与(kx,ky,kz,k)是同一个点(k≠0)
我们观察透视投影和正交投影的区别,无非是透视投影是从一个大的远景上投到一个小的近景(Frustum)上,而正交透影则是远景近景都很小。因此我们想到了一个办法,就是先将远景“挤”成近景,然后在对近景进行正交投影,就完成了透视投影。
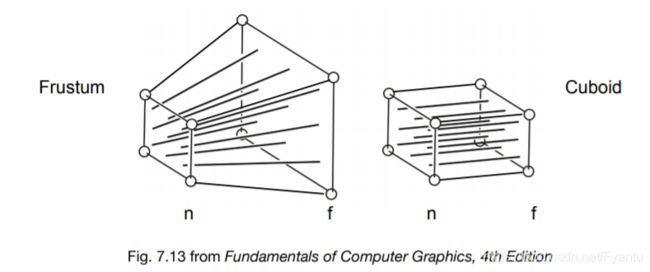
在“挤”的过程中,我们规定近平面永远不变,对远平面的“挤”则要保持z值永远不变,以及两平面的中心点也不会发生变化。“挤”的过程其实就是一个相似三角形的关系,其中x,y,z我们都知道,唯独n不知道:


所以我们可以得到齐次坐标这个公式,其中z变换后得到n我们是未知的
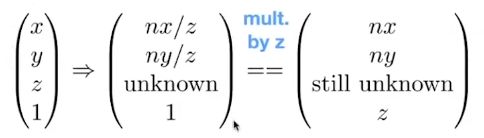
所以我们可以得到一个公式,即为一个代表“挤”操作的矩阵乘上(x,y,z,1)后得到对应向量:

所以我们可以推得这个矩阵的部分:
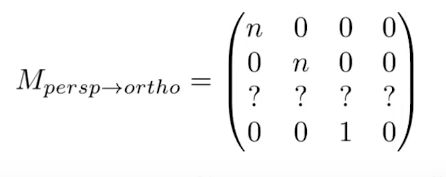
我们此时可以用到前面定义的两个概念,即近处的点完全不变,远处的点z不变,而该矩阵第三行代表的即为对z的变化,因此我们可以设立一个向量为(x,y,n,1),它近处的点通过映射还是变为它自己也就是(nx,ny,n²,n),由此我们得出公式:

这里面前面两项必为0是因为所得的结果由于不含x、y,所以一定为0,但后面两项不能确定,可以A=N,B=0,也可以A=0,B=n²。我们再利用远平面的(0,0,f,1)映射后还是(0,0,f,1),因此我们可以得到类似的式子:

将两个式子联立,可以得到:

即可得到我们的透视矩阵:

所以我们再把正交投影的矩阵与其相乘,即可得到透视投影的矩阵:

将前面的矩阵进行计算即可得:

接下来有一个小问题,那就是中间的点,在经过挤压以后,其z值是更偏向近处n还是远处f,我们可以假设中间向量为(0,0,(n+f)/2,1),那么将M透视与他相乘后,可以得到新的向量

因此我们可以看出来变换后的z是变近还是变远,取决于原来的n和f值
我们得到了通过透视投影可以得到一个画面,我们对这个画面定义了两个概念:分别是长宽比和透视角度(默认为垂直的,当然也可以通过垂直的来求水平的)
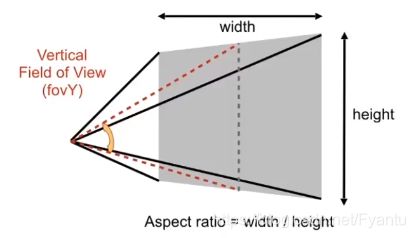
将这两个概念带入原来的定义,那么我们可以用之前的量的来表示这两个概念:
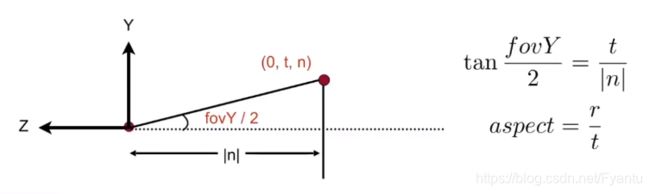
所以我们一旦定义了一个角度和宽高比就可以得到其他的远近,左右,上下的量。
//eye_fov 视场角
//aspect_ratio 纵横比(长宽比)
//zNear 视锥Frustum的近平面与摄影机的单位距离(视为不变)
//zFar 视锥Frustum的远平面与摄影机的单位距离(视为不变)
//透视矩阵=正交矩阵*透视矩阵->正交矩阵
//构建透视投影
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
// Students will implement this function
//初始化为单位矩阵
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
//正交矩阵
Eigen::Matrix4f orth = Eigen::Matrix4f::Identity();
//透视矩阵->正交矩阵
Eigen::Matrix4f pertoorth = Eigen::Matrix4f::Identity();
float halfEyeAngelRadian = eye_fov / 2 / 180.0 * MY_PI;
//传入的只是znear和zfar,不是坐标,因为是z轴负半轴所以是负的
float n = -1 * zNear;
float f = -1 * zFar;
//可以看一下图,应该一看就明白了
float t = zNear * std::tan(halfEyeAngelRadian);// top / znear = tan(halfEyeAngelRadian)
float r = t * aspect_ratio;// top / right = aspect_ration
float l = (-1) * r;//
float b = (-1) * t;//
orth << 2 / (r - l), 0, 0, 0,
0, 2 / (t - b), 0, 0,
0, 0, 2 / zNear - zFar, 0,
0, 0, 0, 1;
pertoorth << n, 0, 0, 0,
0, n, 0, 0,
0, 0,n + f, -1 * n * f,
0, 0, 1, 0;
projection = orth * pertoorth;
return projection;
}
四、视口变换(Viewport Transformation)
在图形学中,屏幕其实就是一个二维的数组,里面存的是像素,其中我们用分辨率来表示像素(Pixel)的多少,例如1980*720即为我们常见的720p,在图形学中,我们定义了像素为一个一个的小方块,每个像素有着一个颜色并且方块该颜色是均匀的,我们用三个数字来表示它红绿蓝(RGB)三色的强度等级,组合在一起的颜色即为该像素块的颜色。
屏幕是一个典型的光栅成像设备(光栅即为屏幕),光栅化即为把东西画在屏幕上。在图形学中,我们定义像素的坐标都在(0,0)与(width-1,height-1)中,屏幕的范围则在(0,0)到(width,height)中,但由于像素是一个一个边长为1的方块,所以像素的中心点坐标实际上为(x+0.5,y+0.5)

所以我们要在x,y方向上的[-1,1]的二维空间映射到[0,width]x[0,height]的空间上,我们要先对其进行放缩,然后再将原点从(0,0)移到(width/2,height/2)所以视口变换的矩阵为:

Reference
[1]百度百科——罗德里格旋转公式
[2]计算机图形学二:视图变换(坐标系转化,正交投影,透视投影,视口变换)
