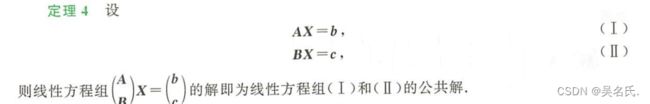线性代数基础【4】线性方程组

第四章 线性方程组

一、线性方程组的基本概念与表达形式

二、线性方程组解的基本定理

定理1 设A为mXn矩阵,则

(1)齐次线性方程组AX=0 只有零解的充分必要条件是r(A)=n;

(2)齐次线性方程组AX=0 有非零解(或有无数个解)的充分必要条件是r(A)＜n

推论1 设A为n阶矩阵,则

(1)齐次线性方程组AX=0只有零解的充分必要条件是|A|≠0;

(2)齐次线性方程组AX=0有非零解(或有无数个解)的充分必要条件是|A|=0

注意:

①齐次线性方程组系数矩阵的秩相当于方程组中约束条件的个数，当 r(A)=n 时，表示齐次线性方程组中未知数的个数与约束条件的个数相等,即没有自由变量,故齐次线性方程组只有零解;当 r(A)

定理2 设A为mxn矩阵,增广矩阵A增=(A:b),则

(1)非齐次线性方程组AX=b 有解的充分必要条件是r(A增)=r(A),其中当r(A增)=r(A)=n时,非齐次线性方程组AX=b有唯一解;当r(增A)=r(A)

(2)非齐次线性方程组AX=b 无解的充分必要条件是r(A增)≠r(A)

推论2 设A是n阶矩阵,则

(1)非齐次线性方程组AX=b 有解的充分必要条件是r(A增)=r(A)其中当|A|≠0时方程组有唯一解;当|A|=0 时,方程组有无数个解;

(2)非齐次线性方程组AX=b 无解的充分必要条件是r(A增)≠r(A)

注意:

三、线性方程组解的结构

1.设X1,X2,…,Xs为齐次线性方程组AX=0的一组解,则k1X1,+k2X2+…+ksxs也为齐次线性方程组AX=0的解,其中k1,k2,…,ks，为任意常数

2.设η0为非齐次线性方程组AX=b 的一个解,X1,X2,…,Xn为齐次线性方程组AX=0的一组解,则k1X1+k2X2+…+ksxs+η0为非齐次线性方程组 AX=b 的解

3.设η1,η2为非齐次线性方组AX=b 的两个解，则η2-η1为齐次性方组AX=0的一个解.

4.设X1,X2,…,Xs,为非齐次线性方程组AX=b的一组解,则k1X1+k2X2+…+ksXs为AX=b的解的充分必要条件是k1+k2+…+ks=1.

5.设η1,η2,…,ηs,为非齐次线性方程组AX=b 的一组解,则 k1η1+k2η2+···+ksηs,为齐次线性方程组AX=0 的解的充分必要条件是 k1+k2+…+ks=0.

四、线性方程组的组解

1.齐次线性方程组 AX=0 的基础解系与通解

(1)基础解系——设r(A)=r

求齐次线性方程组的基础解系时,把其系数矩阵通过初等行变换进行阶梯化(系数矩阵进行初等行变换相当于方程组的同解变形),每行第一个非零元素所在的列对应的未知数是约束变量,其余变量为自由变量,从而可以确定基础解系(最好把每行第一个非零元素化为1(归一性),且其所在的列其余元素都化为零(排他性))

如:对齐次线性方程组AX=0的系数矩阵A 进行初等行变换，化为

则r(A)=3<5,方程组AX=0的基础解系含有n-r=5-3=2个线性无关的解向量,其中x1,x2,x3为约束变量,x4,x5为自由变量,(x4,x5)分别取(1,0)和(0,1),则基础解系为

ξ1=(-2,1,一3,1,0)^T ξ2=(3,-4,2,0,1)^T

又如:对齐次线性方程组AX=0的系数矩阵A进行初等行变换，化为

则r(A)=2<5,方程组AX=0的基础解系含有n-r=5-2=3 个线性无关的解向量,其中x1,x3为约束变量,x2,x4,x5为自由变量,(x2,x4,x5)分别取(1,0,0),(0,1,0)及(0,0,1),则基础解系为

ξ1=(1,1;0,0,0)^T ξ2=(-2,0,-1,1,0)^T ξ3=(-4,0,2,0,1)^T

注意:

设A为mXn 矩阵且r(A)=r

(1)该向量组中每个向量都是AX=0的解;

(2)该向量组线性无关:

(3)该向量组所含解向量的个数等于n-r

(2)通解——设ξ1,ξ2,…,ξn-r为齐次线性方程组AX=0的一个基础解系,则称k1ξ1+k2ξ12+…+k(n-r)ξ(n-r)，为齐次线性方程组AX=0的通解,其中k1,k2,…,k(n-r)为任意常数.

2.非齐次线性方程组AX=b的通解

设r(A)=r(A增)=r

k1ξ1+k2ξ2+…+k(n-r)ξ(n-r)+η0，其中k1,k2,…,k(n-r)，为任意常数

注意:

五、线性方程组的理论延伸

定理1 设A是mXn矩阵,B是nXs矩阵,若AB=0则B的列向量组为方程组AX=0的解

定理2 设方程组AX=0与BX=0为同解方程组，则r(A)=r(B),反之不对

定理3 设方程组AX=0的解为BX=0的解,则r(A)≥r(B)

注意:

1.若方程组AX=0的解为方程组BX=0的解，方程组BX=0的解不全是方程组AX=0的解，则r(A)>r(B)

2.若方程组AX=0的解为方程组 BX=0的解，且r(A)=r(B),则方程组AX=0与方程组BX=0同解

定理4