Leetcoder Day1|数组理论|二分查找|移除元素
目录
数组理论基础
704.二分查找
解题思路:
35.搜索插入位置
27. 移除元素
解题思路:
暴力解法
双指针方法
今日心得
数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合
- 下标都是从0开始的
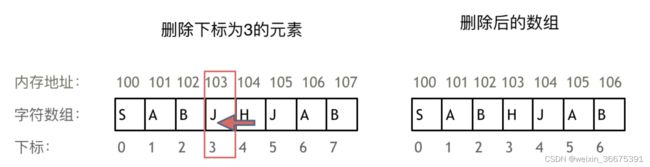
- 内存空间的地址是连续的——>增删需移动其他元素的地址
- 数组元素不能被删除,只能覆盖
C++中,vector的底层实现是array,是容器,不是数组,且C++中二维数组在地址空间上是连续的。
704.二分查找
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。
- 你可以假设
nums中的所有元素是不重复的。n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
适用条件:数组有序无重复元素
解题思路:
- <还是<=
- 要不要+1/-1
实际就是判断在区间中是否合法,要注意区间是左闭右闭还是左闭右开:
左闭右闭:r=numsize-1,while l <= r(因为left == right是有意义的,所以使用 <=),每个mid做大于、小于、等于三次判断,更新边界时因为已经确定mid不等于target,要更新为l=mid+1或r=mid-1,在等于时结束循环输出mid,即所求下标;循环结束未输出说明不在区间里。
class Solution {
public:
int search(vector& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
左闭右开:r=numsize,while l < r(因为left == right在区间[left, right)是没有意义的),每个mid做大于、小于、等于三次判断,因为更新边界时,r不在区间内,因此可以更新为r=mid,但更新l需要在区间内,因此仍然l=mid+1。
class Solution {
public:
int search(vector& nums, int target) {
int left = 0;
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
}; - 时间复杂度:O(log n)
- 空间复杂度:O(1)
Java实现情况:0 ms 44.6 MB
C++实现情况:20 ms 27.3 MB
35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
本题首先需要考虑下面可能的情况:
目标值等于数组中某一个元素:思路跟704类似
目标值不存在于数组中:
- 目标值在数组所有元素之前
- 目标值插入数组中的位置
- 目标值在数组所有元素之后
暴力解法对于本题复杂度并是很高,因为只用了一层for循环进行遍历,找到相等的返回,不存在的插入即可。
class Solution {
public:
int searchInsert(vector& nums, int target) {
for (int i = 0; i < nums.size(); i++) {
// 分别处理如下三种情况
// 目标值在数组所有元素之前
// 目标值等于数组中某一个元素
// 目标值插入数组中的位置
if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i],那么i就是我们要的结果
return i;
}
}
// 目标值在数组所有元素之后的情况
return nums.size(); // 如果target是最大的,或者 nums为空,则返回nums的长度
}
}; 二分查找法在目标值存在于数组中的情况时,与704思路基本一致。如果目标值不存在于数组中,假如在数组所有元素之前,由于左闭右开的情况下,当找不到目标值时,意味着遇到了left>right的情况,那么left就是需要插入的位置,因此返回left的值即可(这里随想录里给的是right+1,我一开始没有想明白,所以写了left更能说得通一些。)
class Solution {
public:
int searchInsert(vector& nums, int target) {
int left=0;
int right=nums.size()-1;
while(left<=right){
int mid=(right-left)/2+left;
if(nums[mid]>target){ //左闭右闭
right=mid-1;
}
else if(nums[mid] 27. 移除元素
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 104nums已按 非严格递增 排列
适用条件:原地操作,链表求环、链表求中点、数组中元素替换与查找等
erase是一个时间复杂度为O(n)的操作,本质是i--
解题思路:
暴力解法
通过两层for循环将数组内为 val 的元素覆盖,每遇到一个和val相等的元素,便将后面的元素前移覆盖,但是时间复杂度过高为O(N^2)。
class Solution {
public int removeElement(int[] nums, int val) {
int size=nums.length;
for(int i=0; i用暴力解法时,将后面的所有元素前移后,要进行i--操作,将i还原回去判断覆盖后的新元素是否也等于val,第一次尝试的时候没有进行i--操作,而且还出现了将size--放错括号的情况。
双指针方法
设置快慢两个指针,快指针按顺序遍历数组,遇到不等于val的值,便将其值赋值给慢指针,然后让慢指针前进,遇到等于val的值,便让慢指针原地等待,起到删除作用。⚠️要先赋值再让慢指针前进。时间复杂度: O ( N )。
class Solution {
public:
int removeElement(vector& nums, int val) {
int slow = 0;
for (int fast = 0; fast < nums.size(); fast++) {
if (val != nums[fast]) {
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
}; 除了快慢指针,还有双向指针也即左右指针,和二分类中左闭右闭情况类似,设置左右指针,让左指针从左向右遍历,若左指针指向的元素值不等于val,左指针向后移;当遇到等于val的元素时,将右指针指向的元素值赋给左指针当前所指的位置,右指针向前移动,意味着数组长度-1;这个方法减少了元素移动的次数但是改变了数组的顺序。
今日心得
今天的两道题目思路都有,毕竟考研的时候也有复习过,但是语法不熟练而且在很多实现细节上面会有遗漏。最大的收获是明确了很多细节上的要点,并且用更加理解而非死记硬背的方法梳理了思路。每道题和思路基本都用C++和java各实现了一遍,算是顺便复习了语法。总用时2小时,写博客和总结花费较多时间,继续努力。