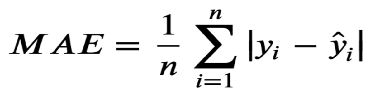快速了解——交叉验证和网格搜索 以及损失函数

一、交叉验证 和 网格搜索

目的：调整超参数

        对于KNN来说，可以调整的参数包括

                K：邻居的个数

                P：距离度量方式

1、交叉验证

        概述：训练数据 划分为 训练集、验证集

        stratify：分层划分，stratify = y 保证训练集、测试集一致

        （当数据中一个类别数量很多，一个很小，要设置这个参数）

2、网格搜索

        概述：遍历所有参数组合，训练模型，找最佳参数组合

        每一个参数组合，都会计算cv次，每次的评估指标计算平均值，通过指标平均值来判断哪组参数最好

3、API

        1. 导包

        from sklearn.model_selection import GridSearchCV

        GridSearchCV：交叉验证

        2. 创建K近邻模型对象        

        knn_estimator = KNeighborsClassifier(n_neighbors = 3)

        n_neighbors：KNN中k的取值

        param_grid_ = { ' n_neighbors ' ：[ 2，3，4，5，6 ]，' p ' ：[1，2]，' weights ' ：[ ' uniform '，' distance ' ] }

        p：1曼哈顿距离，2欧氏距离

        weights：投票时的权重

                uniform：平权投票（默认），所有的样本权重都一样

                distance：加权投票，考虑距离的倒数作为权重

        grid_estimator = GridSearchCV(estimator = knn_estimator，param_grid = param_grid_，cv = 4)
        cv = 4：把训练集划分成4份，3份用来训练，1份用来验证

        3. 训练模型

        grid_estimator.fit(x_train_scaled，y_train)

        4. 预测分类

        y_train_pred=grid_estimator.predict(x_train_scaled)

        y_test_pred=grid_estimator.predict(x_test_scaled)

        5. 模型评估

        交叉验证网格搜索的全部过程，每组验证集的评价结果：        

                grid_estimator.cv_results_

        最佳分数：grid_estimator.best_score_

        最佳的参数组合：grid_estimator.best_params_

        最佳的分类器：grid_estimator.best_estimator_

二、线性回归

        概述：利用 回归方程 对 特征值 和目标值的关系建模的分析方法

        导包：from sklearn.linear_model import LinearRegression

        创建线性回归对象：estimator = LinearRegression( )

        求解的基本思路：构造 假设函数：y = kx + b

                                     确定 损失函数

1、 损失函数

        概述：也称为代价、成本、目标函数，衡量每个样本 预测值 与 真实值 效果的函数

        种类：

                1. 均方误差（MSE）：Mean Square Error，越小，模型预测越准确

                                                 n 为样本数量，y 为实际值，y ̂ 为预测值

                                导包：from sklearn.metrics import mean_squared_error

                                调用：mean_squared_error(y_test，y_predict)

                2. 平均绝对误差（MAE）：Mean Absolute Error 对误差大小不敏感

                                 导包：from sklearn.metrics import mean_absolute_error

                                调用：mean_absolute_error(y_test，y_predict)

                3. 均方根误差（RMSE）：Root Mean Squared Error 对异常点更加敏感，RMSE 是

MSE 的平方根，某些情况下比MSE更有用

         tips：如果RMSE指标训练的非常低，说明模型对异常点（对噪声）也拟合的非常好，容易 过拟合

2、优化方法

        1. 梯度下降法

        梯度：（矢量）梯度的方向就是上升最快的方向；单变量函数，梯度为 某一点切线斜率，有

                     方向为函数增长最快的方向；多变量函数，梯度为 某一点的 偏导数，有方向，偏导

                     数分量的向量方向

        步长（学习率）：在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度；

                                     太小，下降速度会慢；太大，容易错过最低点、产生下降过程中的震荡、

                                     甚至梯度爆炸

        公式：w = w - a * 梯度

                                                 a：步长        w：权重

        过程：     1、给定初始位置 W、步长（学习率）

                        2、计算该点 当前的梯度的负方向

                        3、向负方向移动步长，更新W

                        4、重复2、3 直至收敛（两次差距小于指定的阈值，或者达到指定的迭代次数）

        API：from sklearn.linear_model import SGDRegressor ( loss = "squared_loss"，

                 fit_intercept = True，learning_rate = 'constant'，eta0 = 0.01)

                loss：损失函数类型

                learning_rate：学习率策略

                eta0：学习率的值

                学习率不断变小策略： ‘ invscaling ’ ：eta = eta0 / pow(t, power_t = 0.25)

        分类：

        全 梯度下降算法 FGD：更新权重时，使用全部样本，训练速度较慢

        随机 梯度下降算法 SGD：每轮随机挑一个样本，简单、高效、不稳定，遇到噪声容易陷入局

                                                  部最优解

        小批量 梯度下降算法 mini-bantch：每轮随机挑一小批样本，结合了 SG 和 FG，最常用

        随机平均 梯度下降算法 SAG：每轮随机挑一个样本并记录，下一轮再挑一个，并计算两个梯

                                                         度的平均值，初期表现不佳

        2. 求方程法（求导、求偏导）

        正规方程：只对 线性回归 有用，不是所有的矩阵都有逆矩阵

        公式：

         API：from sklearn.linear_model import LinearRegression ( fit_intercept = True )

                  fit_intercept：是否计算偏置

                  estimator = LinearRegression( )

                  查看属性：

                                模型的权重系数，回归系数（斜率）：estimator.coef_

                                偏置，截距：estimator.intercept_