【机器学习】聚类算法(二)
五、基于密度的算法
5.1 DBSCAN 算法
import sys # 导入 sys 模块,用于访问系统相关的参数和功能
import os # 导入 os 模块,用于处理文件和目录
import math # 导入 math 模块,用于进行数学运算
import random # 导入 random 模块,用于生成随机数
from sklearn import datasets # 导入 sklearn 的 datasets 模块,用于加载数据集
import numpy as np # 导入 numpy 模块,用于进行科学计算,简写为 np
# Import helper functions
dir_path = os.path.dirname(os.path.realpath(__file__)) # 获取当前文件的绝对路径
sys.path.insert(0, dir_path + "/../utils") # 将 utils 目录添加到系统路径中,方便导入其中的模块
from utils.data_manipulation import normalize # 从 utils.data_manipulation 模块中导入 normalize 函数,用于对数据进行归一化处理
from utils.data_operation import euclidean_distance # 从 utils.data_operation 模块中导入 euclidean_distance 函数,用于计算欧几里得距离
sys.path.insert(0, dir_path + "/../unsupervised_learning/") # 将 unsupervised_learning 目录添加到系统路径中,方便导入其中的模块
from principal_component_analysis import PCA # 从 principal_component_analysis 模块中导入 PCA 类,用于进行主成分分析
# 定义 DBSCAN 类,用于实现 DBSCAN 算法
class DBSCAN():
# 初始化方法,接受两个参数:eps 和 min_samples
def __init__(self, eps=1, min_samples=5):
self.eps = eps # eps 表示邻域半径,用于判断两个样本是否为邻居
self.min_samples = min_samples # min_samples 表示核心点的最小邻居数,用于判断一个样本是否为核心点
# List of arrays (clusters) containing sample indices
self.clusters = [] # clusters 表示聚类结果,是一个列表,每个元素是一个数组,表示一个簇,包含了样本的索引
self.visited_samples = [] # visited_samples 表示已经访问过的样本的索引,是一个列表
# Hashmap {"sample_index": [neighbor1, neighbor2, ...]}
self.neighbors = {} # neighbors 表示每个样本的邻居,是一个字典,键是样本的索引,值是一个数组,表示该样本的邻居的索引
self.X = None # Dataset # X 表示数据集,是一个二维数组,每一行是一个样本,每一列是一个特征
# 定义一个私有方法,用于获取一个样本的邻居,接受一个参数:sample_i,表示样本的索引
def _get_neighbors(self, sample_i):
neighbors = [] # 定义一个空列表,用于存储邻居的索引
for _sample_i, _sample in enumerate(self.X): # 遍历数据集中的每个样本及其索引
if _sample_i != sample_i and euclidean_distance( # 如果样本的索引不等于 sample_i,且样本与 sample_i 对应的样本的欧几里得距离小于 eps
self.X[sample_i], _sample) < self.eps:
neighbors.append(_sample_i) # 则将该样本的索引添加到邻居列表中
return np.array(neighbors) # 返回邻居列表,转换为 numpy 数组
# 定义一个私有方法,用于扩展一个簇,接受两个参数:sample_i 和 neighbors,分别表示样本的索引和邻居
def _expand_cluster(self, sample_i, neighbors):
cluster = [sample_i] # 定义一个列表,用于存储簇中的样本的索引,初始值为 sample_i
# Iterate through neighbors
for neighbor_i in neighbors: # 遍历邻居中的每个样本的索引
if not neighbor_i in self.visited_samples: # 如果该样本的索引不在已访问过的样本列表中
self.visited_samples.append(neighbor_i) # 则将该样本的索引添加到已访问过的样本列表中
# Fetch the samples distant neighbors
self.neighbors[neighbor_i] = self._get_neighbors(neighbor_i) # 获取该样本的邻居,并存储到 neighbors 字典中
# Make sure the neighbors neighbors are more than min_samples
if len(self.neighbors[neighbor_i]) >= self.min_samples: # 如果该样本的邻居数大于等于 min_samples,即该样本是一个核心点
# Choose neighbors of neighbor except for sample
distant_neighbors = self.neighbors[neighbor_i][ # 选择该样本的邻居中除了 sample_i 之外的样本,作为远邻
np.where(self.neighbors[neighbor_i] != sample_i)]
# Add the neighbors neighbors as neighbors of sample
self.neighbors[sample_i] = np.concatenate( # 将远邻添加到 sample_i 的邻居中
(self.neighbors[sample_i], distant_neighbors))
# Expand the cluster from the neighbor
expanded_cluster = self._expand_cluster( # 从该样本开始递归地扩展簇
neighbor_i, self.neighbors[neighbor_i])
# Add expanded cluster to this cluster
cluster = cluster + expanded_cluster # 将扩展后的簇添加到当前簇中
if not neighbor_i in np.array(self.clusters): # 如果该样本的索引不在已经形成的簇中
cluster.append(neighbor_i) # 则将该样本的索引添加到当前簇中
return cluster # 返回当前簇
# 定义一个私有方法,用于获取簇的标签,即每个样本所属的簇的编号
def _get_cluster_labels(self):
# Set default value to number of clusters
# Will make sure all outliers have same cluster label
labels = len(self.clusters) * np.ones(np.shape(self.X)[0]) # 定义一个数组,用于存储簇的标签,初始值为簇的个数,这样可以保证所有的离群点都有相同的标签
for cluster_i, cluster in enumerate(self.clusters): # 遍历每个簇及其编号
for sample_i in cluster: # 遍历簇中的每个样本的索引
labels[sample_i] = cluster_i # 将样本的标签设置为簇的编号
return labels # 返回簇的标签
# 定义一个公开方法,用于对数据集进行聚类,接受一个参数:X,表示数据集
def predict(self, X):
self.X = X # 将数据集赋值给 self.X
n_samples = np.shape(self.X)[0] # 获取数据集的样本数
for sample_i in range(n_samples): # 遍历每个样本的索引
if sample_i in self.visited_samples: # 如果该样本已经访问过
continue # 则跳过该样本
self.neighbors[sample_i] = self._get_neighbors(sample_i) # 获取该样本的邻居,并存储到 neighbors 字典中
if len(self.neighbors[sample_i]) >= self.min_samples: # 如果该样本的邻居数大于等于 min_samples,即该样本是一个核心点
self.visited_samples.append(sample_i) # 则将该样本的索引添加到已访问过的样本列表中
new_cluster = self._expand_cluster( # 从该样本开始扩展一个新的簇
sample_i, self.neighbors[sample_i])
self.clusters.append(new_cluster) # 将新的簇添加到聚类结果中
cluster_labels = self._get_cluster_labels() # 获取簇的标签
return cluster_labels
def main(): # 定义一个主函数,用于执行聚类任务
# Load the dataset
X, y = datasets.make_moons(n_samples=300, noise=0.1) # 加载数据集,使用 sklearn 的 datasets 模块中的 make_moons 函数生成两个月牙形状的数据,X 是特征矩阵,y 是真实的类别标签
# Cluster the data using DBSCAN
clf = DBSCAN(eps=0.17, min_samples=5) # 创建一个 DBSCAN 类的实例,指定 eps 和 min_samples 参数
y_pred = clf.predict(X) # 调用 predict 方法对数据集 X 进行聚类,返回聚类后的类别标签
# Project the data onto the 2 primary principal components
pca = PCA() # 创建一个 PCA 类的实例,用于进行主成分分析
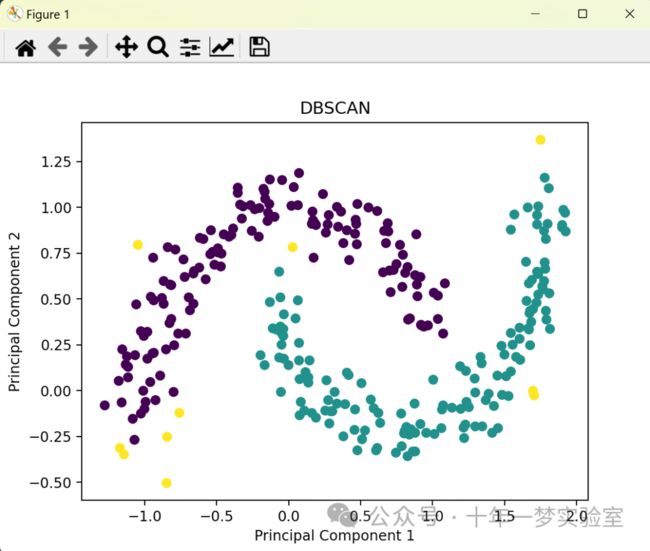
pca.plot_in_2d(X, y_pred, title="DBSCAN") # 调用 plot_in_2d 方法将数据集 X 投影到两个主成分上,并根据聚类后的类别标签 y_pred 绘制散点图,标题为 "DBSCAN"
pca.plot_in_2d(X, y, title="Actual Clustering") # 调用 plot_in_2d 方法将数据集 X 投影到两个主成分上,并根据真实的类别标签 y 绘制散点图,标题为 "Actual Clustering"
if __name__ == "__main__": # 如果当前文件是主程序
main() # 则调用主函数输出:
5.2 OPTICS算法
OPTICS 聚类算法演示
这段代码的目的是使用 OPTICS 算法对六个簇的数据进行聚类分析,并与不同的 epsilon 值的 DBSCAN 聚类进行比较。代码的主要步骤如下:
导入所需的模块,包括 matplotlib 用于绘图,numpy 用于数值计算,sklearn 用于机器学习
生成样本数据,每个簇的数据服从不同的正态分布,共有 1500 个点
创建一个 OPTICS 聚类器对象,设置相关的参数,如最小样本数,聚类稳定性参数,最小簇大小等
对样本数据进行拟合,得到 OPTICS 聚类的结果,包括每个点的可达性距离,核心距离,排序和簇标签
使用 cluster_optics_dbscan 函数,根据 OPTICS 聚类的输出,按照不同的 epsilon 值进行 DBSCAN 聚类,得到两组不同的簇标签
绘制四个子图,分别显示可达性图,OPTICS 聚类结果,epsilon 为 0.5 和 2 时的 DBSCAN 聚类结果
调整子图的布局,避免重叠,并显示图形
这段代码可以展示 OPTICS 聚类的优势,即不需要指定簇的个数,也不需要指定 epsilon 参数,而是可以根据数据的密度分布自动地进行聚类。同时,也可以展示不同的 epsilon 值对 DBSCAN 聚类的影响,即 epsilon 值越大,簇的个数越少,噪声点越多。
# 导入 matplotlib 的 gridspec 模块,用于绘制子图
import matplotlib.gridspec as gridspec
# 导入 matplotlib 的 pyplot 模块,用于绘制图形
import matplotlib.pyplot as plt
# 导入 numpy 模块,用于进行数值计算
import numpy as np
# 从 sklearn.cluster 模块导入 OPTICS 和 cluster_optics_dbscan 函数
from sklearn.cluster import OPTICS, cluster_optics_dbscan
# 生成样本数据
# 设置随机数种子,保证每次运行结果一致
np.random.seed(0)
# 设置每个簇的点数为 250
n_points_per_cluster = 250
# 生成六个簇的数据,每个簇的数据服从正态分布,不同簇的均值和方差不同
C1 = [-5, -2] + 0.8 * np.random.randn(n_points_per_cluster, 2)
C2 = [4, -1] + 0.1 * np.random.randn(n_points_per_cluster, 2)
C3 = [1, -2] + 0.2 * np.random.randn(n_points_per_cluster, 2)
C4 = [-2, 3] + 0.3 * np.random.randn(n_points_per_cluster, 2)
C5 = [3, -2] + 1.6 * np.random.randn(n_points_per_cluster, 2)
C6 = [5, 6] + 2 * np.random.randn(n_points_per_cluster, 2)
# 将六个簇的数据合并成一个数组
X = np.vstack((C1, C2, C3, C4, C5, C6))
# 创建一个 OPTICS 聚类器对象,设置最小样本数为 50,聚类稳定性参数为 0.05,最小簇大小为 0.05
clust = OPTICS(min_samples=50, xi=0.05, min_cluster_size=0.05)
# 对数据进行拟合,得到聚类结果
clust.fit(X)
# 使用 cluster_optics_dbscan 函数,根据 OPTICS 聚类器的输出,按照不同的 epsilon 值进行 DBSCAN 聚类
# epsilon 是 DBSCAN 聚类的一个参数,表示两个点之间的最大距离,小于等于 epsilon 的点被认为是相邻的
# 当 epsilon 为 0.5 时,得到 labels_050 数组,表示每个点的簇标签
labels_050 = cluster_optics_dbscan(
reachability=clust.reachability_,
core_distances=clust.core_distances_,
ordering=clust.ordering_,
eps=0.5,
)
# 当 epsilon 为 2 时,得到 labels_200 数组,表示每个点的簇标签
labels_200 = cluster_optics_dbscan(
reachability=clust.reachability_,
core_distances=clust.core_distances_,
ordering=clust.ordering_,
eps=2,
)
# 创建一个空间数组,表示每个点的序号
space = np.arange(len(X))
# 创建一个可达性数组,表示每个点的可达性距离,可达性距离是 OPTICS 聚类的一个概念,表示一个点到其最近的核心点的距离
# 核心点是指在其 epsilon 邻域内有足够多的点的点
# 可达性数组按照 OPTICS 聚类器的排序进行排列
reachability = clust.reachability_[clust.ordering_]
# 创建一个标签数组,表示每个点的簇标签,按照 OPTICS 聚类器的排序进行排列
labels = clust.labels_[clust.ordering_]
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 创建一个图形对象,设置大小为 10 x 7
plt.figure(figsize=(10, 7))
# 创建一个网格对象,用于放置子图,设置网格为 2 x 3
G = gridspec.GridSpec(2, 3)
# 创建四个子图对象,分别放在网格的不同位置
ax1 = plt.subplot(G[0, :])
ax2 = plt.subplot(G[1, 0])
ax3 = plt.subplot(G[1, 1])
ax4 = plt.subplot(G[1, 2])
# 绘制可达性图,可达性图是一种显示 OPTICS 聚类结果的图形,横轴是点的序号,纵轴是点的可达性距离
# 不同的颜色表示不同的簇,黑色的点表示噪声点,即没有被分配到任何簇的点
# 可达性图可以帮助选择合适的 epsilon 值进行 DBSCAN 聚类
colors = ["g.", "r.", "b.", "y.", "c."]
# 对于每个簇,用相应的颜色绘制其点的序号和可达性距离
for klass, color in zip(range(0, 5), colors):
Xk = space[labels == klass]
Rk = reachability[labels == klass]
ax1.plot(Xk, Rk, color, alpha=0.3)
# 对于噪声点,用黑色绘制其点的序号和可达性距离
ax1.plot(space[labels == -1], reachability[labels == -1], "k.", alpha=0.3)
# 用黑色实线绘制 epsilon 为 2 的水平线,表示 DBSCAN 聚类的一个划分点
ax1.plot(space, np.full_like(space, 2.0, dtype=float), "k-", alpha=0.5)
# 用黑色虚线绘制 epsilon 为 0.5 的水平线,表示 DBSCAN 聚类的另一个划分点
ax1.plot(space, np.full_like(space, 0.5, dtype=float), "k-.", alpha=0.5)
# 设置纵轴的标签为“可达性(epsilon 距离)”
ax1.set_ylabel("可达性(epsilon 距离)")
# 设置标题为“可达性图”
ax1.set_title("可达性图")
# 绘制 OPTICS 聚类的结果,横轴是数据的第一个特征,纵轴是数据的第二个特征
# 不同的颜色表示不同的簇,黑色的加号表示噪声点
colors = ["g.", "r.", "b.", "y.", "c."]
# 对于每个簇,用相应的颜色绘制其点的特征值
for klass, color in zip(range(0, 5), colors):
Xk = X[clust.labels_ == klass]
ax2.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)
# 对于噪声点,用黑色加号绘制其点的特征值
ax2.plot(X[clust.labels_ == -1, 0], X[clust.labels_ == -1, 1], "k+", alpha=0.1)
# 设置标题为“自动聚类\nOPTICS”
ax2.set_title("自动聚类\nOPTICS")
# 绘制 epsilon 为 0.5 时的 DBSCAN 聚类结果,横轴是数据的第一个特征,纵轴是数据的第二个特征
# 不同的颜色表示不同的簇,黑色的加号表示噪声点
colors = ["g.", "r.", "b.", "c."]
# 对于每个簇,用相应的颜色绘制其点的特征值
for klass, color in zip(range(0, 4), colors):
Xk = X[labels_050 == klass]
ax3.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)
# 对于噪声点,用黑色加号绘制其点的特征值
ax3.plot(X[labels_050 == -1, 0], X[labels_050 == -1, 1], "k+", alpha=0.1)
# 设置标题为“在 0.5 epsilon 切割处的聚类\nDBSCAN”
ax3.set_title("在 0.5 epsilon 切割处的聚类\nDBSCAN")
# 绘制 epsilon 为 2 时的 DBSCAN 聚类结果,横轴是数据的第一个特征,纵轴是数据的第二个特征
# 不同的颜色表示不同的簇,黑色的加号表示噪声点
colors = ["g.", "m.", "y.", "c."]
# 对于每个簇,用相应的颜色绘制其点的特征值
for klass, color in zip(range(0, 4), colors):
Xk = X[labels_200 == klass]
ax4.plot(Xk[:, 0], Xk[:, 1], color, alpha=0.3)
# 对于噪声点,用黑色加号绘制其点的特征值
ax4.plot(X[labels_200 == -1, 0], X[labels_200 == -1, 1], "k+", alpha=0.1)
# 设置标题为“在 2.0 epsilon 切割处的聚类\nDBSCAN”
ax4.set_title("在 2.0 epsilon 切割处的聚类\nDBSCAN")
# 调整子图的布局,避免重叠
plt.tight_layout()
# 显示图形
plt.show()输出:(噪声-灰色)
可达性图:显示了每个点的可达性距离,即一个点到其最近的核心点的距离。可达性图可以帮助选择合适的 epsilon 值进行 DBSCAN 聚类,不同颜色的区域表示不同的簇。
OPTICS 聚类:显示了 OPTICS 算法自动识别的簇,不需要指定簇的个数或 epsilon 值。不同颜色的点表示不同的簇,黑色的加号表示噪声点,即没有被分配到任何簇的点。
DBSCAN 聚类:显示了在不同的 epsilon 值下,使用 DBSCAN 算法的聚类结果,与 OPTICS 聚类进行比较。可以看出,epsilon 值的变化会影响 DBSCAN 聚类的效果,epsilon 值越大,簇的个数越少,噪声点越少。OPTICS 聚类则可以更好地适应不同密度的簇。
5.3 Mean Shift 算法
示例(scikit-learn)
# 导入 numpy 模块,用于进行数值计算
import numpy as np
# 从 sklearn.cluster 模块导入 MeanShift 函数,用于进行 Mean-Shift 聚类
from sklearn.cluster import MeanShift
# 从 sklearn.datasets 模块导入 make_blobs 函数,用于生成样本数据
from sklearn.datasets import make_blobs
# 导入 matplotlib.pyplot 模块,用于绘制图形
import matplotlib.pyplot as plt
# 使用 make_blobs 函数生成 300 个样本,分为 3 个簇,设置随机数种子为 42
# veri 是一个二维数组,表示样本的特征值,_ 是一个一维数组,表示样本的真实标签,这里不需要用到
veri, _ = make_blobs(n_samples=300, centers=3, random_state=42)
# 创建一个 Mean-Shift 聚类器对象,设置带宽参数为 2,带宽参数决定了邻域的大小
mean_shift = MeanShift(bandwidth=2)
# 对样本数据进行拟合,得到 Mean-Shift 聚类的结果
mean_shift.fit(veri)
# 获取聚类的中心点,是一个二维数组,每一行表示一个中心点的坐标
kume_merkezleri = mean_shift.cluster_centers_
# 获取聚类的标签,是一个一维数组,表示每个样本所属的簇的编号
etiketler = mean_shift.labels_
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# 创建一个图形对象,设置大小为 8 x 6
plt.figure(figsize=(8, 6))
# 绘制样本点的散点图,横轴是数据的第一个特征,纵轴是数据的第二个特征,颜色由聚类标签决定,使用 viridis 色彩映射,点的大小为 50,透明度为 0.7
plt.scatter(veri[:, 0], veri[:, 1], c=etiketler, cmap='viridis', s=50, alpha=0.7)
# 绘制聚类中心点的散点图,横轴是中心点的第一个坐标,纵轴是中心点的第二个坐标,颜色为红色,标记为 X,点的大小为 200,设置图例为“簇中心”
plt.scatter(kume_merkezleri[:, 0], kume_merkezleri[:, 1], color='red', marker='X', s=200, label='簇中心')
# 设置横轴的标签为“特征 1”
plt.xlabel('特征 1')
# 设置纵轴的标签为“特征 2”
plt.ylabel('特征 2')
# 设置标题为“Mean-Shift 聚类”
plt.title('Mean-Shift 聚类')
# 显示图例
plt.legend()
# 显示图形
plt.show()输出结果:
参考网址:
https://scikit-learn.org/stable/auto_examples/cluster/plot_optics.html#sphx-glr-auto-examples-cluster-plot-optics-py
https://scikit-learn.org/stable/modules/clustering.html#
附-scikit-learn OPTICS参数说明:
OPTICS(Ordering Points To Identify the Clustering Structure)算法说明
OPTICS(Ordering Points To Identify the Clustering Structure)是一种从向量数组中估算聚类结构的算法,与DBSCAN密切相关,它找到高密度的核心样本并从它们扩展聚类[1]。与DBSCAN不同的是,OPTICS保留了可变邻域半径的聚类层次结构。相对于当前scikit-learn实现的DBSCAN,OPTICS更适用于大型数据集。
聚类结果可以使用类似DBSCAN的方法(cluster_method='dbscan')或者[1]中提出的自动技术(cluster_method='xi')来提取。
这个实现与原始的OPTICS不同之处在于,它首先在所有点上执行k最近邻搜索以识别核心大小,然后在构建聚类顺序时仅计算与未处理点的距离。请注意,我们没有使用堆来管理扩展候选者,因此时间复杂度为O(n^2)。
详细信息请参阅[用户指南
参数:
min_samples:int > 1 或介于 0 和 1 之间的浮点数,默认为 5。考虑一个点为核心点的邻域中的样本数。同时,陡峭区域的上下点不能有超过min_samples个连续的非陡峭点。表达为绝对数量或样本数量的分数(至少为2)。max_eps:float,默认为 np.inf。两个样本被认为在彼此邻域中的最大距离。np.inf的默认值将识别所有尺度上的聚类;减小max_eps将导致更短的运行时间。metric:str 或可调用对象,默认为 'minkowski'。用于距离计算的度量。可以使用scikit-learn或scipy.spatial.distance中的任何度量。p:int,默认为 2。Minkowski距离的参数。当p = 1时,相当于使用曼哈顿距离(l1),当p = 2时,相当于使用欧氏距离(l2)。对于任意p,将使用Minkowski距离(l_p)。metric_params:字典,默认为 None。度量函数的附加关键字参数。cluster_method:str,默认为 'xi'。用于使用计算的可达性和排序提取聚类的提取方法。可能的值为 "xi" 和 "dbscan"。eps:float,默认为 None。两个样本被认为在彼此邻域中的最大距离。默认情况下,它假定与max_eps相同的值。仅在cluster_method='dbscan'时使用。xi:介于 0 和 1 之间的浮点数,默认为 0.05。确定达到性图上构成聚类边界的最小陡峭度。例如,在达到性图中,上升点由从一个点到其后继的比率最多为 1-xi 定义。仅在cluster_method='xi'时使用。predecessor_correction:bool,默认为 True。根据OPTICS计算的前任来修正聚类[2]。这个参数对大多数数据集的影响很小。仅在cluster_method='xi'时使用。min_cluster_size:int > 1 或介于 0 和 1 之间的浮点数,默认为 None。OPTICS聚类中的最小样本数,表示为绝对数量或样本数量的分数(至少为2)。如果为None,则使用min_samples的值。仅在cluster_method='xi'时使用。algorithm:{'auto', 'ball_tree', 'kd_tree', 'brute'},默认为 'auto'。用于计算最近邻居的算法。leaf_size:int,默认为 30。传递给BallTree或KDTree的叶子大小。这可能会影响构建和查询的速度,以及存储树所需的内存。最佳值取决于问题的性质。n_jobs:int,默认为 None。运行最近邻搜索的并行作业数。None表示使用1个处理器,除非在joblib.parallel_backend上下文中。-1表示使用所有处理器。
属性:
labels_:形状为 (n_samples,) 的数组。给定给fit()的数据集中每个点的聚类标签。噪声样本和不包括在cluster_hierarchy_的叶簇中的点标记为 -1。reachability_:形状为 (n_samples,) 的数组。每个样本的可达性距离,由对象顺序索引。使用clust.reachability_[clust.ordering_]来按簇顺序访问。ordering_:形状为 (n_samples,) 的数组。样本索引的簇排序列表。core_distances_:形状为 (n_samples,) 的数组。每个样本变为核心点的距离,由对象顺序索引。永远不会成为核心的点的距离为inf。使用clust.core_distances_[clust.ordering_]来按簇顺序访问。predecessor_:形状为 (n_samples,) 的数组。样本从中到达的点,由对象顺序索引。种子点的前任为 -1。cluster_hierarchy_:形状为 (n_clusters, 2) 的数组。每行表示簇的形式为[start, end],所有索引都是包容的。簇根据(end, -start)(升序)排序,以便较大的簇包含在较小的簇之后。由于labels_不反映层次结构,通常len(cluster_hierarchy_) > np.unique(optics.labels_)。请注意,这些索引是ordering_的,即X[ordering_][start:end + 1]形成一个簇。仅在cluster_method='xi'时可用。
[1] Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. "OPTICS: ordering points to identify the clustering structure." ACM SIGMOD Record 28, no. 2 (1999): 49-60.
[2] Schubert, Erich, Michael Gertz. "Improving the Cluster Structure Extracted from OPTICS Plots." Proc. of the Conference "Lernen, Wissen, Daten, Analysen" (LWDA) (2018): 318-329.