2021年第十二届蓝桥杯(C/C++ 大学B组)
有问题的直接评论就可以了,我随时看的到!
一、卡片(5分)
题目描述:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝有很多数字卡片,每张卡片上都是数字 0 0 0 到 9 9 9。 小蓝准备用这些卡片来拼一些数,他想从 1 1 1 开始拼出正整数,每拼一个, 就保存起来,卡片就不能用来拼其它数了。 小蓝想知道自己能从 1 1 1 拼到多少。 例如,当小蓝有 30 30 30 张卡片,其中 0 0 0 到 9 9 9 各 3 3 3 张,则小蓝可以拼出 1 1 1 到 10 10 10, 但是拼 11 11 11 时卡片 1 1 1 已经只有一张了,不够拼出 11 11 11。 现在小蓝手里有 0 0 0 到 9 9 9 的卡片各 2021 2021 2021 张,共 2021 2021 2021 张,请问小蓝可以从 1 1 1 拼到多少? 提示:建议使用计算机编程解决问题
- 我们利用哈希表来存储各个卡片的数量
- 每次对枚举的数进行分解,并且减小其所对应的卡片数量
- 当卡片数量不够时,输出答案~
C++代码
#include 正确答案: 3181 ! \color{RED}{3181}! 3181!
二、空间(5分)
题目描述:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝准备用 256 M B 256MB 256MB 的内存空间开一个数组,数组的每个元素都是 32 32 32 位 二进制整数,如果不考虑程序占用的空间和维护内存需要的辅助空间,请问 256 M B 256MB 256MB 的空间可以存储多少个 32 32 32 位二进制整数?
- 因为 1 M = ( 1024 ∗ 1024 ) B 1M=(1024*1024)B 1M=(1024∗1024)B
- 而 1 B = 8 b i t 1B=8bit 1B=8bit,所以每个元素所占的空间为 4 B 4B 4B
- 故 256 M 256M 256M能存储 256 ∗ 1024 ∗ 1024 / 4 256*1024*1024/4 256∗1024∗1024/4。
C++ 代码
#include 正确答案: 67108864 ! \color{Red}{67108864}! 67108864!
三、直线(10分)
题目描述:
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上, 那么这些点中任意两点确定的直线是同一条。
给定平面上 2 × 3 2 × 3 2×3 个整点 ( x , y ) ∣ 0 ≤ x < 2 , 0 ≤ y < 3 , x ∈ Z , y ∈ Z ( x , y ) ∣ 0 ≤ x < 2 , 0 ≤ y < 3 , x ∈ Z , y ∈ Z {(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z}(x,y)∣0≤x<2,0≤y<3,x∈Z,y∈Z (x,y)∣0≤x<2,0≤y<3,x∈Z,y∈Z(x,y)∣0≤x<2,0≤y<3,x∈Z,y∈Z,即横坐标 是 0 0 0 到 1 1 1 (包含 0 0 0 和 1 1 1) 之间的整数、纵坐标是 0 0 0 到 2 2 2 (包含 0 0 0 和 2 2 2) 之间的整数 的点。这些点一共确定了 11 11 11 条不同的直线。
给定平面上 20 × 21 20 × 21 20×21 个整点 ( x , y ) ∣ 0 ≤ x < 20 , 0 ≤ y < 21 , x ∈ Z , y ∈ Z ( x , y ) ∣ 0 ≤ x < 20 , 0 ≤ y < 21 , x ∈ Z , y ∈ Z {(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z}(x,y)∣0≤x<20,0≤y<21,x∈Z,y∈Z (x,y)∣0≤x<20,0≤y<21,x∈Z,y∈Z(x,y)∣0≤x<20,0≤y<21,x∈Z,y∈Z,即横 坐标是 0 0 0 到 19 19 19 (包含 0 0 0 和 19 19 19) 之间的整数、纵坐标是 0 0 0 到 20 20 20 (包含 0 0 0 和 20 20 20) 之 间的整数的点。
请问这些点一共确定了多少条不同的直线。
- 首先枚举一下 0 ≤ x < 20 , 0 ≤ y < 21 0 ≤ x < 20, 0 ≤ y < 21 0≤x<20,0≤y<21中的所有点,斜率不存在的点先跳过,最后特判,存入到 l l l数组中去
- 对 l l l数组的值进行排序,当斜率不等时,按照斜率的升序排列,当斜率相等时,按照截距的升序排列!
- 最后比较一下每相邻的两个直线的斜率和截距,若其中一个不相等,则证明两条直线不是同一条直线~
C++代码
#include 正确答案: 40257 ! \color{Red}{40257}! 40257!
四、货物摆放(10分)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有 n n n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L L L、 W W W、 H H H 的货物,满足 n = L × W × H n = L \times W \times H n=L×W×H。
给定 n n n,请问有多少种堆放货物的方案满足要求。
例如,当 n = 4 n = 4 n=4 时,有以下 6 6 6 种方案: 1 × 1 × 4 、 1 × 2 × 2 、 1 × 4 × 1 、 2 × 1 × 2 、 2 × 2 × 1 、 4 × 1 × 1 1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 ×1×1 1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1。
请问,当 n = 2021041820210418 n = 2021041820210418 n=2021041820210418 (注意有 16 16 16 位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
- 实际上就是找出 n n n所有的约数,存入数组 d d d中
- 然后遍历3次( i , j , k i,j,k i,j,k)找出, d ( i ) ∗ d ( j ) ∗ d ( k ) = = n d(i)*d(j)*d(k)==n d(i)∗d(j)∗d(k)==n,的所有值~
C++代码
#include 正确答案: 2430 ! \color{Red}{2430}! 2430!
五、路径(15分)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图 中的最短路径。
小蓝的图由 2021 2021 2021 个结点组成,依次编号 1 1 1 至 2021 2021 2021。
对于两个不同的结点 a a a, b b b,如果 a a a 和 b b b 的差的绝对值大于 21 21 21,则两个结点 之间没有边相连;如果 a a a 和 b b b 的差的绝对值小于等于 21 21 21,则两个点之间有一条 长度为 a a a 和 b b b 的最小公倍数的无向边相连。
例如:结点 1 1 1 和结点 23 23 23 之间没有边相连;结点 3 3 3 和结点 24 24 24 之间有一条无 向边,长度为 24 24 24;结点 15 15 15 和结点 25 25 25 之间有一条无向边,长度为 75 75 75。
请计算,结点 1 1 1 和结点 2021 2021 2021 之间的最短路径长度是多少。
提示:建议使用计算机编程解决问题。
- 我们这里可以采用多种方法求得最短路径:由于本题没有负权边,故此采用Dijkstra算法
- 我们先将所有符合要求的结点存入邻接表中
- 直接跑一遍Dijkstra算法即可得到答案
C++代码
#include 正确答案: 10266837 ! \color{Red}{10266837}! 10266837!
六、时间显示(15分)
题目描述
小蓝要和朋友合作开发一个时间显示的网站。
在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 1970 1970 1970 年 1 1 1 月 1 1 1 日 00 : 00 : 00 00:00:00 00:00:00 到当前时刻经过的毫秒数。
现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。
给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入描述
输入一行包含一个整数,表示时间。
输出描述
输出时分秒表示的当前时间,格式形如 HH:MM:SS,其中 HH 表示时,值为 0 0 0 到 23 23 23,MM 表示分,值为 0 0 0 到 59 59 59,SS 表示秒,值为 0 0 0 到 59 59 59。时、分、秒 不足两位时补前导 0 0 0。
输入样例1:
46800999
输出样例1:
13:00:00
输入样例2:
1618708103123
输出样例2:
01:08:23
数据范围
对于所有评测用例,给定的时间为不超过 1 0 18 10^{18} 1018的正整数。
运行限制
- 最大运行时间:1s
- 最大运行内存: 512M
主要思路
- 由于题目中给的数据范围是 1 0 18 10^{18} 1018,
int所最大能表达的正整数是 2 31 + 1 2^{31} + 1 231+1,我们需要用unsigned long long存储,其最大能表示的正整数是 2 64 2^{64} 264! - 又因为 1 s = 1000 m s 1s=1000ms 1s=1000ms, 1 m i n = 60 s 1min=60s 1min=60s, 1 h = 60 m i n 1h=60min 1h=60min,设给的正整数是 x x x
- 所以
h = (x / 1000 / 60 / 60) % 24同时让x -= h * 3600 * 1000 m = x / 1000 / 60 % 60,同时让x -= m * 60000;s = x / 1000 % 60
C++代码
#include 七、砝码称重(20分)
题目描述
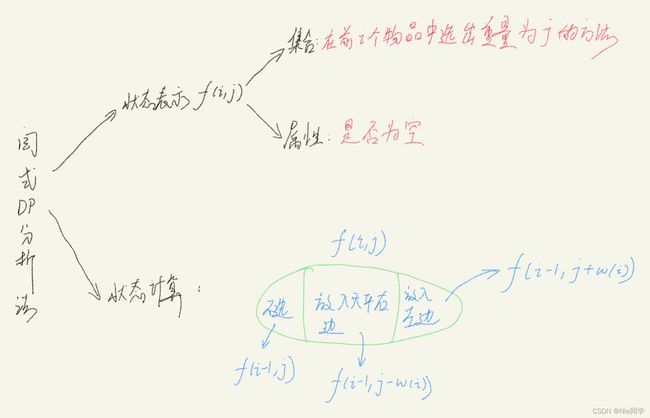
你有一架天平和 N N N 个砝码,这 N N N 个砝码重量依次是 W 1 , W 2 , ⋅ ⋅ ⋅ , W N W_1, W_2, · · · , W_N W1,W2,⋅⋅⋅,WN 。
请你计算一共可以称出多少种不同的重量? 注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 N N N。
第二行包含 N N N 个整数: W 1 , W 2 , W 3 , ⋅ ⋅ ⋅ , W N 。 W_1, W_2, W_3, · · · , W_N。 W1,W2,W3,⋅⋅⋅,WN。
输出格式
输出一个整数代表答案。
输入样例:
3
1 4 6
输出样例:
10
样例说明
能称出的 10 10 10 种重量是: 1 、 2 、 3 、 4 、 5 、 6 、 7 、 9 、 10 、 11 1、2、3、4、5、6、7、9、10、11 1、2、3、4、5、6、7、9、10、11。
1 = 1 ; 1 = 1; 1=1;
2 = 6 − 4 2 = 6 − 4 2=6−4 (天平一边放 6 6 6,另一边放 4 4 4);
3 = 4 − 1 ; 3 = 4 − 1; 3=4−1;
4 = 4 ; 4 = 4; 4=4;
5 = 6 − 1 ; 5 = 6 − 1; 5=6−1;
6 = 6 ; 6 = 6; 6=6;
7 = 1 + 6 ; 7 = 1 + 6; 7=1+6;
9 = 4 + 6 − 1 ; 9 = 4 + 6 − 1; 9=4+6−1;
10 = 4 + 6 ; 10 = 4 + 6; 10=4+6;
11 = 1 + 4 + 6 。 11 = 1 + 4 + 6。 11=1+4+6。
数据范围
-
对于 50 % 50\% 50%的评测用例, 1 ≤ N ≤ 15 1 ≤ N ≤ 15 1≤N≤15。
-
对于所有评测用例, 1 ≤ N ≤ 100 1 ≤ N ≤ 100 1≤N≤100, N N N个砝码总重不超过 100000 100000 100000。
主要思路
C++代码
#include 八、杨辉三角形(20分)
题目描述
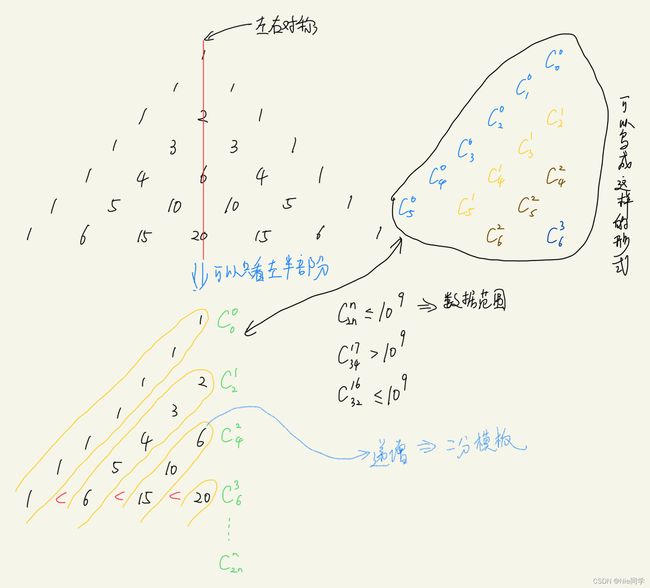
下面的图形是著名的杨辉三角形:
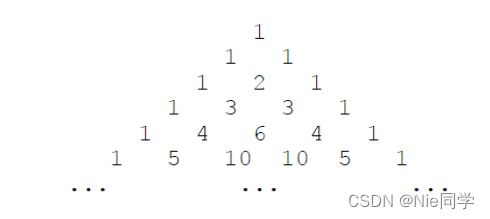
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列: 1 , 1 , 1 , 1 , 2 , 1 , 1 , 3 , 3 , 1 , 1 , 4 , 6 , 4 , 1 , ⋯ 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,\cdots 1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯
给定一个正整数 N N N,请你输出数列中第一次出现 N N N 是在第几个数?
输入描述
输入一个整数 N N N。
输出描述
输出一个整数代表答案。
输入样例
6
输出样例
13
数据范围
对于 20 % 20\% 20% 的评测用例, 1 ≤ N ≤ 10 1\leq N\leq 10 1≤N≤10; 对于所有评测用例, 1 ≤ N ≤ 1000000000 1≤N≤1000000000 1≤N≤1000000000。
主要思路
C++代码
#include 九、双向排序(25分)
题目描述
给定序列 ( a 1 , a 2 , ⋅ ⋅ ⋅ , a n ) = ( 1 , 2 , ⋅ ⋅ ⋅ , n ) (a_1, a_2, · · · , a_n) =(1,2,⋅⋅⋅,n) (a1,a2,⋅⋅⋅,an)=(1,2,⋅⋅⋅,n),即 a i = i a_i = i ai=i小蓝将对这个序列进行 m m m 次操作,每次可能是将 a 1 , a 2 , ⋯ , a q i a_1, a_2,\cdots ,a_{q_i} a1,a2,⋯,aqi降序排列,或者将 a q i , a q i + 1 , ⋯ , a n a_{q_i}, a_{q_{i+1}},\cdots , a_n aqi,aqi+1,⋯,an升序排列。
请求出操作完成后的序列。
输入描述
输入的第一行包含两个整数 n , m n, m n,m,分别表示序列的长度和操作次数。
接下来 m m m 行描述对序列的操作,其中第 i i i 行包含两个整数 p i , q i p_i, q_i pi,qi表示操作类型和参数。当 p i = 0 p_i = 0 pi=0 时,表示将 a 1 , a 2 , ⋅ ⋅ ⋅ , a q i a_1, a_2, · · · , a_{q_i} a1,a2,⋅⋅⋅,aqi降序排列;当 p i = 1 p_i = 1 pi=1时,表示将 a q i , a q i + 1 , ⋯ , a n a_{q_i} , a_{q_{i+1}}, \cdots, a_n aqi,aqi+1,⋯,an升序排列。
输出描述
输出一行,包含 n n n 个整数,相邻的整数之间使用一个空格分隔,表示操作完成后的序列。
输入样例
3 3
0 3
1 2
0 2
输出样例
3 1 2
样例说明
原数列为 ( 1 , 2 , 3 ) (1, 2, 3) (1,2,3)。
第 1 1 1 步后为 ( 3 , 2 , 1 ) (3,2,1) (3,2,1)。
第 2 2 2 步后为 ( 3 , 1 , 2 ) (3, 1, 2) (3,1,2)。
第 3 3 3 步后为 ( 3 , 1 , 2 ) (3,1,2) (3,1,2)。与第 2 2 2 步操作后相同,因为前两个数已经是降序了。
数据范围
对于 30 % 30\% 30% 的评测用例, n , m ≤ 1000 n, m \leq 1000 n,m≤1000;
对于 60 % 60\% 60% 的评测用例, n , m ≤ 5000 n, m \leq 5000 n,m≤5000;
对于所有评测用例, 1 ≤ n , m ≤ 100000 , 0 ≤ p i ≤ 1 , 1 ≤ q i ≤ n 1 \leq n, m \leq 100000,0 \leq p_i \leq 1,1 \leq q_i\leq n 1≤n,m≤100000,0≤pi≤1,1≤qi≤n
算法1 ( O ( n 2 l o g n ) O(n^2logn) O(n2logn))(快速排序的思想)
给定数据范围为: 1 0 5 10^5 105,简单的算一下该算法的操作次数大概在 1.6 ∗ 1 0 11 1.6*10^{11} 1.6∗1011,C++最佳操作次数为 1 0 7 10^7 107 ~ 1 0 8 10^8 108,所以这个算法只能拿到 60 % 60\% 60%的得分~
- 采用快速排序的思想~
C++代码
#include 算法2( 时 间 复 杂 度 ≤ O ( n l o g n ) 时间复杂度\leq O(nlogn) 时间复杂度≤O(nlogn))
主题思路
-
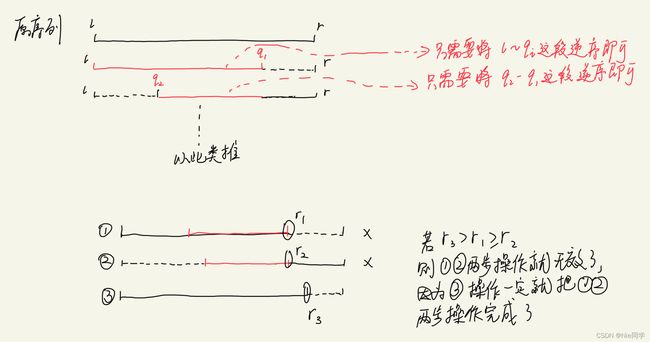
(1)如下图所示
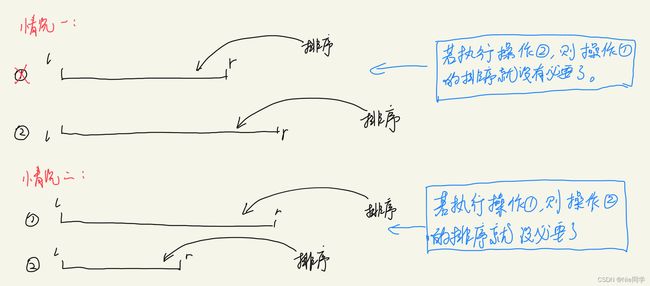
所以总的来说,如果碰到连续的同一个操作,则我们只需要保留最长的那一段即可~,所以造就了我们最后存储的操作一定是 p 1 = 0 , p 2 = 1 , p 3 = 0 , p 4 = 1 , p 5 = 0 , . . . . p_1=0,p_2=1,p_3=0,p_4=1,p_5=0,.... p1=0,p2=1,p3=0,p4=1,p5=0,....这样子的!
C++代码
#include 十、括号序列(25分)
题目描述
给定一个括号序列,要求尽可能少地添加若干括号使得括号序列变得合法,当添加完成后,会产生不同的添加结果,请问有多少种本质不同的添加结果。
两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号。
例如,对于括号序列 ( ( ( ) ((() (((),只需要添加两个括号就能让其合法,有以下几种不同的添加结果: ( ) ( ) ( ) ()()() ()()()、 ( ) ( ( ) ) ()(()) ()(())、 ( ( ) ) ( ) (())() (())()、 ( ( ) ( ) ) (()()) (()()) 和 ( ( ( ) ) ) ((())) ((()))。
输入描述
输入一行包含一个字符串 s s s,表示给定的括号序列,序列中只有左括号和右括号。
输出描述
输出一个整数表示答案,答案可能很大,请输出答案除以 1000000007 1000000007 1000000007 (即 1 0 9 + 7 10^9 + 7 109+7) 的余数。
输入样例
((()
输出样例
5
数据范围
对于 40 % 40\% 40% 的评测用例, ∣ s ∣ ≤ 200 |s| \leq 200 ∣s∣≤200。
对于所有评测用例, 1 ≤ ∣ s ∣ ≤ 5000 1 \leq |s| \leq 5000 1≤∣s∣≤5000。
主体思路
引出一个合法括号序列的两个性质
- 左右括号数相同
- 任意前缀中左括号数不小于右括号数
乘法原理
若某个对象分为 n n n个环节,第 1 1 1个环节有 m 1 m_1 m1个元素,第 2 2 2个环节有 m 2 m_2 m2个元素,……,第 n n n个环节有 m n m_n mn个元素,则该对象有 N = m 1 × m 2 × m 3 × … × m n N=m_1×m_2×m_3×…×m_n N=m1×m2×m3×…×mn 种序列,且每一个环节都相互独立。
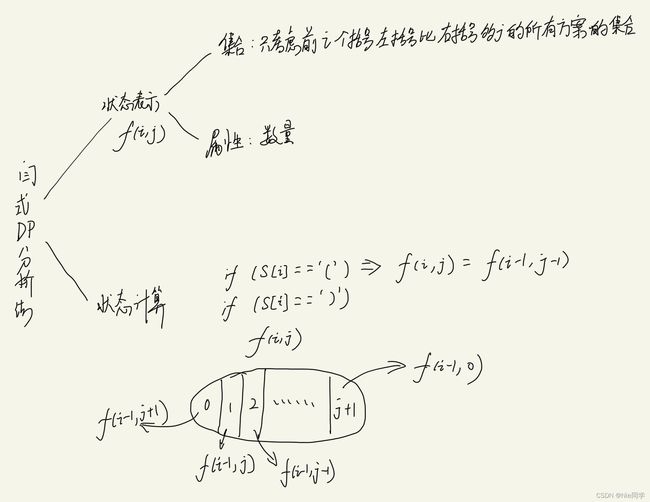
由于数据范围,所要求的时间复杂度应降到 O ( n 2 ) O(n^2) O(n2),所以我们应该进行状态的压缩
f ( i , j ) = f ( i − 1 , j + 1 ) + f ( i − 1 , j ) + f ( i − 1 , j − 2 ) + . . . + f ( i − 1 , 0 ) f(i,j)=f(i-1,j+1)+f(i - 1,j)+f(i-1,j-2)+...+f(i-1,0) f(i,j)=f(i−1,j+1)+f(i−1,j)+f(i−1,j−2)+...+f(i−1,0)
f ( i , j − 1 ) = f ( i − 1 , j ) + f ( i − 1 , j − 1 ) + f ( i − 1 , j − 2 ) + . . . + f ( i − 1 , 0 ) f(i,j-1)=f(i-1,j)+f(i-1,j-1)+f(i-1,j-2)+...+f(i-1,0) f(i,j−1)=f(i−1,j)+f(i−1,j−1)+f(i−1,j−2)+...+f(i−1,0)
所以我们可以得到: f ( i , j ) = f ( i − 1 , j + 1 ) + f ( i , j − 1 ) f(i,j)=f(i-1,j + 1)+f(i,j-1) f(i,j)=f(i−1,j+1)+f(i,j−1)使得我们的时间复杂度降低到 O ( n 2 ) O(n^2) O(n2)
C++代码
#include