多元线性回归模型（公式推导+举例应用）

引言

多元线性回归是回归分析中的一种复杂模型，它考虑了多个输入变量对输出变量的影响。与一元线性回归不同，多元线性回归通过引入多个因素，更全面地建模了系统关系。

在这篇文章中，我们将深入研究多元线性回归的原理，包括模型构建和参数估计方法。与一元线性回归相比，多元线性回归具有更高的预测和解释能力，可以更准确地捕捉各个因素对输出的复杂影响。

我们将讨论如何理解和解释多元线性回归的结果，并介绍在实际应用中如何利用这一模型进行数据分析和预测。通过深入学习多元线性回归，读者将能够更好地利用这一强大的工具，取得更准确和有力的分析结果。

模型表达式

多元线性回归模型的表达式为：$f(\mathbf{x})={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+b$
其中，$\mathbf{x}$为输入向量，包含多个特征（自变量）；$f(\mathbf{x})$为模型的输出或响应（预测的目标变量）；${\mathbf{k}}^{\mathbf{T}}$为特征权重；$b$为是模型的截距或偏置；我们的目标是通过学习${\mathbf{k}}^{\mathbf{T}}$和$b$使得$f(\mathbf{x})$尽可能的接近真实观测值$\mathbf{y}$。
为了方便计算和编程，我们可以将$b$吸收进$\mathbf{x}$和$\mathbf{k}$中去，使得$y={\hat{\mathbf{k}}}^{\mathbf{T}}\hat{\mathbf{x}}$，因为：
$$y={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+b\times 1$$
展开可得：
$$y=k_1{x}_1+k_2{x}_2+...+k_d{x}_d+b\times 1$$
我们重新令
$$\mathbf{X}=(\mathbf{x},1)=[x_1,x_2,...,x_d,1]$$
$$\hat{\mathbf{k}}=(\mathbf{k},b)=[k_1,k_2,...,k_d,b]$$
从而得到$y={\hat{\mathbf{k}}}^{\mathbf{T}}\mathbf{X}$。这样的变形使得模型表达更为简洁，同时不影响其表达能力。

均方误差和优化目标

为了衡量模型的性能，我们引入均方误差$J(\hat{\mathbf{k}}):$
$$J(\hat{\mathbf{k}})=(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}})$$
我们的优化目标是最小化均方误差，即：

$$E({\hat{\mathbf{k}}}^{\star })=ar{g}_{(\hat{\mathbf{k}})}min(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}})$$

最小二乘法

通过最小二乘法，我们对均方误差函数分别对$\hat{\mathbf{k}}$求导数，令其等于零，得到优化的解：
$$\frac{\partial }{\partial \hat{\mathbf{k}}}E(\hat{\mathbf{k}})=2{\mathbf{X}}^{\mathbf{T}}(\mathbf{X}\hat{\mathbf{k}}-\mathbf{y})=0$$
整理并得到：

• 若${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$为满秩矩阵或正定矩阵直接令$\frac{\partial }{\partial \hat{\mathbf{k}}}E(\hat{\mathbf{k}})=0$可得到：
  $${\hat{\mathbf{k}}}^{\star }=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$
  最终得到多元线性回归模型：
  $$f({\hat{\mathbf{y}}}_{\mathbf{i}})={\hat{\mathbf{x}}}_{\mathbf{i}}({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$
• 若${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$不是满秩矩阵，则会有无穷多解，此时可以解出多个$\hat{\mathbf{k}}$都能使得均方误差最小化。选择哪一个，将由学习算法的归纳偏好决定，常见的做法是引入正则化项。
  • 二分类分类任务：对数几率回归。
  • 回归任务：对数线性回归、岭回归、套索回归等。

广义线性模型

我们可以把线性模型简写为：
$$\mathbf{y}={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+b$$
若模型假设因变量（或称响应变量）的自然对数与自变量之间存在线性关系。通常，对数线性回归的模型可以写成：
$$ln\mathbf{y}={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+b$$
现在我们算
$$\mathbf{y}=e^{{\mathbf{k}}^{\mathbf{T}}\mathbf{x}+\mathbf{b}}$$
实际上是通过$e^{{\mathbf{k}}^{\mathbf{T}}\mathbf{x}+\mathbf{b}}$来逼近$\mathbf{y}$，在形式上$ln\mathbf{y}={\mathbf{k}}^{\mathbf{T}}\mathbf{x}+b$仍然是线性回归。
更一般的考虑任意单调可微函数$g(\cdot )$，令
$$y=g^{-1}(k^{T}x+b)$$
其中函数$g(\cdot )$称为联系函数，$g^{-1}(\cdot )$为$g$的反函数，显然对数线性回归是一种广义线性模型的特例。

范数

在数学和函数空间理论中，范数是对向量空间中的向量进行度量或测量的一种方法。范数满足一些基本的性质，通常表示为$\Vert \mathbf{v}\Vert$ ，其中$\mathbf{v}$是向量。
一般来说，一个范数是一个非负的标量函数，对于每个向量$\mathbf{v}$ ，满足以下条件：

1. 非负性：$\Vert \mathbf{v}\Vert \ge 0$，且等号仅在$\mathbf{v}=0$时成立。
2. 齐次性（或者称为尺度不变性）： 对于任意标量$\alpha$，有$\Vert \alpha \mathbf{v}\Vert =|\alpha |\Vert \mathbf{v}\Vert$
3. 三角不等式： 对于任意两个向量$\mathbf{v}$和$\mathbf{w}$，有$\Vert \mathbf{v}+\mathbf{w}\Vert \le \Vert \mathbf{v}\Vert +\Vert \mathbf{w}\Vert$
   常见的范数包括：

• $L_1$范数（曼哈顿范数）：$\Vert \mathbf{v}{\Vert }_1={\sum }_{i=1}^n\left|v_i\right|$，表示向量元素的绝对值之和。
• $L_2$范数（欧几里德范数）：$\Vert \mathbf{v}{\Vert }_2=\sqrt{{\sum }_{i=1}^n{v}_i^2}$，表示向量元素的平方和的平方根。
• $L_p$范数：$\Vert \mathbf{v}{\Vert }_p={\left({\sum }_{i=1}^n{\left|v_i\right|}^p\right)}^{1/p}$，其中$p\ge 1$。
• 无穷范数：$\Vert \mathbf{v}{\Vert }_{\infty }={\max }_i\left|v_i\right|$，表示向量元素的最大绝对值。
  在机器学习和优化问题中，范数常常用于表示向量的大小或稀疏性，同时也在正则化项中经常出现。

${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$不是满秩情况下，回归问题的解决方案

岭回归

岭回归是一种用于处理多重共线性问题的线性回归方法。多重共线性指的是自变量之间存在高度相关性的情况，这可能导致普通最小二乘法估计的不稳定性和过拟合问题。岭回归通过在损失函数中引入正则化项，有效地解决了这些问题。
岭回归的优化目标是最小化以下损失函数：
$$L(\hat{\mathbf{k}})=(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}})+\alpha \Vert \hat{\mathbf{k}}{\Vert }_2^2$$
其中$\alpha$是岭回归引入的正则化参数，正则化项$\alpha \Vert \hat{\mathbf{k}}{\Vert }_2^2$是$L_2$范式的平方，也称为岭回归的平方惩罚。它惩罚回归系数的平方和，使得系数趋向于较小的值，从而减缓过拟合问题。
最小化损失函数的解可以通过对损失函数关于$\hat{\mathbf{k}}$的梯度等于零来得到。令梯度为零，得到岭回归的正规方程：
$$\left({\mathbf{X}}^T\mathbf{X}+\alpha \mathbf{E}\right)\hat{\mathbf{k}}={\mathbf{X}}^T\mathbf{y}$$

岭回归的解可以通过以下方式得到：
$${\hat{\mathbf{k}}}^{\star }={\left({\mathbf{X}}^T\mathbf{X}+\alpha \mathbf{E}\right)}^{-1}{\mathbf{X}}^T\mathbf{y}$$
其中$|{\mathbf{X}}^T\mathbf{X}|=0$，那么$|{\mathbf{X}}^T\mathbf{X}+\alpha \mathbf{E}|\ne 0$，故可知$({\mathbf{X}}^T\mathbf{X}+\alpha \mathbf{E})$可逆。
最终得到多元线性回归模型：
$$f({\hat{\mathbf{y}}}_{\mathbf{i}})={\hat{\mathbf{x}}}_{\mathbf{i}}{\left({\mathbf{X}}^T\mathbf{X}+\alpha \mathbf{E}\right)}^{-1}{\mathbf{X}}^T\mathbf{y}$$

套索回归

套索回归是一种用于处理线性回归模型的正则化方法，类似于岭回归。套索回归通过在损失函数中引入$L_1$范数正则化项，有助于推动回归系数向零，从而实现特征的稀疏性（某些特征的系数变为零）。
套索回归的优化目标是最小化以下损失函数：
$$L(\hat{\mathbf{k}})=(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}})+\alpha \Vert \hat{\mathbf{k}}{\Vert }_1$$
其中$\alpha$是套索回归引入的正则化参数，用于控制正则化项的强度，正则化项$\alpha \Vert \hat{\mathbf{k}}{\Vert }_1$是$L_1$范式，也称为套索回归的绝对值惩罚。它通过对回归系数的绝对值求和来推动系数向零。由于$L_1$范数惩罚的特性，套索回归有助于实现特征的选择，即某些特征的系数变为零，从而达到降维和特征稀疏性的效果。
套索回归的解可以通过最小化损失函数来获得。通过对损失函数关于$\hat{\mathbf{k}}$的梯度等于零，得到套索回归的正规方程：
$$-\frac{1}{n}{\mathbf{X}}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{k}})+\alpha \cdot \mathrm{sign}(\hat{\mathbf{k}})=0$$
其中$\mathrm{sign}(\hat{\mathbf{k}})$是回归系数的符号函数。套索回归的解通常需要通过迭代方法（如坐标下降法）求解，因为没有直接的解析解。因为$L_1$范数的非光滑性质，使得套索回归的优化问题不是光滑凸优化问题，梯度下降法并不是直接适用的方法。

弹性网络回归（Elastic Net）

Elastic Net是套索回归和岭回归的组合，它同时使用$L_1$和$L_2$正则化项。Elastic Net的损失函数可以写成：
$$\mathrm{Loss}=\mathrm{MSE}+\alpha \cdot \left(\rho \cdot \sum _{i=1}^n\left|w_i\right|+\frac{1-\rho }{2}\cdot \sum _{i=1}^n{w}_i^2\right)$$
其中：

• $MSE$是均方误差的损失函数，$\mathrm{MSE}=\frac{1}{m}{\sum }_{i=1}^m{\left(y_i-{\hat{y}}_i\right)}^2$；
• $w_i$是模型的权重。
• $\alpha$是总的正则化强度，控制整体正则化的程度。
• $\rho$是$L_1$正则化项的比例，取值范围在0到1之间，控制$L_1$和$L_2$正则化项的权重比例。

Elastic Net的优势在于：

综合$L_1$和$L_2$正则化的优点： Elastic Net同时考虑到$L_1$和$L_2$正则化的特点，可以在存在高度相关特征的情况下保持$L_2$正则化的稳定性，并利用$L_1$正则化进行特征选择。
处理多重共线性： 当数据集中存在多个高度相关的特征时，Elastic Net相对于套索回归具有更好的稳定性。

${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$不是满秩情况下，二分类问题的解决方案

对数几率回归

对数几率回归是一种用于解决二分类问题的统计学习方法。尽管名字中包含"回归"，但实际上它是一种分类算法，用于估计某个样本属于某个类别的概率。对数几率回归的基本原理是基于线性回归的形式，但通过使用对数几率函数将线性输出映射到概率空间。
对数几率回归的模型表达式如下：
$$P(Y=1\mid \mathbf{X})=\frac{1}{1+e^{-(\mathbf{X}\hat{k}+b)}}$$
其中$P(Y=1\mid \mathbf{X})$是给定输入特征$\mathbf{X}$条件下样本属于类别1的概率。
对数几率函数$f(z)=\frac{1}{1+e^{-z}}$被称为sigmoid函数，用于将线性组合$\mathbf{X}\hat{k}+b$映射到0到1之间的概率值。
考虑二分类问题，设观测到的数据集为$\left\{\left({\mathbf{x}}_1,y_1\right),\left({\mathbf{x}}_2,y_2\right),\dots ,\left({\mathbf{x}}_n,y_n\right)\right\}$，其中${\mathbf{x}}_{\mathbf{i}}$是输入特征，${\mathbf{y}}_{\mathbf{i}}$是类别标签（0或1），对应着样本属于类别1的概率。
假设样本是独立同分布的，似然函数可以写成：
$$L(\hat{\mathbf{k}},b)=\prod _{i=1}^{n}P{\left(Y=y_i\mid {\mathbf{x}}_i\right)}^{y_i}\cdot {\left(1-P\left(Y=y_i\mid {\mathbf{x}}_i\right)\right)}^{1-y_i}$$
其中，$P\left(Y=y_i\mid {\mathbf{x}}_i\right)$是对数几率函数。
为了方便计算，通常对似然函数取对数，得到对数似然函数：
$$\ell (\hat{\mathbf{k}},b)=\sum _{i=1}^n\left[y_i\log \left(P\left(Y=1\mid {\mathbf{x}}_i\right)\right)+\left(1-y_i\right)\log \left(1-P\left(Y=1\mid {\mathbf{x}}_i\right)\right)\right]$$
极大似然估计的目标是最大化对数似然函数。通常使用梯度下降等优化算法来找到能最大化对数似然函数的参数$\hat{\mathbf{k}}$和$b$。
令$\beta =(\hat{\mathbf{k}},b)$对数几率回归的优化问题可以写成：
$${\beta }^{\star }=ar{g}_{(\beta )}min\ell (\beta )$$

• 梯度下降法求解${\beta }^{\star }$：$\beta \leftarrow \beta -\alpha \nabla \ell (\beta )$其中，$\alpha$为学习率，$\nabla \ell (\beta )$是对数似然函数关于$\beta$的梯度。
• 牛顿法求解${\beta }^{\star }$：$\beta \leftarrow \beta -H^{-1}\nabla \ell (\beta )$，其中$\nabla \ell (\beta )$是对数似然函数关于$\beta$的梯度，$H$是对数似然函数关于$\beta$的黑塞矩阵。

黑塞矩阵

黑塞矩阵是一个包含一个标量函数的二阶偏导数的方块矩阵。对于一个具有多个变量的标量函数，黑塞矩阵包含该函数的所有二阶偏导数信息。在优化算法中，黑塞矩阵通常用于描述目标函数的曲率。
对于一个具有$n$个变量的标量函数$f(x)$，其中$\mathbf{x}=[x_1,x_2,...,x_n]$是变量向量，黑塞矩阵$H$的元素为：
$$H_{ij}=\frac{{\partial }^{2}f}{\partial x_i\partial x_j}$$
黑塞矩阵的维度是$n\times n$，其中$n$是变量的数量。
在数学和优化理论中，黑塞矩阵提供了目标函数的局部二阶导数信息。对于优化算法，特别是牛顿法，黑塞矩阵被用于调整参数的更新步长，以更有效地收敛到函数的局部极小值。

在对数几率回归中，黑塞矩阵描述了对数似然函数的曲率，它的使用通常是为了加速收敛并提高算法的稳定性。然而，计算和存储大型黑塞矩阵可能会带来计算复杂性，因此在实际应用中，可能会使用黑塞矩阵的逆矩阵的近似值，或者采用拟牛顿方法。

结论

本文全面探讨了多元线性回归及其在非满秩矩阵情况下的解决方案。广义线性模型的引入以及岭回归、套索回归的讨论进一步增强了对多元线性回归的理解和应用。对数几率回归作为处理非满秩矩阵的二分类问题的解决方案，为实际应用提供了有效的工具。总体而言，本文为读者提供了深入学习多元线性回归的基础，并为实际数据分析和预测提供了有力支持。

实验分析（一）

${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$满秩情况
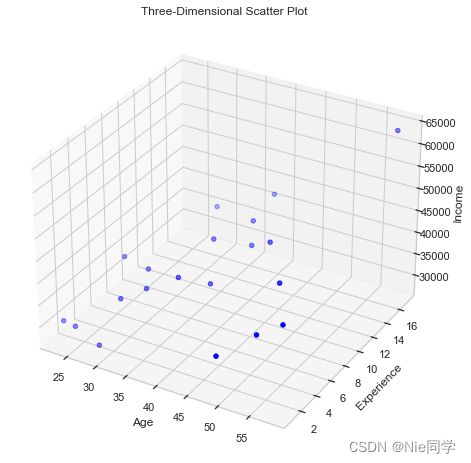
以下是工人工作年限、年龄与对应薪水的数据集。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="deep")
# 读入数据集
data = pd.read_csv('data/multiple_linear_regression_dataset.csv')
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 提取数据
age = data['age']
experience = data['experience']
income = data['income']

# 绘制三维散点图
ax.scatter(age, experience, income, c='blue', marker='o', label='Data Points')

# 添加标签和标题
ax.set_xlabel('Age')
ax.set_ylabel('Experience')
ax.set_zlabel('Income')
ax.set_title('Three-Dimensional Scatter Plot')

# 显示图形
plt.show()

将$b$吸收进$\mathbf{x}$和$\mathbf{k}$中去，使得$y={\hat{\mathbf{k}}}^{\mathbf{T}}\hat{\mathbf{x}}$

# 提取 x 向量和 y 向量
X = data[['age', 'experience']]
X['bias'] = 1  # 添加额外的 1 列
Y = data['income']

判断${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$是否满秩。

# 判断X.T * X是否是满秩矩阵
print(np.linalg.matrix_rank(X.T @ X) == min(X.shape[0], X.shape[1]))

输出结果：True，说明${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$满秩，故直接有：
$${\hat{\mathbf{k}}}^{\star }=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$

# 计算参数
k = np.linalg.inv(X.T @ X) @ X.T @ Y

计算得出：$k_1=-99.195355$，$k_2=2162.404192$，$b=31261.689854$。
故直线方程为$y=-99.195355x_1+2162.404192x_2+31261.689854$。

画出拟合曲线图

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import numpy as np

# 定义直线方程
def linear_equation(age, experience):
    return k[0] * age + k[1] * experience + k[2]

# 选择一部分数据进行绘制
sample_size = min(50, len(age))  # 选择样本数量为50或总体数量的最小值
sample_indices = np.random.choice(len(age), size=sample_size, replace=False)

# 创建三维图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制散点图，调整透明度和颜色映射
scatter = ax.scatter(age[sample_indices], experience[sample_indices], income[sample_indices], c=income[sample_indices], cmap='viridis', marker='o', s=80, alpha=0.6, label='Data Points', zorder=2)

# 生成一些数据点用于绘制，调整曲面高度
age_points = np.linspace(20, 60, 200)
experience_points = np.linspace(0, 20, 200)
age_grid, experience_grid = np.meshgrid(age_points, experience_points)
income_pred = linear_equation(age_grid, experience_grid)

# 绘制曲面，调整透明度
ax.plot_trisurf(age_grid.flatten(), experience_grid.flatten(), income_pred.flatten(), cmap='viridis', alpha=0.2, linewidth=0, zorder=1)

# 设置轴标签
ax.set_xlabel('Age')
ax.set_ylabel('Experience')
ax.set_zlabel('Income')

# 调整视角
ax.view_init(elev=40, azim=30)

# 显示图例
ax.legend(handles=[scatter], labels=['Data Points'], loc='upper left')

# 显示图形
plt.show()

实验分析（二）

${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$满秩情况，且是回归问题。
以下数据集是房屋面积、房间数、卧室数量、浴室数量、车库空间、建造年份对应价格的数据集。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="deep")

# 读入数据集
data = pd.read_csv('data/predict_room_price.csv')

我们规定前4500条数据是训练集、后500条数据是测试集。

# 划分训练集和测试集
train_data = data.iloc[:4500, :]
test_data = data.iloc[4500:, :]

# 提取训练集的 x 向量和 y 向量
X_train = train_data.iloc[:, :-1]
X_train['bias'] = 1  # 添加额外的 1 列
Y_train = train_data['Price']

# 提取测试集的 x 向量和 y 向量
X_test = test_data.iloc[:, :-1]
X_test['bias'] = 1  # 添加额外的 1 列
Y_test = test_data['Price']

并且判断${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$，输出结果：Is X_train.T * X_train full rank? False，不满秩！

# 判断 X_train.T * X_train 是否是满秩矩阵
is_full_rank_train = np.linalg.matrix_rank(X_train.T @ X_train) == min(X_train.shape[0], X_train.shape[1])
print("Is X_train.T * X_train full rank?", is_full_rank_train)

• 使用岭回归

# 如果不是满秩，使用岭回归, 
alpha = 1.0  # 超参数，需要调整

# 计算岭回归系数
XTX_train = X_train.T @ X_train
XTY_train = X_train.T @ Y_train
identity_matrix_train = np.eye(XTX_train.shape[0])

ridge_coefficients_train = np.linalg.solve(XTX_train + alpha * identity_matrix_train, XTY_train)

得出$${\hat{\mathbf{k}}}^{\star }=[1.84627067,2.76940446,4.40065163,4.13604178,0.84099326,-0.09549601,-7.83477733]$$

# 在测试集上预测
Y_pred_test = X_test @ ridge_coefficients_train

# 画散点图比较真实值和预测值
plt.figure(figsize=(10, 6))
plt.scatter(Y_test, Y_pred_test, alpha=0.5)
plt.title('Training Set: True Values vs Predicted Values')
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.show()

散点图应该近似位于一条对角线上，说明模型性能良好。

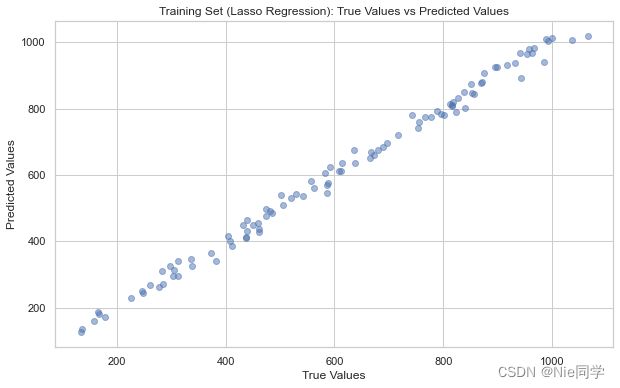
• 使用套索回归（直接调用sklearn库的Lasso回归）

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 创建套索回归模型
lasso_model = Lasso(alpha=alpha)

# 在训练集上训练套索回归模型
lasso_model.fit(X_train, Y_train)

Y_pred_test_lasso = lasso_model.predict(X_test)

# 画散点图比较真实值和预测值
plt.figure(figsize=(10, 6))
plt.scatter(Y_test, Y_pred_test_lasso, alpha=0.5)
plt.title('Training Set (Lasso Regression): True Values vs Predicted Values')
plt.xlabel('True Values')
plt.ylabel('Predicted Values')
plt.show()

最后比较一下两个策略的均方误差：

# 计算lasso测试集上的均方误差
mse_test_lasso = np.mean((Y_test - Y_pred_test_lasso)**2)
print(mse_test_lasso)

# 计算brige测试集上的均方误差
brige_test_lasso = np.mean((Y_test - Y_pred_test)**2)
print(brige_test_lasso)

mse_test_lasso=387.3594633205649
brige_test_lasso=387.9778997027562
选择套索回归还是岭回归的因素：

1. 如果你的数据集中包含许多特征，且你认为其中只有一部分特征对目标变量有显著影响，你可能更倾向于使用套索回归。
2. 如果你的数据集中存在多重共线性，即特征之间高度相关，岭回归可能更适合。
3. 实际上，有时候也可以使用 Elastic Net，它是套索回归和岭回归的结合，综合了两者的优点，但会引入额外的超参数。

• 使用Elastic Net

from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import StandardScaler

# 标准化特征
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# 初始化Elastic Net回归模型
alpha_net = 0.01
l1_ratio = 0.5  # l1_ratio 控制 L1 和 L2 的权重，可以根据需求调整
elastic_net = ElasticNet(alpha=alpha_net, l1_ratio=l1_ratio)

# 在训练集上训练模型
elastic_net.fit(X_train_scaled, Y_train)

# 在测试集上预测
Y_pred_test_net = elastic_net.predict(X_test_scaled)

# 计算测试集上的均方误差
mse_test = mean_squared_error(Y_test, Y_pred_test)
print("Mean Squared Error on Test Set (Elastic Net Regression):", mse_test)

elastic_net_lasso=385.770533673404
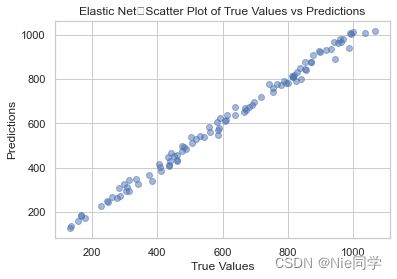
画出散点图

# 画出测试集真实值与预测值的散点图
plt.scatter(Y_test, Y_pred_test_net, alpha=0.5)
plt.xlabel("True Values")
plt.ylabel("Predictions")
plt.title("Elastic Net：Scatter Plot of True Values vs Predictions")
plt.show()

显然使用Elastic Net效果会更好。

实验分析（三）

${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$满秩情况，且是分类问题。
以下数据集是学生学习市场对应成绩（过于不过）的数据集。

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

# 读取生成的数据集
df = pd.read_csv('data\logistic_regression_dataset.csv')

# 划分特征和目标变量
X = df[['Study Hours']]
y = df['Exam Result']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建对数几率回归模型
logreg_model = LogisticRegression(random_state=42)

# 在训练集上拟合模型
logreg_model.fit(X_train, y_train)

# 预测测试集
y_pred = logreg_model.predict(X_test)

# 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f'Accuracy: {accuracy:.2f}')
print(f'Confusion Matrix:\n{conf_matrix}')
print(f'Classification Report:\n{class_report}')

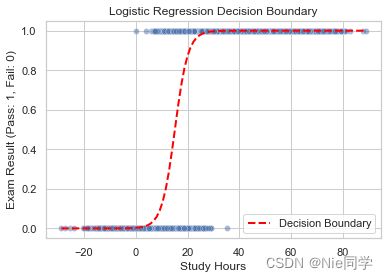
# 可视化决策边界
sns.scatterplot(x='Study Hours', y='Exam Result', data=df, alpha=0.5)
plt.xlabel('Study Hours')
plt.ylabel('Exam Result (Pass: 1, Fail: 0)')

# 绘制决策边界
x_values = np.linspace(df['Study Hours'].min(), df['Study Hours'].max(), 100)
y_values = logreg_model.predict_proba(x_values.reshape(-1, 1))[:, 1]
plt.plot(x_values, y_values, color='red', linestyle='dashed', linewidth=2, label='Decision Boundary')

plt.legend()
plt.title('Logistic Regression Decision Boundary')
plt.show()

Accuracy: 0.94
Confusion Matrix:
[[ 416   95]
 [  78 2411]]
Classification Report:
              precision    recall  f1-score   support

           0       0.84      0.81      0.83       511
           1       0.96      0.97      0.97      2489

    accuracy                           0.94      3000
   macro avg       0.90      0.89      0.90      3000
weighted avg       0.94      0.94      0.94      3000

根据提供的评估指标，该模型表现良好。

1. 准确率（Accuracy）: 0.94

• 准确率测量模型的整体正确性。
• 在这种情况下，模型正确预测了结果的百分之94。

2. 混淆矩阵:

• 真正例 (True Positives, TP): 2411
• 真负例 (True Negatives, TN): 416
• 假正例 (False Positives, FP): 95
• 假负例 (False Negatives, FN): 78

3. 分类报告：

• 精确率 (Precision, 类别 0): 84% - 所有被预测为类别 0 的实例中，有84%实际上是类别 0。
• 召回率 (Recall, 类别 0): 81% - 所有实际上是类别 0 的实例中，模型正确地预测了81%。
• F1分数 (F1-score, 类别 0): 83% - 类别 0 的精确率和召回率的调和平均数。
• 精确率 (Precision, 类别 1): 96% - 所有被预测为类别 1 的实例中，有96%实际上是类别 1。
• 召回率 (Recall, 类别 1): 97% - 所有实际上是类别 1 的实例中，模型正确地预测了97%。
• F1分数 (F1-score, 类别 1): 97% - 类别 1 的精确率和召回率的调和平均数。

4. 宏平均 / 加权平均:

• 宏平均分别计算每个类别的指标，然后取平均值。加权平均考虑每个类别的样本数。

总体而言，该模型显示出较高的准确性，对两个类别（0 和 1）的区分能力强。在两个类别上，精确率和召回率都表现良好。加权平均值表明该模型在整个数据集上具有良好的泛化能力。