C语言-贪心、回溯算法-快递终端送货分配系统

问题描述

假设某快递终端投递站，服务n个小区，小区与快递点之间有道路相连，如下图，边上的权值表示距离。

现在设有m包裹，每个包裹都有自己的目的地及总量。

1. 假设送货员一次投递的最大重量无限，设计一个把所有货物送到目的的最短路径算法。
2. 现在设一个快递员一次投递的最大重量为100kg（包裹的总重量远大于100kg), 设计一个把所有货物送到目的的跑的趟数最小的算法。
3. 设从投递点出发，投递第k包裹的总路径长度为pl，其投递代价为,设计一个把所有货物送到目的的代价最小的算法。
4. 快递员行驶速度为10km/h,快递员在一个小区的投放时间为10分钟，设计一个把所有货物送到目的的时间最少最小的算法。
5. 你还可以提出什么问题？如何解决该问题？

1.问题一

1.1方法及基本思路

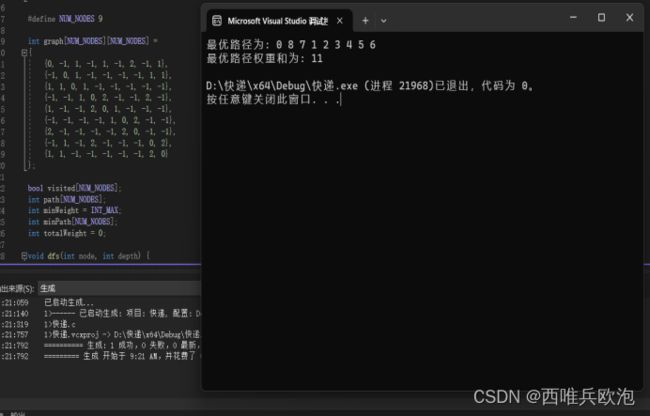
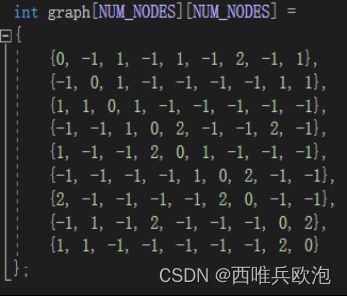
使用了深度优先搜索（DFS）算法来寻找图中的最优路径。代码中定义了一个9x9的图形状，每个节点表示图中的一个顶点，每个元素表示两个节点之间的边的权重。代码使用递归函数`dfs`来执行深度优先搜索，该函数从起始节点开始遍历图，并记录已访问的节点和当前路径的权重和。

遍历过程中，如果遍历到叶子节点（即已经访问了所有节点），则计算当前路径的权重和。如果当前路径的权重和比之前记录的最小权重和小，则更新最小权重和和最优路径。最后，在主函数中调用`dfs`函数并打印最优路径和最优路径权重和。

整个算法的基本思路是通过遍历所有可能的路径，找到权重和最小的路径作为最优路径。通过使用深度优先搜索算法，可以找到所有的路径并比较它们的权重和。代码中还包含一些边界条件的处理，例如考虑到边的权重可能为-1表示两个节点之间没有连接。

1.2数据结构描述

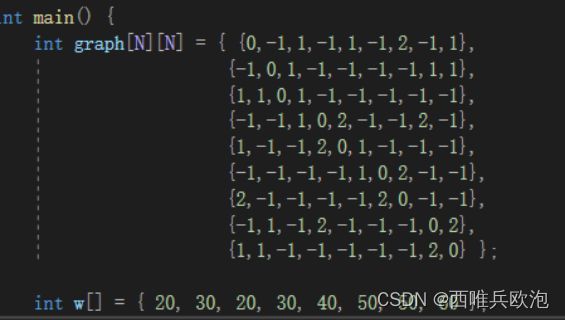
1. 二维数组`graph`：用来表示图的邻接矩阵。矩阵元素表示两个节点之间的边的权重。如果元素的值为-1，表示两个节点之间没有连接。

2. 一维数组`visited`：用来标记节点是否被访问过。初始时，所有节点都未被访问。

3. 一维数组`path`：用来保存当前路径中的节点。用于记录已经访问的节点和当前路径的权重和。

4. 变量`minWeight`和`minPath`：分别用于保存最小路径的权重和最小路径。

5. 变量`totalWeight`：用于计算每条路径的权重和。

这些数据结构用于存储和处理图的相关信息，以便执行深度优先搜索算法并找到最优路径和权重。

1.3算法描述

算法名称：深度优先搜索

输入：带权邻接矩阵

输出：最短路径以及最短路径之和

定义函数 dfs(node, depth) :

将节点 node 标记为已访问

将节点 node 添加到路径 path 的末尾

If: depth == NUM_NODES - 1：  // 到达叶子节点

    将 totalWeight 设置为0

对于 i 从 0 到 NUM_NODES - 2：

    If: graph[path[i]][path[i + 1]] == -1：

     将 totalWeight 设置为无穷大  // 不连通的路径

    跳出循环

    totalWeight += graph[path[i]][path[i + 1]]

If: totalWeight < minWeight：

     将 minWeight 设置为 totalWeight

     将 path 复制到 minPath

否则：

   对于 i 从 0 到 NUM_NODES - 1：

    If: 节点 i 未被访问 并且 graph[node][i] != 0：

     调用 dfs(i, depth + 1)

      将节点 node 标记为未访问  

1.4时间空间复杂度分析

基本运算：比较

递归公式：T(n) = (n-1) * T(n-1)

时间复杂度为：O(n！),时间复杂度比较高，不适合计算大量数据。

空间复杂度：O(n)

1.5算法实例

输入数据:

输出数据：

2.问题二

2.1方法及基本思路

给定了每次最多装100kg的物品，设计把所有货物送到目的的跑的趟数最小的算法。抽象出来就是一个0-1背包问题，其物品重量就是物品本身的重量，背包容量就是100kg，物品价值定义为单位“1”。简单来说，本问题就是如果让能装100kg的背包一次性装最多的物品。多次利用0-1背包问题即可完成该问题。

利用回溯法试设计一个算法求出0-1背包问题的解，也就是求出一个解向量。

在递归函数Backtrack中， 当i>n时，算法搜索至叶子结点，得到一个新的物品装包方案。此时算法适时更新当前的最优价值。

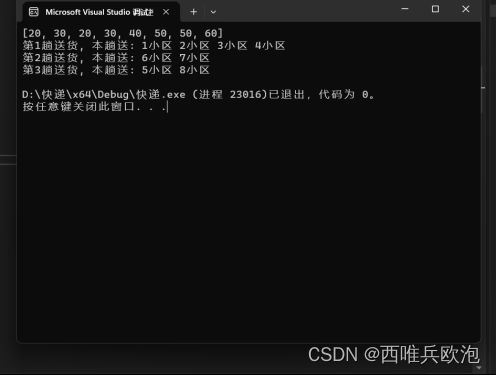
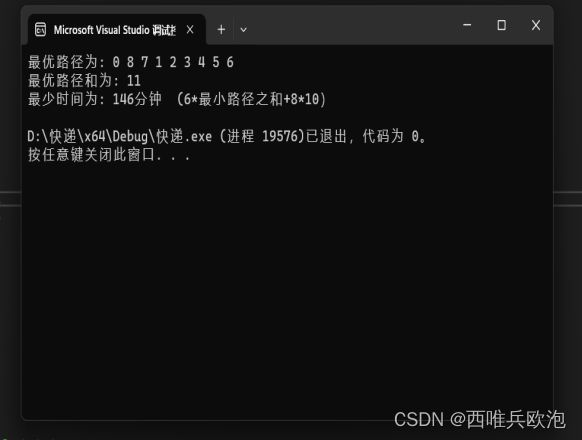
当i

设：

    take[1..n] 其中take[i] = 1，代表第i个物品要放

    take[i] = 0，代表第i个物品不放

约束条件：

    第i个物品确定放置方法后，背包所剩重量足够放第i个物品

  curW + w[i] <= bagV

   (curW为当前背包重量，w[i]为第i个物品重量，bagV为背包总重)

求最优值回溯。

2.2数据结构描述

   int w[]: 存储物品的重量（假设有9个物品，索引从1到8）

   int v[]: 存储物品的价值（假设有9个物品，索引从1到8）

   int take[]: 存储当前选择的物品，用于记录是否选取了该物品（假设有9个物品，索引从1到8）

   int bestChoice[]: 存储当前最优的物品选择

2.3算法描述

算法名称：回溯算法

Backtrack(i,n,w[1..n],v[1..n],curW,curV)

输入：从第i个物品开始

        w[i] 第i个物品重量 bastChoice[i]是否选择第i个物品

        v[i] 第i个物品价值 take[i]是否选择第i个物品

        curW 当前背包重量   curV 当前背包价值

        bagV 背包总重量 n 为物品数

输出：改变bastChoic，选择物品

if i > n bestChoice ← take

else

for i ← j to 2 do

           take[i] ← j

           if curW + w[i] <= bagV

           curW ← curW + w[i]

           curV ← curV + v[i]

           Backtrack(i+1)

           curW ← curW - w[i]

           curV ← curV - v[i]

2.4时间空间复杂度分析

基本运算：比较

递归公式：T(n) = 2 * T(n-1) + 1

T(n)表示n个物品时的递归调用次数，等于n个物品时选择物品和不选择物品两种状态的递归调用次数之和。

时间复杂度为：O(2^n),时间复杂度比较高，不适合计算大量数据。

空间复杂度为：O(n)。

计算上界Bound()函数需要O(n)时间，在最坏的情况下有O(2^n)个右子节点需要计算上界。分析问题可以发现，该回溯问题就是遍历了一颗二叉树，因此其算法复杂度就为O(2^n)。

2.5算法实例

输入数据：

输出数据：

设八个小区快递重量分别为：20kg,30kg,20kg,30kg,40kg,50kg,50kg,60kg

得到最小趟数：3趟

3.问题三

3.1方法及基本思路

设从投递点出发，投递第i包裹的总路径长度为l(i)。此题可以转换为求最小生成树，在求快递路径。使用Dijkstra算法较为简便。Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

  Dijkstra算法采用的是一种贪心的策略，声明一个数组result来保存源点到各个顶点的最短距离和一个保存已经找到了最短路径的顶点的集合：初始时，原点i的路径权重被赋为 0（result[i] = 0）。若对于顶点i存在能直接到达的边，则把result[i]设为其距离,同时把所有其他（i不能直接到达的）顶点的路径长度设为无穷大（-1）。

  从result数组选择最小值，则该值就是源点s到该值对应的顶点的最短路径，并且把该点加入然后，新加入的顶点是否可以到达其他顶点并且通过该顶点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在result中的值。

3.2数据结构描述

一维数组：

int w[]: 存储每个节点的投递代价（假设有N=9个节点），用于根据路径长度计算出投递的总代价。

二维数组：

int graph[N][N]: 用于表示邻接矩阵，存储任意两个节点之间的路径长度（假设有9个节点，索引从0到8）。-1表示两个节点之间没有路径。该数组用于计算最短路径和路径代价。

3.3算法描述

3.4时间空间复杂度分析

基本运算：比较

时间复杂度为：O(n^2)。

空间复杂度为：O(n)。

递归公式：T（n）=O(n^2)

该算法用了两层for，外层为需要访问的顶点个数，时间复杂度为O(n)，内层有两个for，第一个for为挑选未被访问的顶点的最短距离，时间复杂度为O(n)，第二个for为在与选中顶点有直接路径的顶点中对比距离是否需要更新，时间复杂度为O(n)，所以总的时间复杂度为O(n^2)。

3.5算法实例

输入数据：

输出数据：

4.问题四

4.1方法及基本思路

时间和路程问题抽象出来其实是等价的，路程越短，所花的时间也就越短，因此可以继续沿用第一问的思路，使用深度优先搜索（DFS）算法来寻找图中的最优路径。

4.2数据结构描述

1. 二维数组`graph`：用来表示图的邻接矩阵。矩阵元素表示两个节点之间的边的权重。如果元素的值为-1，表示两个节点之间没有连接。

2. 一维数组`visited`：用来标记节点是否被访问过。初始时，所有节点都未被访问。

3. 一维数组`path`：用来保存当前路径中的节点。用于记录已经访问的节点和当前路径的权重和。

4. 变量`minWeight`和`minPath`：分别用于保存最小路径的权重和最小路径。

5. 变量`totalWeight`：用于计算每条路径的权重和。

这些数据结构用于存储和处理图的相关信息，以便执行深度优先搜索算法并找到最优路径和权重。

4.3算法描述

算法名称：深度优先搜索

输入：带权邻接矩阵

输出：最短路径以及最短路径之和

定义函数 dfs(node, depth) :

将节点 node 标记为已访问

将节点 node 添加到路径 path 的末尾

If: depth == NUM_NODES - 1：  // 到达叶子节点

    将 totalWeight 设置为0

    对于 i 从 0 到 NUM_NODES - 2：

     If: graph[path[i]][path[i + 1]] == -1：

     将 totalWeight 设置为无穷大  // 不连通的路径

    跳出循环

    totalWeight += graph[path[i]][path[i + 1]]

If:： totalWeight < minWeight：

     将 minWeight 设置为 totalWeight

     将 path 复制到 minPath

否则：

    对于 i 从 0 到 NUM_NODES - 1：

     If: 节点 i 未被访问 并且 graph[node][i] != 0：

     调用 dfs(i, depth + 1)

     将节点 node 标记为未访问  

4.4时间空间复杂度分析

基本运算：比较

递归公式：T(n) = (n-1) * T(n-1)

时间复杂度为：O(n！),时间复杂度比较高，不适合计算大量数据。

空间复杂度：O(n)

4.5算法实例

输入数据：

输出数据：

根据最优路径和为11km，快递员行驶速度为10km/h即1km/6min，在一个小区的投放时间为10分钟，计算得最少时间为146分钟。

5.问题五

你还可以提出什么问题？如何解决该问题？

5.1提出问题

如果需要选择一个地点作为快递枢纽，可以选择在哪？

5.2解决问题

Floyd-Warshall算法是一种动态规划算法，用于计算给定加权图中所有顶点对之间的最短路径。通过该算法，可以找到从每个顶点到其他所有顶点的最短路径，从而确定快递枢纽的位置。

具体步骤如下：

1. 初始化：将所有顶点之间的距离设置为图中给定的权值。
2. 迭代：对于每个顶点k，重新计算所有顶点对(i, j)之间的距离。通过比较经过顶点k和不经过顶点k的路径，更新最短路径。
3. 终止：当所有顶点对之间的距离都稳定时，算法结束。

最终，Floyd-Warshall算法将返回一个距离矩阵，其中每个元素[i][j]表示从顶点i到顶点j的最短路径长度。选择距离之和最小的顶点作为快递枢纽的理想位置。

源码

需要源码的朋友私信作者