代码随想录算法学习心得 15 | 110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和...
一、平衡二叉树
链接:力扣
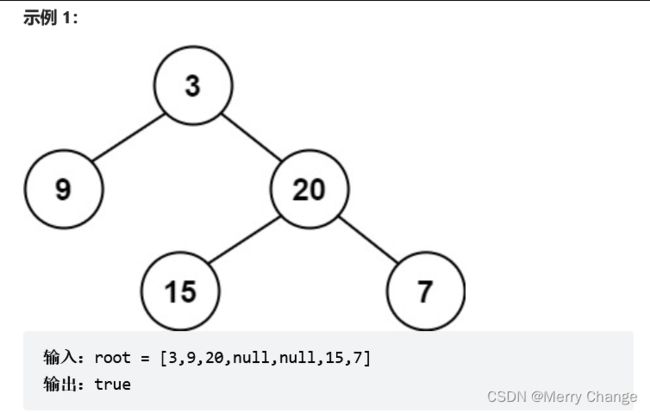
描述:给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
思路:
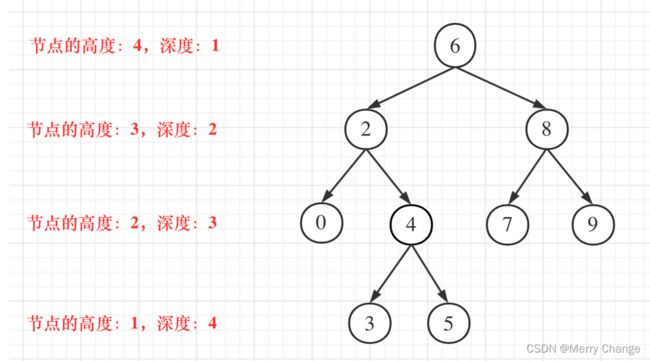
先注意二叉树的深度和高度的概念:
用后序遍历,因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这棵树的最大深度,所以才可以使用后序遍历。 先求出来左子树和右子树的高度,再判断是否是平衡二叉树。
代码如下:
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
int calcheight(TreeNode* node)
{
if (!node)
{
return 0;
}
int leftheight = calcheight(node->left);
int rightheight = calcheight(node->right);
return max(leftheight,rightheight) + 1;
}
bool isBalanced(TreeNode* root)
{
if (!root)
return true;
bool left = isBalanced(root->left);
bool right = isBalanced(root->right);
int l = this->calcheight(root->left);
int r = this->calcheight(root->right);
if (abs(l - r) > 1)
{
return false;
}
return left && right;
}
};
int main()
{
TreeNode* node5 = new TreeNode(4);
TreeNode* node6 = new TreeNode(4);
TreeNode* node3 = new TreeNode(3, node5, node6);
TreeNode* node4 = new TreeNode(3);
TreeNode* node1 = new TreeNode(2, node3, node4);
TreeNode* node2 = new TreeNode(2);
TreeNode* root = new TreeNode(1,node1,node2);
Solution s;
int ret1=s.calcheight(root->left);
int ret2=s.calcheight(root->right);
cout << boolalpha << s.isBalanced(root) << endl;
return 0;
} 运行如下:
二、二叉树的所有路径
链接:力扣
描述:给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
思路如下:
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。在这道题目中第一次涉及到回溯,要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
递归三部曲:
1、递归函数参数以及返回值
要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值。
2、确定递归终止条件
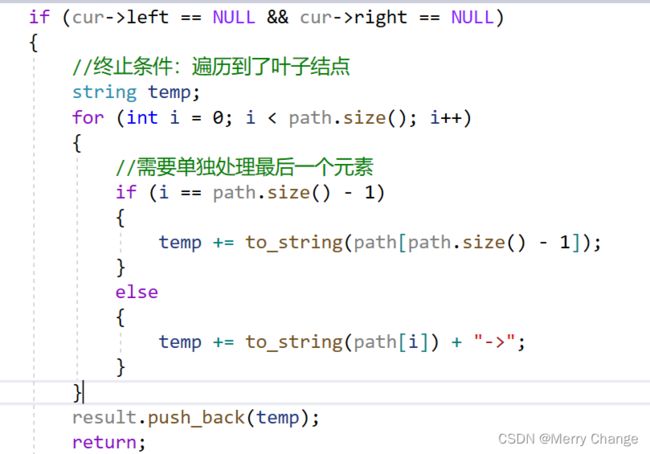
但是本题的终止条件这样写会很麻烦,因为本题要找到叶子节点,就开始结束的处理逻辑了(把路径放进result里)。我们需要找到叶子结点
那么什么时候算是找到了叶子节点? 是当 cur不为空,其左右孩子都为空的时候,就找到叶子节点。
3、确定单层逻辑
注意:
1、回溯和递归是一一对应的,有一个递归,就要有一个回溯所以回溯要和递归永远在一起,世界上最遥远的距离是你在花括号里,而我在花括号外!
2、如果vector
代码如下:
#include
#include
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution {
public:
void func(TreeNode* cur,vectorpath,vector&result)
{
//前序遍历
path.push_back(cur->val);
if (cur->left == NULL && cur->right == NULL)
{
//终止条件:遍历到了叶子结点
string temp;
for (int i = 0; i < path.size(); i++)
{
//需要单独处理最后一个元素
if (i == path.size() - 1)
{
temp += to_string(path[path.size() - 1]);
}
else
{
temp += to_string(path[i]) + "->";
}
}
result.push_back(temp);
return;
}
//单层逻辑
if (cur->left)
{
//左子树
func(cur->left, path, result);
}
if (cur->right)
{
func(cur->right, path, result);
}
}
vector binaryTreePaths(TreeNode* root)
{
vectorresult;
if (!root)
{
return result;
}
vectorpath;
this->func(root, path, result);
return result;
}
};
int main()
{
TreeNode* node3 = new TreeNode(5);
TreeNode* node1 = new TreeNode(2, NULL, node3);
TreeNode* node2 = new TreeNode(3);
TreeNode* root = new TreeNode(1, node1, node2);
Solution s;
s.binaryTreePaths(root);
return 0;
} 运行如下:
三、左叶子之和
链接:力扣
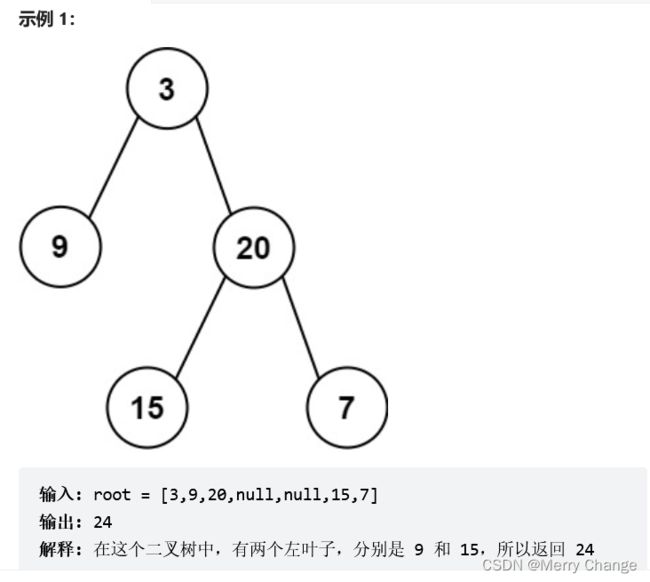
描述:给定二叉树的根节点 root ,返回所有左叶子之和。
思路如下:
层序遍历是行不通的,只能判断是不是叶子节点,无法判断是不是左叶子结点。叶子节点的定义为:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点。
判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子。
代码如下:
#include
#include
#include
#include
using namespace std;
struct TreeNode
{
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution
{
public:
void func(TreeNode *cur,int &num)
{
if (!cur)
{
return;
}
if (cur->left && cur->left->left == NULL && cur->left->right == NULL)
{
num += cur->left->val;
}
int left = sumOfLeftLeaves(cur->left);
int right = sumOfLeftLeaves(cur->right);
num += left + right;
}
int sumOfLeftLeaves(TreeNode* root)
{
//前序遍历
int num = 0;
this->func(root, num);
return num;
}
};
int main()
{
TreeNode* node3 = new TreeNode(15);
TreeNode* node4 = new TreeNode(7);
TreeNode* node1 = new TreeNode(9, NULL, NULL);
TreeNode* node2 = new TreeNode(20,node3,node4);
TreeNode* root = new TreeNode(3, node1, node2);
Solution s;
s.sumOfLeftLeaves(root);
return 0;
} 运行如下: