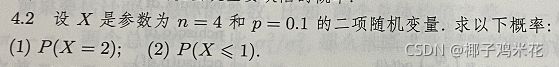2021-10-14 统计学-基于R（第四版）第四章课后习题记录及总结

这章作业基本上就是套用课本的公式，没什么特别，这篇博客就是一个记录。

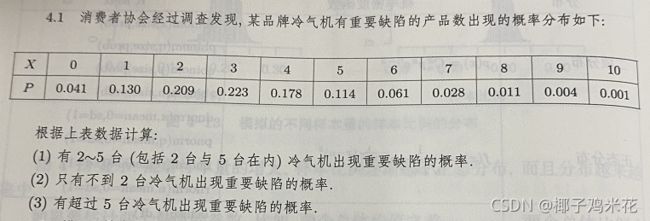
4.1

> exer1<-read.csv("D:/作业/统计学R/《统计学—基于R》（第4版）—例题和习题数据（公开资源）/exercise/chap04/exercise4_1.csv")
（1）
> sum(exer1$P[3:6])  #2~5台出现缺陷概率
[1]0.724
（2）
> sum(exer1$P[1:2])  #不到2台出现缺陷概率
[1]0.171
（3）
> sum(exer1$P[7:11])  #超过5台出现缺陷概率
[1]0.105

---

4.2

（1）
> dbinom(2,4,0.1)  #P(X=2)
[1]0.0486
（2）
> pbinom(1,4,0.1)  #P(X<=1)
[1]0.9477

---

4.3

（1）
> 1-pnorm(510,mean=500,sd=20)  #P(X>=510)
[1] 0.3085375
> pnorm(450,mean=500,sd=20)-pnorm(400,mean=500,sd=20)  #P(400<=X<=450)
[1] 0.006209379
（2）
> pnorm(1.2,mean=0,sd=1)-pnorm(0,mean=0,sd=1)  #P(0<=Z<=1.2)
[1] 0.3849303
> pnorm(0,mean=0,sd=1)-pnorm(-0.48,mean=0,sd=1)  #P(-0.48<=Z<=0)
[1] 0.1843863
> 1-pnorm(1.2,mean=0,sd=1)  #P(Z>=1.2)
[1]0.1150697
（3）
> qnorm(0.95,mean=0,sd=1)  #累积概率为0.95时的反函数值
[1]1.644854

---

4.4

（1）
> pt(-1.5,df=15)  #df=15,t<-1.5
[1] 0.07718333
> 1-pt(2,df=20)  #df=20,t>2
[1] 0.02963277
> qt(0.95,df=30)  #df=30,t分布右尾概率为0.05时的t
[1]1.697261
（2）
> pchisq(12,df=8)  #df=8,卡方<12
[1] 0.8487961
> 1-pchisq(18,df=20)  #df=20,卡方>18
[1] 0.5874082
> qchisq(0.975,df=15)  #卡方分布右尾概率为0.025时的反函数值
[1]27.48839
（3）
> pf(3.5,df1=15,df2=10)  #df1=15,df2=10,F<3.5
[1]0.9744715
> 1-pf(3,df1=12,df2=8)  #df1=12,df2=8,F>3
[1]0.06353421
> qf(0.975,df1=20,df2=16)  #F分布右尾概率为0.025时的F值
[1] 2.680793

4.5懒得搞了，就酱紫吧~