神经网络辨识器的作用,神经网络图像识别技术
液压泵 恒流问题
。
迄今为止,国内外有2种实现泵恒流量调节的方法:一种是在泵的主油路上设置一流量敏感装置,将流量信号转换为压差、位移、力或电压信号,再将其与给定信号比较实现流量反馈调节,达到泵恒流量输出;另一种是采用泄漏电补偿方法,通过检测泵的负载压力、油温等参数由补偿数学模型间接辨识出泵的实际输出流量误差,并对泵的给定信号进行电补偿修正,以达到使泵的输出流量恒定。
这2种方法均能较为满意地实现泵恒流量控制。但是,前者因在主油路上直接检测负载流量,不可避免地带来了附加的节流功率损失;后者由于须先通过实验确定补偿数学模型中的变量系数,建模工作变得繁琐。
同时由于模型是近似线性的,因而精度也受到一定影响。液压泵流量调节系统因受流量—压力特性、滞环特性、死区特性以及粘温特性、质量惯性等的影响,是典型的非线性和时变系统〔1〕。
运用传统的经典控制方法控制液压泵流量调节系统,难以获得满意的控制效果,特别是在工程应用中,当工况发生较大变化使调节系统参数发生较大变化时,会使系统的控制性能明显下降,甚至不能满足工程要求〔2〕。
笔者在分析液压泵恒流量调节方式和特点的基础上,提出一种采用神经网络辨识负载流量原理实现液压泵恒流量调节的新方法。
结合此方法,提出一种基于模糊神经网络的智能学习控制方法,并将其应用于电液比例恒流量调节轴向柱塞泵的控制。
1 基于负载流量神经网络模型的液压恒流泵原理液压泵输出的负载流量实际上是由泵的排量、负载压力、流体介质粘度、泵轴转速等变量决定的复杂的非线性多元函数,很难用精确的数学模型表示。
神经网络因其自身的结构特点,具有逼近任何非线性函数的能力、对复杂不确定系统自学习能力和高度的并行运算能力〔3〕。
因此,可以利用神经网络的特性建立负载流量的神经网络模型并将此模型作为负载流量辨识器引入液压泵流量调节系统中,通过检测各变量间接辨识出泵的实际输出流量,再将其与给定信号比较,实现流量反馈调节,达到恒流量输出。
其原理见图1。这里,用做负载流量辨识器的神经网络须经学习训练得到。我们采用3层前馈神经网络。
由于流体介质粘度主要受温度和压力影响,且泵轴转速变化对负载流量影响相对较小,所以我们从工程应用角度出发,选取泵的负载压力、排量、液体温度作为网络的输入,泵的负载流量作为网络的输出,并采取归一化处理。
隐层和输出层的激励函数取为Sigmoid函数式中,neti为第i个神经元的输入;θi为阈值。训练网络的指标函数定义为式中,Yp为第p个学习样本;Op为相应的网络实际输出;n为训练样本数。
采用最速下降法调整输入层和隐层、隐层和输出层之间的权重、使E达到最小,即第k次迭代的权重修正为式中,l=1,2;β为学习率,β∈(0,1);α为惯性系数。
通过调整、以及θi,可实现对负载流量的建模估计。
从现场采集来的数据通常都会存在各种干扰噪声,为了最大限度地避免这些噪声对网络建模的干扰,我们在利用神经网络学习建模时,采用了一种分组训练检验的方法,即将获得的样本数据分成两组,一组数据用来训练网络,而另一组数据用来评价网络的映射学习结果。
网络误差的评估公式定义为式中,m为测试样本数;Yj为第j个测试样本;Oj为相应的网络实际输出。实验证明该方法对提高建模精度是有效的。
由于负载流量与各变量的非线性函数关系可以通过调整神经网络的权重和阈值得到,因此避免了采用最小二乘多项式拟合方法建立流量补偿数学模型时,必须由实验确定各自变量系数所带来的麻烦。
而且,这种基于负载流量神经网络模型的恒流泵也避免了传统的恒流泵因在主油路上直接检测负载流量所带来的附加的节流功率损失。从理论上讲,以零功率损失实现了液压泵的恒流量调节。
图1 基于负载流量神经网络模型的液压恒流泵原理2 基于模糊神经网络的恒流泵智能学习控制根据液压泵流量调节系统具有时变和非线性的特点,结合上面提出的这种采用神经网络辨识负载流量原理实现液压泵恒流量调节的新方法,我们设计了基于模糊神经网络的恒流泵智能学习控制系统,其结构原理见图2。
控制器由模糊神经网络控制器和定增益线性控制器复合构成。模糊神经网络FNN控制器采取常用的二维输入一维输出结构。
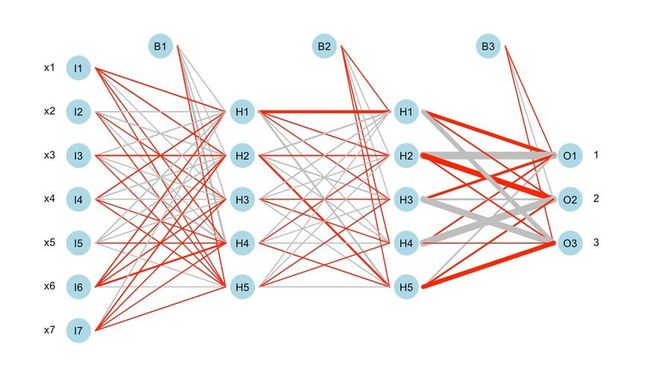
网络的Ⅰ层、Ⅱ层对应于模糊规则的前件,隶属函数取高斯基函数f()=exp〔-(xk-aik)2/〕(i=1,…,7,k=1,2);Ⅲ层、Ⅳ层对应规则后件。
网络的输入端分别对应流量理想设定和负载压力,这样会使模糊神经网络能在理想的流量轨迹附近学习,并能实现系统状态的动态补偿。
定增益线性控制器作为系统反馈控制器可以避免神经网络控制初始误差,并提供神经网络学习信号,起控制器与学习机制双重作用。
这里引入智能调节器的目的是对系统运行状态进行评价,根据偏差及其变化情况在线调整定增益线性控制器(PID控制器)的参数和学习算法中的学习因子。
智能调节器由一系列产生式规则组成,它的建立基于如下几条规则:①若偏差及其变化很小,则比例、积分、微分作用减弱;②偏差为正时,若偏差较小,则比例、积分作用增强,微分作用减弱;③偏差为负时,若偏差较大,则积分、微分作用减弱;④若偏差增加,则学习因子减小,反之,则学习因子增大。
其中,规则①比例、积分、微分作用减弱是为了保持控制提高控制精度;规则②比例、积分作用增强和微分作用减弱是为了减小静差提高控制精度;规则③减弱积分、微分作用是为了兼顾稳定性与调节精度;规则④是为了提高算法的稳定性和收敛速度。
总结以上规则和分析,给出系统的控制算法如下:调节器:if(|e(t)|<e1∩|c(t)|<c1)then(k1=α1,k2=β1,k3=γ1)if(e(t)>0∩e(t)<e2)then(k1=α2,k2=β2,k′3=γ2)if(e(t)<0∩e(t)<-e3)then(k1=α3,k2=β3,k3=γ3)if(e(t)c(t)<0)then(ψ=λ1)if(e(t)c(t)>0)then(ψ=λ2)else(k1=1,k2=1,k3=1,ψ=1)控制器:PID控制器u1(t)=u1(t-1)+k1kp(e(t)-e(t-1))+k2kie(t)+K3kd(e(t)-2e(t-1)-e(t-2))FNN控制器这里e(t)=Q*(t)-Q(t)=Q*(t)-�φ(p(t),q