【光波电子学】基于MATLAB的多模光纤模场分布的仿真分析
基于MATLAB的多模光纤模场分布的仿真分析
一、引言
(1)多模光纤的概念
多模光纤(MMF)是一种具有较大纤芯直径的光纤结构,其核心直径通常在10-50微米范围内。与单模光纤(SMF)相比,多模光纤可以容纳多个光信号模式传播,因此在许多应用中具有广泛的用途。
多模光纤的工作原理基于多个光模式在纤芯中的传播。每个光模式可以看作是一个光束,具有自己的传播方向和相位。在传输过程中,这些模式会互相干涉,导致在光纤尾部出现光场分布的变化。多模光纤主要由纤芯、包层和护层组成。纤芯用于传输光信号,而包层则用于限制光信号的传播范围,并减小光信号的损耗。
多模光纤的优点是可以传输大量的光信号,适用于需要高通量和高带宽的应用。此外,由于纤芯直径较大,制造成本相对较低。多模光纤也可以与其他光学器件(如光学耦合器和分束器)结合使用,进一步扩展其应用领域。然而,多模光纤的缺点是存在多个模式的干涉和色散问题。这会导致信号失真和传输速率的降低,在一些对信号质量要求较高的应用中可能限制了其使用。
(2)实现多模光纤的方法及优缺点
实现多模光纤的方法主要包括两种:径向抽运和溅射法。
径向抽运是一种常用的方法,通过使用高能激光束沿纤芯径向照射的方式,来改变纤芯的折射率分布。从而形成多个模式的分布。这种方法简单易行,可以在现有光纤基础上进行改造,只需通过特定的激光参数进行调节即可得到所需的多模光纤结构。但是,这种方法存在光强不均匀的问题,可能导致光信号的耦合效率下降。
溅射法是另一种常用的方法,它通过将带有特殊结构的材料溅射在纤芯表面来实现多模光纤的制造。这种方法可以灵活调节纤芯的形状和尺寸,从而得到更好的纤芯折射率分布。这种方法的优点是制备过程较为简单,可以获得较为均匀的多模分布。然而,溅射法的缺点是制备过程较为复杂,需要使用特殊的设备和工艺,并且制备成本相对较高。
(3)仿真多模光纤模场分布方法及优缺点
多模光纤模场分布仿真的常用方法分为基于有限元法的分析方法、基于模式耦合方程的分析方法、基于光线追迹法的分析方法。首先,基于有限元法的分析方法能处理各种光纤结构,得到高精度的结果,但算法复杂,计算耗时长。其次,基于模式耦合方程的分析方法凭借其精确性和强大的理论基础,适用于各种光纤结构,但数值求解较复杂。最后,基于光线追迹法的分析方法简单且计算速度快,适用于简单光纤结构,但处理复杂光学现象能力有限。因此,在选择仿真方法时需综合考虑光纤结构、精度需求和计算资源等因素。对于精度要求较高且计算资源充足的情况,可以采用有限元法或模式耦合方程方法;而在时间和计算资源有限的情况下,可选择光线追迹法作为快速的近似方法。总之,在仿真多模光纤模场分布问题中,不同的方法各有优劣,需要根据具体情况选择合适的方法以达到较准确的结果。
本实验将采用基于模式耦合方程的分析方法。在弱导近似下,可以利用模式耦合方程来分析由 H E l + 1 , m HE_{l+1,m} HEl+1,m模和 E H l − 1 , m EH_{l-1,m} EHl−1,m模组合的模式,进而得到线性偏振模式 L P l m LP_{lm} LPlm。模式耦合方程方法适用于光纤中光模式的耦合和传输过程,能够较准确地描述复杂的光场分布情况,因此适合用于分析这种模式的组合。
二、理论基础
2.1 多模光纤模式
在多模光纤中,光可以以多种不同的模式传播,每种模式对应着不同的空间分布和频率。多模光纤中的模式可以通过横向电场分布和纵向电场分布来描述。对于多模光纤,一般将其横截面划分成许多模式场,每个模式都对应着一个特定的传输方式和特征模场分布。设直径为d的多模光纤,其模式可以用以下数学公式表示:
V = 2 π n a λ n 1 2 − n 2 2 V = \frac{{2 \pi n a}}{\lambda} \sqrt{n_1^2 - n_2^2} V=λ2πnan12−n22
其中,V是光的归一化频率参数,n是光纤的折射率,a是光纤的半径,λ是光的波长,n1和n2分别是光纤的内层和外层折射率。
2.2 模场分布的描述
光纤中的模式分布是指光场在空间中的分布特性,在多模光纤中,模式分布描述了光场的横向和纵向分布特性,可以通过横向和纵向电场分布函数来表示模式的光场分布。
横向电场分布描述了光纤中横向方向上的电场强度分布特性,一般可用Hermite-Gaussian函数或Laguerre-Gaussian函数数学公式来表示。Hermite-Gaussian 函数是描述横向模式的一类基函数,而 Laguerre-Gaussian 函数则广泛用于描述更复杂的模式,例如旋转和角动量。这些函数是解波动方程后得到的特定形式的解,可以描述不同类型的模式在横向方向上的分布特性。
纵向电场分布描述了光场沿光纤轴向的分布特性,可用传输矩阵法等数学方法求解得到。光场的纵向分布特性对于光纤的传输和耦合等性能具有重要影响,因此对其进行准确的描述和仿真分析至关重要。
光场分布的描述可以帮助理解光在多模光纤中的传输特性,包括光的衍射、色散、耦合损耗等现象。通过数学模型和仿真分析,可以得到光场在光纤中的传输特性。
(1)Hermite-Gaussian 函数
Hermite-Gaussian 函数描述的是横向电场分布,它可以用于多模光纤中的光波的横向模式。Hermite-Gaussian 函数可以表示为:
H m n ( x , y ) = 1 σ x σ y H m ( 2 x σ x ) H n ( 2 y σ y ) e − x 2 σ x 2 e − y 2 σ y 2 H_{mn}(x, y) = \frac{1}{\sigma_x \sigma_y} H_m(\frac{\sqrt{2}x}{\sigma_x}) H_n(\frac{\sqrt{2}y}{\sigma_y}) e^{-\frac{x^2}{\sigma_x^2}} e^{-\frac{y^2}{\sigma_y^2}} Hmn(x,y)=σxσy1Hm(σx2x)Hn(σy2y)e−σx2x2e−σy2y2
其中, H m H_m Hm 和 H n H_n Hn是 Hermite 多项式, σ x \sigma_x σx 和 σ y \sigma_y σy是横向方向的标准偏差。 H m n ( x , y ) H_{mn}(x, y) Hmn(x,y) 描述了光波在横向空间的电场分布,其中的 m 和n 是与模式密切相关的整数指数。
(2)Laguerre-Gaussian 函数
Laguerre-Gaussian 函数描述的是光波的纵向电场分布,它包含了更丰富和复杂的模式信息。Laguerre-Gaussian 函数可以表示为:
L G p , l ( r , θ , z ) = A ( 2 π r w ( z ) ) ∣ l ∣ L p ∣ l ∣ ( 2 r 2 w 2 ( z ) ) e − r 2 w 2 ( z ) e − i k z e i l θ LG_{p,l}(r, \theta, z) = A \left( \sqrt{\frac{2}{\pi}} \frac{r}{w(z)} \right)^{|l|} L_p^{|l|}\left( \frac{2r^2}{w^2(z)} \right) e^{-\frac{r^2}{w^2(z)}} e^{-ikz} e^{il\theta} LGp,l(r,θ,z)=A(π2w(z)r)∣l∣Lp∣l∣(w2(z)2r2)e−w2(z)r2e−ikzeilθ
其中,A是归一化系数, w(z) 是 Gauss 横向束腰半径, L p ∣ l ∣ L_p^{|l|} Lp∣l∣是以 L p L_p Lp表示的关联 Laguerre 多项式,r 和 θ \theta θ分别是极坐标下的径向距离和角度,z是传输距离,k是波矢,而 l 和p是与光波的角动量和径向指数相关的整数。
Laguerre-Gaussian 函数能够描述光波在光纤中的传播行为、角动量以及形成复杂模式的能力。这种函数是为了解决高斯光束的纵向传输而引入的,可在光纤的输出端获得与其横向电场分布相关的模式信息。
三、MATLAB仿真模型设计
% 参数设置
a = 25e-6; % 光纤核径 (25微米)
lambda = 1550e-9; % 光波长 (1550 nm)
n_core = 1.45; % 核心折射率
n_cladding = 1.44; % 包层折射率
V = 2.405; % V参数, 通常由 a, lambda 和 n_core, n_cladding确定
delta = (n_core^2 - n_cladding^2)/(2*n_core^2); % 相对折射率差
% 选定模式对应的 l 和 m
l = 1;
m = 1;
% Hermite-Gaussian函数参数
M = 1; % Hermite-Gaussian x方向模式数
N = 1; % Hermite-Gaussian y方向模式数
% 网格设置
r_max = 5*a; % 设置画图半径为光纤核半径的5倍
points = 200; % 分辨率
[x, y] = meshgrid(linspace(-r_max, r_max, points), linspace(-r_max, r_max, points));
r = sqrt(x.^2 + y.^2);
phi = atan2(y,x);
% HE和EH模式的振幅系数
A_he = V * sqrt(2/(pi * factorial(l) * 2^l)) * (sqrt(2) * r/a).^l ...
.* exp(-r.^2/a^2) .* cos(l * phi);
A_eh = V * sqrt(2/(pi * factorial(l) * 2^(l-2))) * (sqrt(2) * r/a).^(l-2) ...
.* exp(-r.^2/a^2) .* cos((l-2) * phi);
% LP模式的横向电场分布 (HE, EH模式的线性组合)
E_transverse = A_he + A_eh;
% 采用传输矩阵法求解纵向电场分布
k0 = 2 * pi / lambda; % 自由空间波数
gamma = sqrt(n_core^2*k0^2 - (l*pi/(2*a))^2 - (m*pi/(2*a))^2); % 衰减常数
z = linspace(0, 10e-3, 500); % z方向网格
E_longitudinal = exp(-1i*gamma*z); % 纵向电场分布
% 横向电场分布的可视化
figure(1);
imagesc(linspace(-r_max, r_max, points)*1e6, linspace(-r_max, r_max, points)*1e6, abs(E_transverse).^2);
axis square;
xlabel('x (μm)');
ylabel('y (μm)');
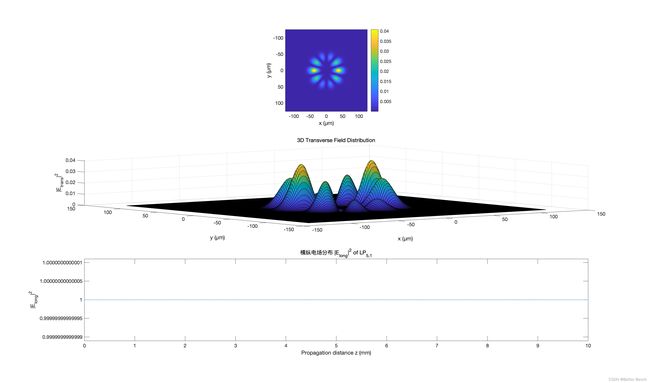
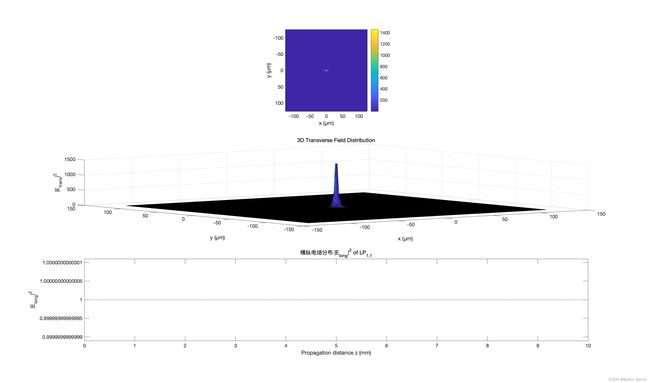
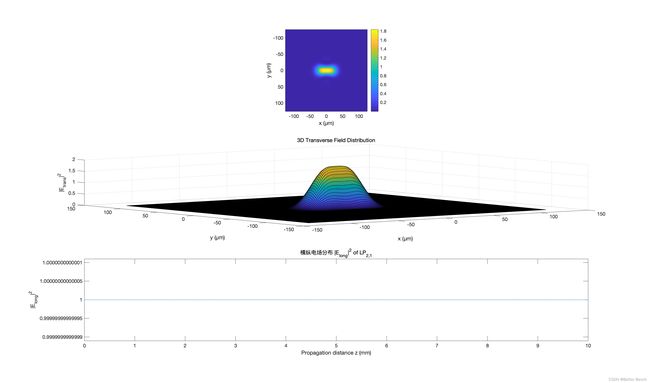
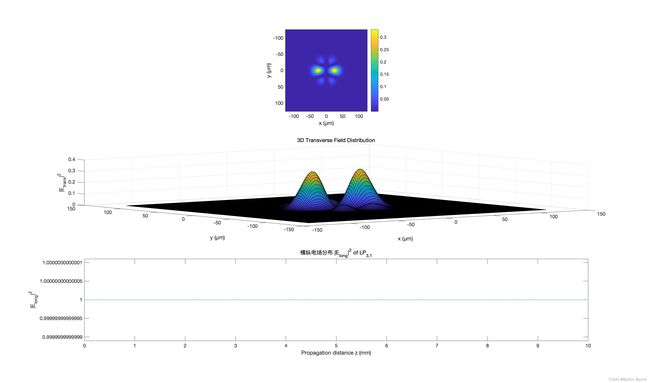
title('横向电场分布 |E_{trans}|^2 of LP_{1,1}');
colorbar;
% 纵向电场分布的可视化
figure(2);
plot(z*1e3, abs(E_longitudinal).^2);
xlabel('Propagation distance z (mm)');
ylabel('|E_{long}|^2');
title('纵向电场分布 |E_{long}|^2 of LP_{1,1} ');
四、仿真结果分析
4.1 不同模式的光场分布
在仿真中可以观察到不同模式的光场分布。其中,代码中通过修改变量l,可以选择不同的模式数,对应于不同的径向模式。然后,通过使用Hermite-Gaussian函数和选择的模式数,计算对应的横向电场分布。最后,通过传输矩阵法求解纵向电场分布。对于给定的光纤参数,通过修改l参数,可以选择不同的模式。结果中的图像展示了横向和纵向电场的分布情况。横向电场分布显示在上方的图像,图像的坐标轴表示在光纤横向平面内的位置。纵向电场分布显示在下方的图像,图像的横坐标表示传播距离,纵坐标表示电场的强度。通过观察这些图像,可以清晰地看到不同模式之间的差异。对于较低的模式数,光场分布呈现出类似高斯光束的形状,即光束在光纤径向上的分布类似高斯分布。而对于较高的模式数,光场分布呈现出更多的波峰和波谷,形成一种更复杂的结构。
4.2 参数对模场分布的影响
光场分布受到光纤参数的影响。在给定的代码中,可以通过修改光纤的核径、光波长、核心折射率和包层折射率来改变光纤的参数。在这些参数的不同取值下,仿真可以得出不同的光场分布情况。例如,核径的变化会导致光场分布的形状和尺寸的变化。较大的核径会导致光场分布的尺寸扩大,而较小的核径则会使其更加集中。此外,光波长的变化也会对光场分布产生影响。较短的光波长会导致光场分布的精细结构变得更加明显,而较长的光波长则会使其变得模糊一些。光纤的核心折射率和包层折射率对模场分布也有重要影响。它们之间的差异决定了相对折射率差的值。较大的相对折射率差会导致光场在光纤中的传播受到更明显的限制,形成更复杂的光场分布。通过对这些参数的改变,可以进一步理解光场在光纤中的传播行为,并优化光纤设计以满足不同应用需求。