损失函数介绍

目录

损失函数

平均绝对误差

均方误差

交叉熵损失

反向传播

实战环节

---

损失函数

        损失函数（Loss Function）是一种用于衡量模型预测值与真实值之间差异的函数。在机器学习中，通常使用损失函数来评估模型的性能，并通过最小化损失函数来调整模型的参数，损失值越小，表示模型的预测结果与真实值越接近。简单来说可以总结为两点：

• 计算实际输出和目标之间的差距
• 为更新输出提供一定的依据

注：本部分只是对常用损失函数的使用方法及理论进行简单说明，若要具体了解其背后实现原理，请自行查阅，详尽信息可参考官方文档：损失函数

平均绝对误差

平均绝对误差（Mean Absolute Error，MAE）是一种回归问题的常见评估指标，用于衡量预测值与真实值之间的平均绝对差异程度。

计算平均绝对误差的步骤如下：

• 对于每个样本，计算预测值与真实值之间的绝对差值
• 将所有样本的绝对差值求和
• 将总和除以样本数量，得到平均绝对误差

数学公式表示为： MAE = (1/n) * Σ|y_pred - y_true|

其中，n 表示样本数量，y_pred 表示预测值，y_true 表示真实值。

示例如下：X 为输入，Y 为输出，MAE=0.6

均方误差

均方误差（Mean Squared Error，MSE）是回归任务中广泛使用的损失函数，它计算模型预测值与真实值之间的平均二次误差。

计算均方误差的步骤如下：

• 对于每个样本，计算预测值与真实值之间的差值的平方
• 将所有样本的平方差值求和
• 将总和除以样本数量，得到均方误差

数学公式表示为： MSE = (1/n) * Σ(y_pred - y_true)^2

其中，n 表示样本数量，y_pred 表示预测值，y_true 表示真实值。示例如下：

交叉熵损失

交叉熵损失（CrossEntropy Loss）是分类任务中常用的损失函数，通过将预测结果的概率分布与真实标签的概率分布进行比较，来计算模型的损失。

个人理解，仅供参考：实际上，每一种类别都有两个概率，实际概率 p 和预测概率 q，在原始数据集中，通常需要手动标注或者提供真实的标签信息，这些标签可以转化为实际的概率分布，其中一个类别的概率为1，其余类别的概率为0（或者使用one-hot编码表示），而预测概率是经过神经网络分类后得到的概率，那么它们之间的交叉熵为：H(p,q) = -Σ(p(x) * log(q(x)))。当我们用分布 q 来拟合分布 p 时，每匹配一个元素，就会产生一个损失，交叉熵就是所有损失的总和。如果 p 和 q 相同，那么交叉熵等于 p 的熵，即：H(p,p) = -Σ(p(x) * log(p(x)))。交叉熵的值越小，表示两个概率分布越接近，也就是说模型的预测结果与真实标签越接近。

注：以上只是一个简单说明，表述可能并不清晰，若有误解，请谅解！详细请查看官方说明。

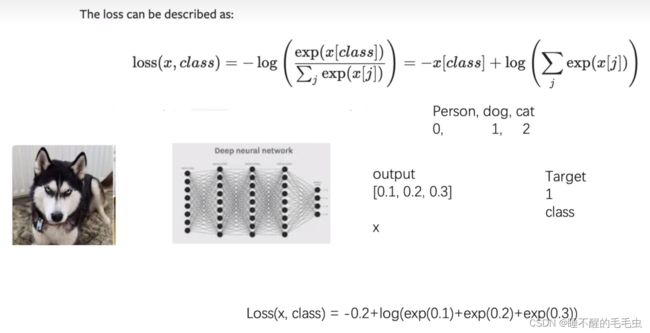
这里通过一个例子来进行补充：交叉熵的计算公式如下图示：其中 X 表示输入数据中各类型的概率而构成的列表，class 是目标类别，交叉熵值=目标类别概率的负数 + 各概率的对数和

假设有 Person，dog，cat 三种类别构成的数据集，经过神经网络后得到对应的概率分别为 0.1，0.2，0.3，而目标类别是dog，我们将对应类别概率经过计算就会得到交叉熵，当 target 取到正确的类别后会得到最小的交叉熵，此时表示模型的预测效果最好。

反向传播

反向传播（Backpropagation）是一种基于梯度的优化算法，用于计算损失函数对于模型参数的梯度，并根据梯度更新模型的参数，可以理解为负反馈机制。

反向传播的过程可以分为以下几个步骤：

• 前向传播（Forward Propagation）：将输入数据通过神经网络的各层进行前向传播，得到模型的预测值

• 损失计算（Loss Calculation）：将模型预测值与真实值进行比较，使用选择的损失函数计算出损失值

• 反向传播（Backpropagation）：从损失函数开始，根据链式法则计算损失函数对于模型参数的梯度。反向传播从输出层开始，逐层计算每个参数的梯度，然后将梯度传递回网络的每一层

• 参数更新（Parameter Update）：根据梯度下降法则，使用损失函数对于模型参数的梯度，更新模型的参数。通常使用优化算法（如随机梯度下降）来更新参数，以使损失函数逐步减小

• 重复迭代：重复执行前向传播、损失计算、反向传播和参数更新的过程，直到达到停止条件（如达到最大迭代次数或损失函数收敛）

通过不断迭代上述步骤，神经网络能够逐渐调整参数，使得模型的预测结果与真实值更加接近，并且最小化损失函数。这样训练出来的模型就能够用于进行预测和分类等任务。

实战环节

本部分的数据均和理论部分一致，可通过运行程序检验上述逻辑是否正确。

MAE相关代码如下：

import torch
from torch import nn

input = torch.tensor([1, 2, 3], dtype= torch.float32)
targets = torch.tensor([1, 2, 5], dtype= torch.float32)
loss = nn.L1Loss()
results = loss(input, targets)
print(results)

MSE相关代码：

import torch
from torch import nn

input = torch.tensor([1, 2, 3], dtype= torch.float32)
targets = torch.tensor([1, 2, 5], dtype= torch.float32)
loss_mse = nn.MSELoss()
result_mse = loss_mse(input, targets)
print(result_mse)

CrossEntropy相关代码：

import torch
from torch import nn

input = torch.tensor([1, 2, 3], dtype= torch.float32)
targets = torch.tensor([1, 2, 5], dtype= torch.float32)
loss_cross = nn.CrossEntropyLoss()
result_cross = loss_cross(input, targets)
print(result_cross)