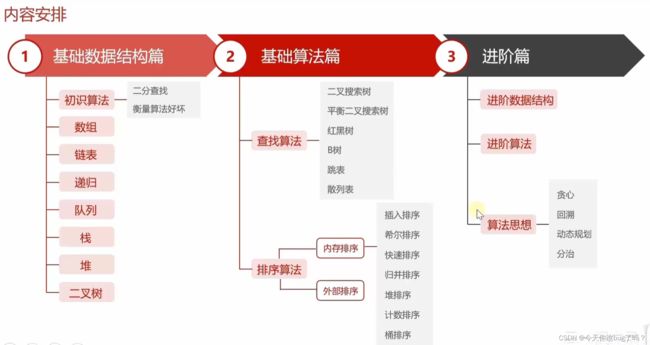
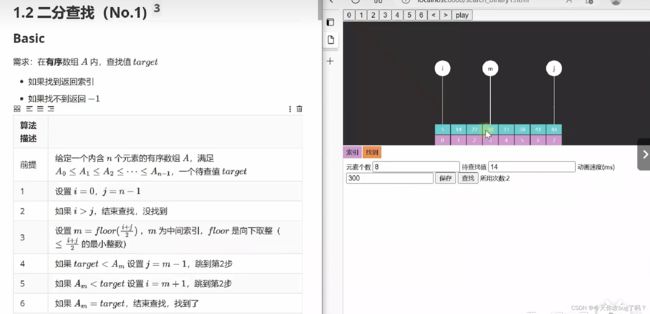
java二分查找
public class BinaarySearch {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length-1;//设置指针和初始值
while (i<=j){
//范围内有东西
// int m=(i+j)/2;
int m=(i+j)>>>1;
if (target改动版:
public class BinaarySearch {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length;//第一处
while (i>>1;
if (target 一、事前分析法
右侧运算次数:
二、衡量算法好坏的标准
2.1 时间复杂度
计算机科学中,时间复杂度是用来衡量:一个算法的执行,随数据规模增大,而增长的时间成本
不依赖于环境因素
如何表示时间复杂度呢?
假设算法要处理的数据规模是n,代码总的执行行数用函数 f(n)来表示,例如:
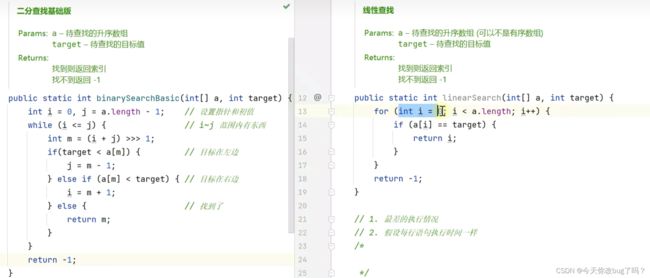
线性查找算法的函数 f()= 3 * n +30
二分查找算法的函数 f(n) = (floor(log2(n)) + 1)* 5 +4
为了对 f(n)进行化简,应当抓住主要矛盾,找到一个变化趋势与之相近的表示法
大O表示法:
其中
- c,c1,c2 都为一个常数
- f(n)是实际执行代码行数与 n 的函数g(n)是经过化简,变化趋势与 f(n)一的 n 的函数
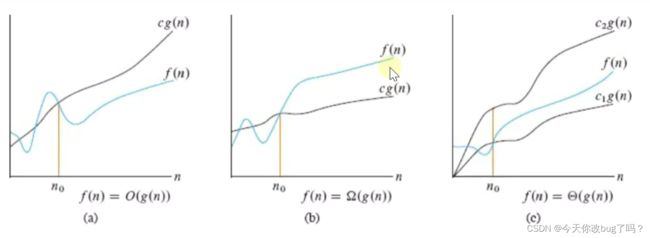
asymptotic upper bound(算法执行的最差的情况)
渐进上界: 从某个常数 n开始,c*g(n) 总是位于 fn) 上方,那么记作 O(g(n))
举例:f(n)= n^2 +100,从n0 = 10 时,g(n)=2*n^2是它渐进上界,记作 O(n^2)
已知f(n)来说,求g(n):
表达式中相乘的常量,可以省略,如
f(n)=100*n^2中的100
多项式中数量规模更小(低次项) 的表达式,如
f(n)=n^2+n中的n
f(n)=n^3+n^2中的n^2
不同底数的对数,渐进上界可以用一个对数函数log n 表示
例如: log2(n)可以替换为 log10(n),因为 log2(n)=log10(n)/log10(2),相乘的常量1/log10(2)可以省略
类似的,对数的常数次幂可省略
如: log(n^c)=c*log(n)
asymptotic lower bound(算法执行的最优的情况)
渐进下界: 从某个常数n0开始,c* g(n) 总是位于 f(n)下方,那么记作Ω (g(n))
asymptotic tight bounds
渐进紧界: 从某个常数n0开始,f(n) 总是在 c1 * g(n)和c2 * g(n)之间,那么记作θ (g(n))
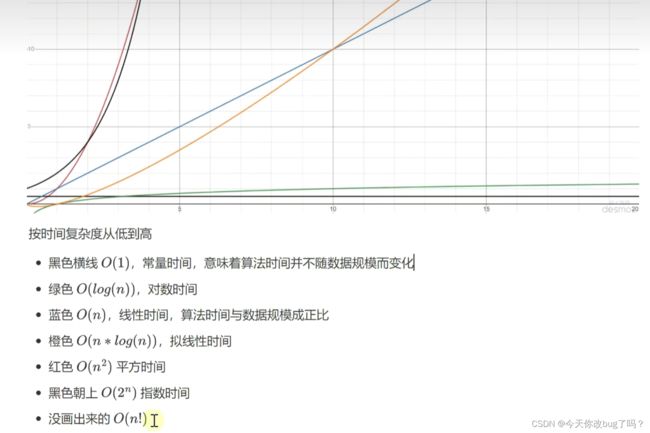
常见大O表示法
2.2 空间复杂度
三、二分查找性能
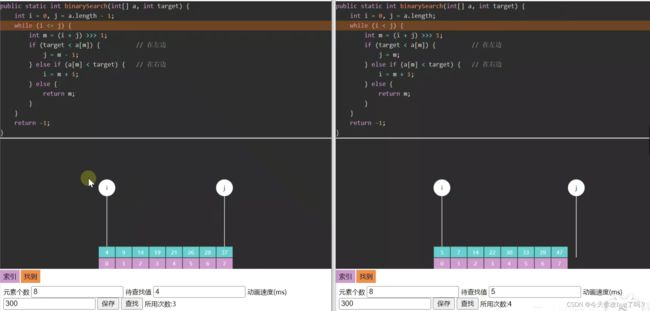
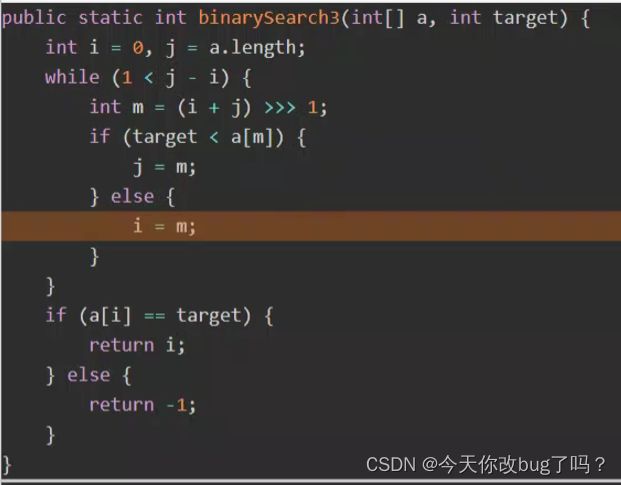
之前的代码中,if-else代码,若目标值在左侧,则需要比较n次;若目标值在右侧,则需要比较2n次。
1.左闭右开的区间,i 指向的可能是目标,而j 指向的不是目标
2.不在循环内找出,等范围内只剩i 时,退出循环,在循环外比较 a[i] 与 target
3.优点:循环内的平均比较次数减少了(之前是if-else比较次数不均衡,现在不是if就是else,比较次数减少也更均衡)
4.缺点:改动前最优结果是O(1),改动后上下界时间复杂度都是θ(log(n))
四、binarySearch()
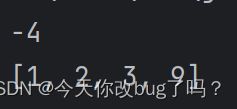
二分查找没找到目标值时,返回值的含义:
import java.lang.reflect.Array;
import java.util.Arrays;
public class BinarySearch2 {
public static void main(String[] args) {
int[] a={1,2,3};
int target=9;
int i = Arrays.binarySearch(a, target);
System.out.println(i);//-4
//-2=-插入点(索引位置)-1
//target=9:-4=-3-1
}
}基础版二分查找代码:
它的插入点位置可以用i表示
public class BinaarySearch {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length-1;//设置指针和初始值
while (i<=j){
//范围内有东西
// int m=(i+j)/2;
int m=(i+j)>>>1;
if (target4.1 按照升序向数组中插入某个元素
import java.lang.reflect.Array;
import java.util.Arrays;
public class BinarySearch2 {
public static void main(String[] args) {
int[] a={1,2,3};
int target=9;
int i = Arrays.binarySearch(a, target);
System.out.println(i);//-4
//-2=-插入点(索引位置)-1
//target=9:-4=-3-1
if (i<0){
int insertIndex=Math.abs(i+1);//插入索引值
int[] b=new int[a.length+1];
System.arraycopy(a,0,b,0,insertIndex);
b[insertIndex]=target;
System.arraycopy(a,insertIndex,b,insertIndex+1,a.length-insertIndex);
System.out.println(Arrays.toString(b));
}
}
}输出:
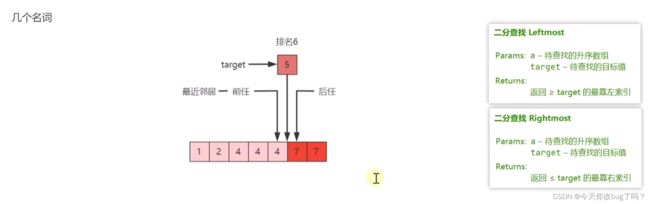
4.2 查找数组中重复元素最左侧的元素索引
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length;//第一处
int candidate=-1;
while (i>>1;
if (target 优化后代码:
若能找到:返回数组中重复元素最左侧的元素索引
若不能找到:返回比目标大的最靠左的元素索引
所以,i的含义是大于等于目标值的最靠左的索引位置
public class BinarySearchLeft2 {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length;//第一处
while (i>>1;
if (target<=a[m]){
j=m;//第三处
} else if ( a[m]< target) {
i=m+1;
}
}
return i;
}
} 4.3 查找数组中重复元素最右侧的元素索引
public class BinarySearchRight {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length;//第一处
int candidate=-1;
while (i>>1;
if (target 优化后代码:
i-1含义:小于等于目标值的最靠右的索引位置
public class BinarySearchRight2 {
public static int binarySearchBasic(int[] a,int target){
int i=0;
int j=a.length;//第一处
while (i>>1;
if (target<=a[m]){
j=m;//第三处
} else if ( a[m]< target) {
i=m+1;
}
}
return i-1;
}
} 五、二分查找的应用
LeftRightMost应用:
练习一:二分查找
给定一个n个元素有序的(升序)整型数组nums和一个目标值 target,写一个函数搜索 nums 中的 target ,如果目标值存在返回下标,否则返回 -1。
提示:
1.你可以假设 nums中的所有元素是不重复的
2.n将在[1,10000]之间。
3.nums 的每个元素都将在[-9999,9999] 之间。
答案一:基础版
public class BinarySearchTest1 {
public int search(int[] nums,int target){
int i=0;
int j=nums.length-1;
while (i<=j){
int m=(i+j)>>>1;
if (target答案二:改动版
public class BinarySearchTest1 {
public int search(int[] nums,int target){
int i=0;
int j=nums.length;
while (i>>1;
if (target 答案三:平衡版
public class BinarySearchTest1 {
public int search(int[] nums,int target){
int i=0;
int j=nums.length;
while (i+1>>1;
if (target 练习二:搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为O(log n)的算法
提示:
- 1 <= nums.length <=10^4
- -10^4<= nums[i] <= 10^4
- nums为无重复元素的升序排列数组
- -10^4 <= target <= 10^4
答案一:
public class BinarySearchTest2 {
public int searchInsert(int[] nums,int target){
int low=0;
int high=nums.length-1;
while (low<=high){
int mid=(low+high)>>>1;
long midVal=nums[mid];
if (midVal target) {
high=mid-1;
}else {
return mid;//target found
}
}
return -(low+1);//target not found
}
} 答案二:
public class BinarySearchTest2 {
public int searchInsert(int[] nums,int target){
int low=0;
int high=nums.length-1;
while (low<=high){
int mid=(low+high)>>>1;
long midVal=nums[mid];
if (midVal= target) {
high=mid-1;
}
}
return low;//target not found
}
} 练习三:搜索开始结束位置
给你一个按照非递减顺序排列的整数数组 nums,和一个标值 target 。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target ,返回 [-1,-1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
提示:
- 0<= nums.length <= 10^5
- -10^9<= nums[i]<= 10^9
- nums是一个非递减数组
- -10^9<= target <= 10^9
public class BinarySearchTest3 {
public int[] searchRange(int[] nums,int target){
int x = left(nums, target);
if (x==-1){
return new int[]{-1,-1};
}else {
return new int[]{x,right(nums,target)};
}
}
public int left(int[] nums,int target){
int i=0,j=nums.length-1;
int candidate=-1;
while (i<=j){
int m=(i+j)>>>1;
if (target>>1;
if (target