408数据结构学习笔记——二叉排序树、二叉平衡树、红黑树

目录

1.二叉排序树 

1.1.二叉排序树的基本概念

1.2.二叉排序树的查找代码实现

1.3.二叉排序树的插入

1.4.二叉排序树的删除

1.5.二叉排序树的查找效率

1.6.二叉排序树的缺陷

2.平衡二叉树

2.1.平衡二叉树的基本概念

2.2.平衡二叉树的插入

2.2.1.LL型平衡旋转（中为支，高右转）

2.2.2.RR型平衡旋转（中为支，高左转）

2.2.3.LR型平衡旋转（下二整体先左转，后与LL同）

2.2.4.RL型平衡旋转（下二整体先右转，后与RR相同）

2.2.5.平衡二叉树插入手算示例

2.3.平衡二叉树的查找效率分析

2.4.平衡二叉树的缺陷

2.5.平衡二叉树的删除

3.红黑树

3.1.红黑树的基本概念（左根右，根叶黑，不红红，黑路同）

3.2.红黑树的性质

3.3.红黑树的插入

3.3.1.红黑树的插入规则

3.3.2.红黑树的插入特点

3.3.2.红黑树的插入手算示例

4.王道课后题

---

1.二叉排序树 

1.1.二叉排序树的基本概念

1.左子树结点值 < 根结点值 < 右子树结点值，且它的左右子树又递归的满足这一特性

2.对二叉排序树进行中序遍历，得到的序列是递增的有序序列

1.2.二叉排序树的查找代码实现

1.树非空，则与当前根结点进行匹配；空则返回

2.根结点比key大，去左子树；根结点比key小，去右子树

3.相等则，返回；不相等则继续1、2

typedef struct BSTNode{
    elemtype data;
    struct BSTNode *rchild, *lchild;
}BSTNode, *BSTree;

BSTNode *Search(BSTree T, int key){
    //当T为空或者T的data域与key相等时结束循环
    while (T && key != T->data){
        //当前T的data比key大则去左子树，比key小则去右子树
        if (T->data > key) T = T->lchild;
        else T = T->rchild;
    }
    return T;
}

//递归调用
typedef struct BiNode{
    struct BiTNode *lchild, *rchild;
    int value;
}BiTNode, *BiTree;

BiTNode* Search(BiTree T, int key) {
    BiTNode* p = NULL;
    if (!T) return NULL;
    else if (T->value == key) {
        return T;
    }
    else if (T->value < key) {
        p = Search(T->rchild, key);
    }
    else p = Search(T->lchild, key);
}

空间复杂度：非递归O(1)，递归O(n)

1.3.二叉排序树的插入

typedef struct BSTNode{
    struct BSTNode *lchild, *rchild;
    elemtype value;
}BSTNode, BSTree;

bool Insert(BSTree &T, int e){
    //当前根结点为空
    if (T == NULL) {
        T = (BSTNode*)malloc(sizeof(BSTNode));
        T->value = e;
        T->rchild = NULL;
        T->lchild = NULL;
        return true;
    }
    else if (T->value == e) return false;
    else if (T->value > e) return Insert(T->lchild, e);
    else return Insert(T->rchild, e);
}

相同的关键字不同的顺序，可能构造不同的排序二叉树

1.4.二叉排序树的删除

1.删除叶子结点：直接删除

2.删除只有左子树或只有右子树的结点：让其子树的根节点代替

3.删除有左右子树的结点：根据中序遍历的特性，替换成直接前驱或直接后继

planA：替换成直接后继。找到其右子树的最左下的结点替换（最左下即该结点一定没有左孩子），而被替换的结点由它的右子树的根节点代替（转换成2）

planB：替换成直接前驱。找到其左子树的最右下的结点替换（最右下即该结点一定没有右孩子），而被替换的结点由它的左子树的根节点代替（转换成2）

排序二叉树删除叶子结点后重新加入：不会改变树形结构

排序二叉树删除分支结点后重新加入：一定改变树形结构

1.5.二叉排序树的查找效率

最好情况：O()，与树高相关（与折半查找类似）

最坏情况：O(n)，单边树，即每层都只有一个结点（折半查找是平衡二叉树，不可能出现单边）

1.6.二叉排序树的缺陷

可能会出现单支树，严重影响查找效率

2.平衡二叉树

2.1.平衡二叉树的基本概念

平衡二叉树（AVL）上的任一个结点的左右子树的高度差的绝对值不超过1（左子树高度减右子树高度，即平衡因子）

2.2.平衡二叉树的插入

强烈推荐这个up的二叉树的调整！

二叉平衡树AVL平衡调整数据结构_哔哩哔哩_bilibili-https://www.bilibili.com/video/BV1xE411h7dd?spm_id_from=333.337.search-card.all.click找插入后失去平衡的最小子树

1.该子树是失去平衡的所有子树中距离插入结点最近的子树

2.平衡因子绝对值大于1的结点作为根

2.2.1.LL型平衡旋转（中为支，高右转）

加入BL后，子树的平衡因子为2，失去平衡。以中间结点为支点（根节点），高结点向右转（顺时针）

2.2.2.RR型平衡旋转（中为支，高左转）

加入BR后，子树的平衡因子为2，失去平衡。以中间结点为支点（根节点），高结点向左转（逆时针）

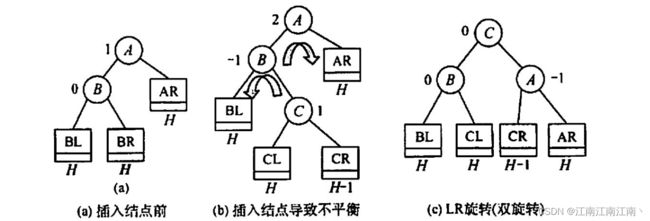
2.2.3.LR型平衡旋转（下二整体先左转，后与LL同）

加入C后，子树的平衡因子为2，失去平衡

1.调整子树BC。BC向左转（逆时针），旋转后，C为A的左子树，B为C的左子树（调整为LL型）

2.调整子树ACB。以C为支点（根节点），向右旋转（顺时针）（LL型平衡旋转）

2.2.4.RL型平衡旋转（下二整体先右转，后与RR相同）

加入C后，子树的平衡因子为2，失去平衡

1.调整子树BC。BC向右转（顺时针），旋转后，C为A的右子树，B为C的右子树（调整为RR型）

2.调整子树ACB。以C为支点（根节点），向左旋转（顺时针）（RR型平衡旋转）

2.2.5.平衡二叉树插入手算示例

2.3.平衡二叉树的查找效率分析

设高度为h平衡二叉树的结点个数至少为，则  =  +  + 1

因此，平均二叉树的最大深度为O()，则平均查找长度为O()

2.4.平衡二叉树的缺陷

平衡二叉树的插入/删除操作，很容易破坏树的平衡姿态。若导致不平衡，则要计算平衡因子、找到最小不平衡树，时间开销大

2.5.平衡二叉树的删除

删除叶子结点后再将此结点插入，不一定不改变树的结构：如果删除后影响平衡，进行树形调整，则会再插入时，树的某些结点就会不一样

删除分之结点后再将此结点插入，并非一定改变树的结构：删除后，树形会发生变化，由其前驱或者后继补上其的位置，但是，在重新加入后，有可能影响某些子树的平衡，导致重新调整为删除前的树形结构

3.红黑树

3.1.红黑树的基本概念（左根右，根叶黑，不红红，黑路同）

1.红黑树的插入/删除操作一般无需调整树的形态（调整也是常数级）

2.红黑树是二叉排序树，即左 < 根 < 右（左根右）

3.每个结点都只能为红/黑

4.根节点为黑、叶子结点为黑（叶子结点指的是失败结点、NULL结点，而非度为0的结点）（图中画圈） （根叶黑）

6.不存在两个相邻的红结点（红结点的双亲结点和孩子结点必须为黑结点）（不红红）

7.对于每个结点，该结点到任一叶子结点的简单路径上黑结点数相同（黑路同）

8.黑高：从该结点到叶子结点经过的黑结点的总数

3.2.红黑树的性质

1.从根节点到叶结点的最长路径不大于最短路径的2倍

最长路径：红黑红黑交替

最短路径：全黑

2.红黑树的高度 h <= 

3.3.红黑树的插入

3.3.1.红黑树的插入规则

1.找到插入位置（同二叉排序树一样）

2.新结点是根：染为黑色

新结点非根：染为红色

(1)新插入的结点满足红黑树定义，则插入结束（不红红或根非黑）

(2)新插入的结点不满足红黑树的定义：查看叔结点

a.叔为黑：旋转＋染色。按照平衡二叉树的LL、RR、LR、RL型进行对应旋转，并且被改变位置的结点的颜色进行改变——红变黑、黑变红

b.叔为红：染色＋变新。叔父爷染色，并且爷变为新结点（需要重新判断爷是否为根节点和颜色）

3.3.2.红黑树的插入特点

插入的过程中，只有不红红这一特性会被破坏，因此，只需注意这一特性，原因：

1.左根右：插入的位置都满足左 < 根 < 右

2.根叶黑：红黑树中叶子结点是NULL，而被插入的结点是NULL上面的度为0的结点

3.黑路同：每次加入的非根结点首先都被染成红色（插入结点开始染色成红色就是为了这一个特性不会被破坏），不会改变路径上黑色数量

3.3.2.红黑树的插入手算示例

4.王道课后题

查找成功的平均查找长度：（1 * 1 + 2 * 2 + 4 * 3 + 3 * 4）/ 10 = 2.9

查找失败的平均查找长度：（5 * 3 + 6 * 4）/ 11 = 39 / 11

查找成功的平均查找长度：（1 * 1 + 2 * 2 + 3 * 3 + 2 * 4 + 5 * 2）/ 10 = 3.2 

 从小到打的顺序排列关键字，然后仿照折半查生成树的规则建立该二叉排序树

大根堆的要求是：根节点为整个树中最大的结点

二叉排序树的要求是：左 < 根 < 右

因此，只能是一个结点或两个结点（根节点+左孩子）的树 

判断是否为排序二叉树利用排序二叉树中序遍历是一个递增的有序序列的特性

递归实现 

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

//用于标记上一个结点的值
elemtype temp;

bool IsBST(BiTree T) {
    int left, right;
    //空树为二叉排序树的特殊情况
    if (!T) return true;
    else {
        //访问左子树
        left = IsBST(T->lchild);
        //当前结点的左子树不满足排序二叉树或当前结点不满足左 < 根 < 右
        if (!left || temp > T->value) return false;
        //更新temp值
        temp = T->value;
        //访问右子树
        right = IsBST(T->rchild);
        //返回右子树的结果
        if (right) return true;
        else return false;
    }
}

非递归实现

#define MAXSIZE 100

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

typedef struct Stack{
    BiTNode data[MAXSIZE];
    int top;
}

bool IsBST(BiTree T){
    Stack S;
    InitStack(S);
    BiTNode *p = T;
    //初始化temp的值为-1
    elemtype temp = -1;
    while(p || !IsEmpty(S)){
        if (p){
            //压入栈中
            push(S, p);
            //进入左子树
            p = p->lchild;
        }
        else {
            //从栈中弹出元素
            pop(S, p);
            //不是中序序列的第一个结点则进行比较
            if (temp != -1) {
                if (temp > p->value) return false;
            }
            //更新temp的值
            temp = p->value;
            //进入右子树
            p = p->rchild;
        }//else
    }//while
}

递归实现 

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

int CurrentLevel(BiTree T, int key, int cur) {
    int res;
    //当前结点等于key，返回当前层数
    if (T->value == key) return cur;
    //当前结点比key小，去右子树查找
    else if (T->value < key) res = CurrentLevel(T->rchild, key, cur + 1);
    //当前结点比key大，去左子树查找
    else res = CurrentLevel(T->lchild, key, cur + 1);
    return res;
}

//函数入口
int SearchEntry(BiTree T, int key) {
    int res = CurrentLevel(T, key, 1);
    return res;
}

非递归实现 

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

int CurrentLevel(BiTree T, elemtype key){
    BiTNode *p = T;
    int res = 0;
    //非空树
    if (p){
        //当前层数++
        res++;
        //循环遍历直到找到key
        while(p->value == key){
            //当前结点比key小，去右子树；否则去左子树
            if (p->value < key) p = p->rchild;
            else p = p->lchild;
            //当前层数++
            res++;
        }//while
    }
    return res;
}

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtypede value;
}BiTNode, *BiTree;

//计算绝对值
int Inverse(int t){
    if(t >= 0 ) return t;
    else return -t;
}

void IsBalance(BiTree T, int &curH, int &balance){
    //左高，右高，左平衡，右平衡
    int lHigh = 0, rHigh = 0, lBalance = 0, rBalance;
    //空结点，高度为0，平衡
    if (!T){
        balance = 1;
        curH = 0;
    }
    //叶子结点，高度为0，平衡
    else if (!T->lchild && !T->rchild) {
        balance = 1;
        curH = 1;
    }
    //分支节点
    else {
        //进入左子树
        if (T->lchild) IsBalance(T, lHigh, lBalance);
        //进入右子树
        if (T->rchild) IsBalance(T, rHigh, rBalance);
        //更改上一层的高度
        curH = (lHigh > rHigh ? lHigh : rHigh) + 1;
        //计算平衡值的绝对值
        int temp = Inverse(lHigh - rHigh);
        //当前平衡值小于等于1
        if (temp <= 1) {
            //左右是否平衡
            if (lBalance && rBalance) Balance = 1;
        //不平衡
        else balance = 0;
    }
}

二叉排序树中的最小值在最左结点，二叉排序树的最大值在最右结点

#define INT_MAX 0x7fffffff
#define INT_MIN (-INT_MAX - 1)

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

//保存最大值和最小值
int max = INT_MIN, min = INT_MAX;
void Search(BiTree T){
    if (!T) return;
    BiTNode *p = T;
    while(p) {
        min = p->value;
        p = p->lchild;
    }
    p = T;
    while(p) {
        max = p->value;
        p = p->rchild;
    }
}

右根左的顺序遍历排序二叉树

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
}BiTNode, *BiTree;

void GatherThanKey(BiTree T, int key) {
    if (T) {
        //遍历右子树
        GatherThanKey(T->rchild, key);
        //判断当前结点是否大于key
        if (T->value > key) cout << T->value << endl;
        //遍历左子树
        GatherThanKey(T->lchild, key);
    }
}

typedef struct BiTNode{
    struct BiTNode *lchild, *rchild;
    elemtype value;
    int count;
}BiTNode, *BiTree;

BiTNode *SearchK(BiTree T, int k) {
    //k不合法
    if (k < 1 || k > T->count) return;
    //当前结点的左子树不存在
    if (!T->lchild) {
        //当前k = 1，则是第k个结点
        if (k == 1) return T;
        //否则进入右子树
        else return SearchK(T->rchild, k - 1);
    }
    else {    //左子树存在
        //左子树的结点个数为count个，加上根节点，因此，当k = count + 1时，根节点是第k个结点
        if (k == T->lchild->count + 1) return T;
        //k > count + 1，进入右子树
        if (k > T->lchild->count + 1) return SearchK(T->rchild, k - T->lchild->count - 1);
        //k < count - 1，进入左子树
        if (k < T->lchild->count + 1) return SearchK(T->lchild, k);
    }
}