机器学习算法理论：线性回归

线性回归

       回归的理论解释：回归分析是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法。按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

       如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

使用线性回归时，需要遵循以下假设：

• 要预测的因变量与自变量的关系是线性的。
• 假设每个观测值之间是相互独立的。
• 假设在自变量的每个取值点上，误差方差都是常数。
• 各项误差服从正态分布。

最小二乘法

以房价预测为例。 

目标：给定房屋面积和房龄准确预测房价。

房屋面积（）	房龄（）	房价（）
64	2	709000
100	3	1060000
87	5	902000
78	7	854000

 根据以上房价为数据样本，假设：

其中： 

• 为真实房价（标签）
• 为微调模型的参数（偏置）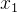
• 为房屋面积（特征）
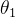• 为房屋面积在房价中影响究竟有多大（权重）
• 为房龄（特征）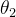
• 为房龄在房价中影响究竟有多大（权重）

向量表示：

 

在对每个样本进行计算都会产生一个预测值，预测值与真实值之间产生误差值。误差项通常以来表示，则：

所以求解的目标：就是让误差项最小，甚至为0。而每条样本产生的误差都是独立同分布的（独立是指每套房子房价是独立的，同分布是指每套房子是在同一行情下），并且服从均值为0方差为的正态分布。则：

 根据前面的公式：可得： 再与以上公式合并可得：

此时求解的目标为： 在给定了和时，得到的真实值的概率最大。

根据以上目标得到似然函数：

可以理解为所有样本预测值接近真实值概率的乘积。

为方便求解将以上公式转化为对数似然函数(添加对数不影响求解目标，因为我们要得到的是一个点，而不是点对应的值)：

           

因和  是常数，所以目标函数转化为： 

再将目标函数转化为最小二乘法根据偏导数等于0求解：

 

接下来求偏导：

令偏导数为0，则得到：

以上是使用最小二乘法求解，接下来将通过梯度下降的方法进行不断学习来逐步优化参数θ。

梯度下降 

梯度下降法是一种常用的优化算法，用于求解目标函数的最小值。其基本原理是通过迭代的方式，不断更新参数的值，使得目标函数的值逐渐趋近于最小值。梯度下降法的核心思想是利用函数的梯度信息来指导参数的更新方向 。

常用的梯度下降方法

---

批量梯度下降法：这种方法计算整个数据集的梯度，然后更新参数。每个参数的更新都是整个数据集上的平均值。然而，这种方法计算量大，计算速度慢，尤其当数据集很大时。

import numpy as np

# 生成模拟数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X + 1 + 0.1 * np.random.randn(100, 1)

# 初始化参数
theta = np.random.randn(2, 1)
alpha = 0.01  # 学习率
iterations = 1000  # 迭代次数
m = len(y)  # 样本数量

# 批量梯度下降法
for i in range(iterations):
    gradients = 2 / m * X.T.dot(X.dot(theta) - y)  # 计算梯度
    theta = theta - alpha * gradients  # 更新参数

print("Theta:", theta)

随机梯度下降法：这种方法每次只使用一个样本计算梯度，然后更新参数。这种方法计算速度快，但是存在一定的随机性，可能会导致收敛速度慢或者无法收敛到全局最优解。

import numpy as np

def sgd(X, y, learning_rate=0.01, epochs=100):
    # 获取输入矩阵的行数和列数
    m, n = X.shape
    # 初始化参数向量theta为全零向量
    theta = np.zeros(n)
    # 进行指定轮数的迭代更新
    for _ in range(epochs):
        # 遍历数据集中的每个样本
        for i in range(m):
            # 随机选择一个样本
            rand_idx = np.random.randint(m)
            xi = X[rand_idx:rand_idx+1]
            yi = y[rand_idx:rand_idx+1]
            # 计算梯度
            gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
            # 更新参数向量theta
            theta = theta - learning_rate * gradients
    # 返回训练得到的参数向量theta
    return theta

# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 训练模型
theta = sgd(X, y)
print("Theta:", theta)

小批量梯度下降法：这种方法介于批量梯度下降法和随机梯度下降法之间，使用一部分数据（小批量）计算梯度，然后更新参数。这种方法计算速度较快，且能得到较好的优化效果。

import numpy as np

# 定义小批量梯度下降法函数
def mini_batch_gradient_descent(X, y, learning_rate=0.01, epochs=100, batch_size=32):
    # 获取样本数量和特征数量
    m, n = X.shape
    
    # 初始化参数向量
    theta = np.zeros((n, 1))
    
    # 迭代更新参数
    for epoch in range(epochs):
        # 随机打乱样本顺序
        permutation = np.random.permutation(m)
        X_shuffled = X[permutation]
        y_shuffled = y[permutation]
        
        # 将数据集划分为小批量
        for i in range(0, m, batch_size):
            X_batch = X_shuffled[i:i+batch_size]
            y_batch = y_shuffled[i:i+batch_size]
            
            # 计算梯度
            gradient = (1/batch_size) * X_batch.T @ (X_batch @ theta - y_batch)
            
            # 更新参数
            theta -= learning_rate * gradient
            
    return theta

# 示例数据
X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
y = np.array([[3], [7], [11], [15]])

# 调用小批量梯度下降法函数进行线性回归
theta = mini_batch_gradient_descent(X, y)
print("拟合参数：", theta)

动量梯度下降法：这种方法在每次迭代中不仅考虑当前的梯度，还考虑上次迭代的梯度方向，从而加速收敛速度并减少震荡。动量项的引入可以使得算法在优化过程中具有一定的记忆性，能够沿着之前的下降方向继续前进。

import numpy as np

def momentum_gradient_descent(X, y, learning_rate=0.01, momentum=0.9, num_iterations=100):
    """
    使用动量梯度下降法求解线性回归问题。

    参数：
    X -- 输入数据矩阵 (m x n)
    y -- 目标变量向量 (m x 1)
    learning_rate -- 学习率 (默认值为0.01)
    momentum -- 动量系数 (默认值为0.9)
    num_iterations -- 迭代次数 (默认值为100)

    返回：
    theta -- 最优参数向量 (n x 1)
    """
    # 初始化参数向量和动量向量
    m, n = X.shape
    theta = np.zeros((n, 1))
    velocity = np.zeros((n, 1))

    # 迭代更新参数
    for i in range(num_iterations):
        # 计算梯度
        gradient = (1 / m) * X.T @ (X @ theta - y)

        # 更新动量向量
        velocity = momentum * velocity + learning_rate * gradient

        # 更新参数向量
        theta = theta - velocity

    return theta

Adam：Adam 算法是一种自适应学习率的优化算法，结合了动量梯度下降法和 RMSProp 算法的特点。它通过计算梯度的指数移动平均值来调整学习率，以更好地适应不同参数的更新速度。Adam 算法在许多任务中表现出色，被广泛应用于深度学习模型的训练。