史诗级干货长文---K近邻算法
本文将从KNN算法的思想讲起,使用python3进行实战训练。
KNN简介
k近邻法工作原理是:存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知道样本集中每一个数据与所属分类的对应关系。输入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。一般来说,我们只选择样本数据集中前k个最相似的数据,这就是k-近邻算法中k的出处,通常k是不大于20的整数。最后,选择k个最相似数据中出现次数最多的分类,作为新数据的分类。
一般实现步骤如下:
- 计算已知类别数据集中的点与当前点之间的距离;
- 按照距离递增次序排序;
- 选取与当前点距离最小的k个点;
- 确定前k个点所在类别的出现频率;
- 返回前k个点所出现频率最高的类别作为当前点的预测分类。
在上面算法简述当中,其实我们可以知道k邻近核心思想非常简单即给定测试样本,然后基于某种距离度量找出训练集中与其最靠近的k个样本,然后基于这k个样本的信息来进行预测。通常在进行分类任务时,是选择k个样本中出现最多的类别标记作为预测结果。总结起来就是“近朱者赤,近墨者黑”。
举一个简单的例子,可以通过k邻近算法分类一个电影时爱情片还是动作片
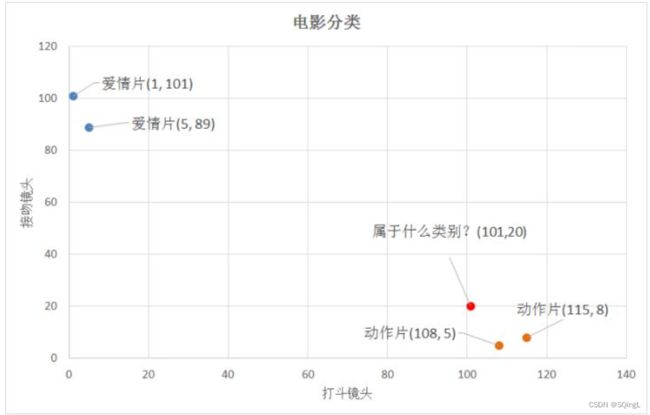
表中是已有的数据集合,也就是训练样本集。这个数据集有两个特征,即打斗镜头数和接吻镜头数。除此之外,也知道每个电影的所属类型,即分类标签。用肉眼粗略地观察,接吻镜头多的,是爱情片。打斗镜头多的,是动作片。以我们多年的看片经验,这个分类还算合理。如果现在给我一部电影,你告诉我这个电影打斗镜头数和接吻镜头数。不告诉我这个电影类型,我可以根据你给我的信息进行判断,这个电影是属于爱情片还是动作片。人眼和KNN不同的是在于我们拥有更丰富的数据,而KNN依靠数据。比如,这个电影打斗镜头数为2,接吻镜头数为102,经验会告诉你这个是爱情片,k-近邻算法也会告诉你这个是爱情片。你又告诉我另一个电影打斗镜头数为49,接吻镜头数为51,"邪恶"的经验可能会告诉你,这有可能是个"爱情动作片"。是k-近邻算法不会告诉你这些,因为在它的眼里,电影类型只有爱情片和动作片,它会提取样本集中特征最相似数据(最邻近)的分类标签,得到的结果可能是爱情片,也可能是动作片,但绝不会是"爱情动作片"。当然,这些取决于数据集的大小以及最近邻的判断标准等因素。
距离度量
k-近邻算法根据特征比较,然后提取样本集中特征最相似数据(最邻近)的分类标签。那么,如何进行比较呢?怎么判断红色圆点标记的电影所属的类别呢?
从散点图大致推断,这个红色圆点标记的电影可能属于动作片,因为距离已知的那两个动作片的圆点更近。k-近邻算法用什么方法进行判断呢?没错,就是距离度量。这个电影分类的例子有2个特征,也就是在2维实数向量空间,可以使用我们高中学过的两点距离公式计算距离。
通过计算,我们可以得到如下结果:
- (101,20)->动作片(108,5)的距离约为16.55
- (101,20)->动作片(115,8)的距离约为18.44
- (101,20)->爱情片(5,89)的距离约为118.22
- (101,20)->爱情片(1,101)的距离约为128.69
通过计算可知,红色圆点标记的电影到动作片 (108,5)的距离最近,为16.55。如果算法直接根据这个结果,判断该红色圆点标记的电影为动作片,这个算法就是最近邻算法,而非k-近邻算法。
回顾一下KNN的步骤:
- 计算已知类别数据集中的点与当前点之间的距离;
- 按照距离递增次序排序;
- 选取与当前点距离最小的k个点;
- 确定前k个点所在类别的出现频率;
- 返回前k个点所出现频率最高的类别作为当前点的预测分类。
比如,现在我这个k值取3,那么在电影例子中,按距离依次排序的三个点分别是动作片(108,5)、动作片(115,8)、爱情片(5,89)。在这三个点中,动作片出现的频率为三分之二,爱情片出现的频率为三分之一,所以该红色圆点标记的电影为动作片。这个判别过程就是k-近邻算法。
代码实现
对于表中的数据,可以使用numpy创建
# -*- coding: UTF-8 -*-
import numpy as np
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#打印数据集
print(group)
print(labels)代码运行结果如图所示:
根据两点距离公式,计算距离,选择距离最小的前k个点,并返回分类结果。
# -*- coding: UTF-8 -*-
import numpy as np
import operator
def createDataSet():
#四组二维特征
group = np.array([[1,101],[5,89],[108,5],[115,8]])
#四组特征的标签
labels = ['爱情片','爱情片','动作片','动作片']
return group, labels
def classify0(inX, dataSet, labels, k):
#numpy函数shape[0]返回dataSet的行数
dataSetSize = dataSet.shape[0]
#在列向量方向上重复inX共1次(横向),行向量方向上重复inX共dataSetSize次(纵向)
diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
#二维特征相减后平方
sqDiffMat = diffMat**2
#sum()所有元素相加,sum(0)列相加,sum(1)行相加
sqDistances = sqDiffMat.sum(axis=1)
#开方,计算出距离
distances = sqDistances**0.5
#返回distances中元素从小到大排序后的索引值
sortedDistIndices = distances.argsort()
#定一个记录类别次数的字典
classCount = {}
for i in range(k):
#取出前k个元素的类别
voteIlabel = labels[sortedDistIndices[i]]
#dict.get(key,default=None),字典的get()方法,返回指定键的值,如果值不在字典中返回默认值。
#计算类别次数
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
#python3中用items()替换python2中的iteritems()
#key=operator.itemgetter(1)根据字典的值进行排序
#key=operator.itemgetter(0)根据字典的键进行排序
#reverse降序排序字典
sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
#返回次数最多的类别,即所要分类的类别
return sortedClassCount[0][0]
if __name__ == '__main__':
#创建数据集
group, labels = createDataSet()
#测试集
test = [101,20]
#kNN分类
test_class = classify0(test, group, labels, 3)
#打印分类结果
print(test_class)代码运行结果
到这里,也许有人早已经发现,电影例子中的特征是2维的,这样的距离度量可以用两 点距离公式计算,但是如果是更高维的呢?对,没错。我们可以用欧氏距离(也称欧几里德度)。我们高中所学的两点距离公式就是欧氏距离在二维空间上的公式,也就是欧氏距离的n的值为2的情况。
也不难发现,k-近邻算法没有进行数据的训练,直接使用未知的数据与已知的数据进行比较,得到结果。因此,可以说k-近邻算法不具有显式的学习过程。
k-近邻算法实战之约会网站配对效果判定
上述为简单的k-近邻算法的实现方法,但是这并不是完整的k-近邻算法流程,k-近邻算法的一般流程:
- 收集数据:可以使用爬虫进行数据的收集,也可以使用第三方提供的免费或收费的数据。一般来讲,数据放在txt文本文件中,按照一定的格式进行存储,便于解析及处理。
- 准备数据:使用Python解析、预处理数据。
- 分析数据:可以使用很多方法对数据进行分析,例如使用Matplotlib将数据可视化。
- 测试算法:计算错误率。
- 使用算法:错误率在可接受范围内,就可以运行k-近邻算法进行分类。
下面进入实战内容:
# 导入数据集
datingTest = pd.read_table('datingTestSet.txt',header=None)
datingTest.head()
# 分析数据
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
#把不同标签用颜色区分
Colors = []
for i in range(datingTest.shape[0]):
m = datingTest.iloc[i,-1] # 标签
if m=='didntLike':
Colors.append('black')
if m=='smallDoses':
Colors.append('orange')
if m=='largeDoses':
Colors.append('red')
#绘制两两特征之间的散点图
plt.rcParams['font.sans-serif']=['Simhei'] #图中字体设置为黑体
pl=plt.figure(figsize=(12,8)) # 建立一个画布
fig1=pl.add_subplot(221) # 建立两行两列画布,放在第一个里面
plt.scatter(datingTest.iloc[:,1],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('玩游戏视频所占时间比')
plt.ylabel('每周消费冰淇淋公升数')
fig2=pl.add_subplot(222)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,1],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('玩游戏视频所占时间比')
fig3=pl.add_subplot(223)
plt.scatter(datingTest.iloc[:,0],datingTest.iloc[:,2],marker='.',c=Colors)
plt.xlabel('每年飞行常客里程')
plt.ylabel('每周消费冰淇淋公升数')
plt.show()
# 数据归一化
def minmax(dataSet):
minDf = dataSet.min()
maxDf = dataSet.max()
normSet = (dataSet - minDf )/(maxDf - minDf)
return normSet
datingT = pd.concat([minmax(datingTest.iloc[:, :3]), datingTest.iloc[:,3]], axis=1)
datingT.head()
# 切分训练集和测试集
def randSplit(dataSet,rate=0.9):
n = dataSet.shape[0]
m = int(n*rate)
train = dataSet.iloc[:m,:]
test = dataSet.iloc[m:,:]
test.index = range(test.shape[0])
return train,test
train,test = randSplit(datingT)
# 分类器针对约会网站的测试代码
def datingClass(train,test,k):
n = train.shape[1] - 1 # 将标签列减掉
m = test.shape[0] # 行数
result = []
for i in range(m):
dist = list((((train.iloc[:, :n] - test.iloc[i, :n]) ** 2).sum(1))**5)
dist_l = pd.DataFrame({'dist': dist, 'labels': (train.iloc[:, n])})
dr = dist_l.sort_values(by = 'dist')[: k]
re = dr.loc[:, 'labels'].value_counts()
result.append(re.index[0])
result = pd.Series(result)
test['predict'] = result # 增加一列
acc = (test.iloc[:,-1]==test.iloc[:,-2]).mean()
print(f'模型预测准确率为{acc}')
return test
datingClass(train,test,5) # 95%
手写数字识别
import os
#得到标记好的训练集
def get_train():
path = 'digits/trainingDigits'
trainingFileList = os.listdir(path)
train = pd.DataFrame()
img = [] # 第一列原来的图像转换为图片里面0和1,一行
labels = [] # 第二列原来的标签
for i in range(len(trainingFileList)):
filename = trainingFileList[i]
txt = pd.read_csv(f'digits/trainingDigits/{filename}', header = None) #32行
num = ''
# 将32行转变为1行
for i in range(txt.shape[0]):
num += txt.iloc[i,:]
img.append(num[0])
filelable = filename.split('_')[0]
labels.append(filelable)
train['img'] = img
train['labels'] = labels
return train
train = get_train()
# 得到标记好的测试集
def get_test():
path = 'digits/testDigits'
testFileList = os.listdir(path)
test = pd.DataFrame()
img = [] # 第一列原来的图像转换为图片里面0和1,一行
labels = [] # 第二列原来的标签
for i in range(len(testFileList)):
filename = testFileList[i]
txt = pd.read_csv(f'digits/testDigits/{filename}', header = None) #32行
num = ''
# 将32行转变为1行
for i in range(txt.shape[0]):
num += txt.iloc[i,:]
img.append(num[0])
filelable = filename.split('_')[0]
labels.append(filelable)
test['img'] = img
test['labels'] = labels
return test
test = get_test()
# 分类器针对手写数字的测试代码
from Levenshtein import hamming
def handwritingClass(train, test, k):
n = train.shape[0]
m = test.shape[0]
result = []
for i in range(m):
dist = []
for j in range(n):
d = str(hamming(train.iloc[j,0], test.iloc[i,0]))
dist.append(d)
dist_l = pd.DataFrame({'dist':dist, 'labels':(train.iloc[:,1])})
dr = dist_l.sort_values(by='dist')[:k]
re = dr.loc[:,'labels'].value_counts()
result.append(re.index[0])
result = pd.Series(result)
test['predict'] = result
acc = (test.iloc[:,-1] == test.iloc[:,-2]).mean()
print(f'模型预测准确率为{acc}')
return test
handwritingClass(train, test, 3) # 97.8%
算法优缺点
优点
(1)简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;
(2)可用于数值型数据和离散型数据;
(3)无数据输入假定;
(4)适合对稀有事件进行分类。
缺点
(1)计算复杂性高;空间复杂性高;
(2)计算量大,所以一般数值很大的适合不用这个,但是单个样本又不能太少,否则容易发生误分;
(3)样本不平衡问题(即有些类别的样本数量很多,而其他样本的数量很少);
(4)可理解性比较差,无法给出数据的内在含义