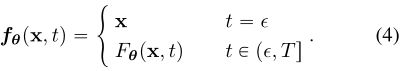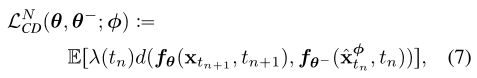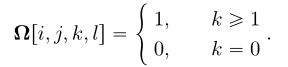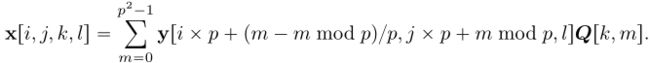Consistency Models终结扩散模型

　最近看到一篇论文，觉得特别有意思，并且在学术界引起了不小的动静，他就是一致性模型，据说图像生成效果快、质量高，并且还可以实现零样本图像编辑，即不进行一些视觉任务训练，可以实现图像超分、修复、上色等功能。

　　目前代码已经开源到GitHub上面： GitHub - openai/consistency_models: Official repo for consistency models.

1.介绍

　　扩散模型在图像、音频和视频生成方面取得了重大突破，但它们依赖于迭代生成过程，导致采样速度较慢，限制了其实时应用的潜力。为了克服这一限制，我们提出了一致性模型，这是一种新的生成模型家族，可以在没有对抗性训练的情况下实现高样本质量。它们在设计上支持快速的一步生成，同时仍然允许少步采样以换取样本质量的计算。它们还支持零样本数据编辑，如图像修补、着色和超分辨率，而不需要对这些任务进行明确的训练。

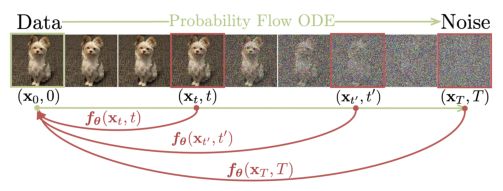
　　我们的目标是创建生成模型，以促进高效的单步生成，而不牺牲迭代细化的重要优势。这些优点包括在必要时为样本质量权衡计算的能力，以及执行零样本数据编辑任务的能力。如图1所示，我们建立在连续时间扩散模型中的概率流(PF)常微分方程(ODE)之上，其轨迹平滑地将数据分布转换为可处理的噪声分布。我们建议学习一个模型，将任何时间步骤的任何点映射到轨迹的起点。我们的模型的一个显著特性是自一致性:同一轨迹上的点映射到相同的起始点。因此，我们把这样的模型称为一致性模型。

　　

2.扩散模型

　　一致性模型在很大程度上受到(连续时间)扩散模型理论的启发。扩散模型通过高斯扰动逐步将数据扰动为噪声来生成数据，然后通过连续的去噪步骤从噪声中创建样本。让

表示数据分布，扩散模型首先用随机微分方程(SDE)扩散

        

　　

和

分别为漂移系数和扩散系数，

为标准布朗运动，我们把xt的分布表示为

，结果是

。该SDE的一个显著性质是存在一个常微分方程(ODE)，Song等人称之为概率流(PF) ODE，其在t点采样的轨迹分布:

　　

　　

是

分数函数，因此扩散模型也被称为基于分数的生成模型

　　通常情况下，式(1)中的SDE设计使

接近于可处理的高斯分布。为了进行采样，我们首先通过分数匹配训练一个分数模型

，然后将其代入Eq.(2)，以获得PF ODE的经验估计，其形式为：

　　

　　我们称Eq.(3)为经验PF ODE。我们采样

来初始化经验PF ODE，用任何数值ODE求解器及时地反向求解它。

　　扩散模型的瓶颈在于采样速度慢。显然，使用ODE求解器进行采样需要对评分模型

进行多次评估，这是计算成本很高的。现有的快速采样方法包括更快的数值ODE求解器和蒸馏技术。ODE求解器仍然需要超过10个评估步骤来生成有竞争力的样本。大多数蒸馏方法，依赖于在蒸馏之前从扩散模型中收集大量的样本数据集，这本身就是计算成本很高的。据我们所知，唯一不受这一缺点影响的蒸馏方法是渐进蒸馏(PD)。

3.一致性模型

　　一致性模型是一种新型的生成模型，在其设计的核心支持单步生成，同时仍然允许迭代生成。一致性模型可以在蒸馏模式或隔离模式下训练。在前一种情况下，一致性模型将预先训练的扩散模型的知识提取到单步采样器中，显著提高了其他蒸馏方法的样品质量，同时允许零样本图像编辑应用。在后一种情况下，一致性模型是孤立地训练的，不依赖于预训练的扩散模型。这使得它们成为一种独立的新型生成模型。

　　定义：给定一个解轨迹式(2)中的PF ODE

，我们定义一致性函数为

一致性函数具有这样的性质：它的输出对于属于相同PF ODE轨迹的任意对

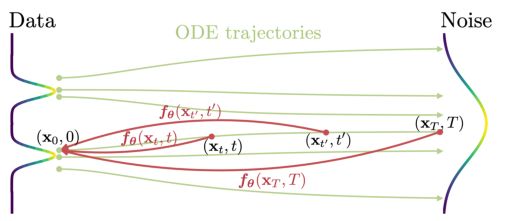
都是一致的，如图2所示，一致性模型的目标，用fθ表示，是通过学习加强一致性属性来估计数据中的一致性函数f。

　　

　　参数化：对于任何一致性函数

有

称这个约束为边界条件，一个有效的一致性模型必须尊重这个边界条件。对于基于深度神经网络的一致性模型，我们讨论了两种几乎免费实现该边界条件的方法。假设我们有一个自由形式的深度神经网络，其输出与x具有相同的维数。第一种方法是简单地将一致性模型参数化为：

　　

　　第二种方法是使用跳越连接对一致性模型进行参数化：

　　

　　采样：一个训练好的一致性模型

我们可以通过对初始分布进行采样来生成样本

，然后对一致性模型进行评价

，这只涉及通过一致性模型的一次向前传递，因此在一个步骤中生成样本，重要的是，还可以通过交替去噪和噪声注入步骤来多次评估一致性模型，以提高样本质量。在算法1中总结，这种多步采样过程提供了交换计算样本质量的灵活性。它在零样本数据编辑中也有重要的应用。

　　

　　零样本数据编辑：一致性模型可以在零样本数据编辑中实现各种数据编辑和操作应用;他们不需要明确的训练来完成这些任务。一致性模型定义了从高斯噪声向量到数据样本的一对一映射。一致性模型可以通过遍历潜在空间轻松地在样本之间进行插值，可以对各种噪声级进行去噪。此外，算法1中的多步生成过程可以通过使用类似于扩散模型的迭代替换过程来解决零射中的某些逆问题。这使得图像编辑上下文中的许多应用成为可能，包括修复、着色、超分辨率等。

4.通过蒸馏训练一致性模型

　　我们提出了基于提取预训练分数模型, 第一种训练一致性模型的方法。我们的讨论围绕式(3)中的经验PF ODE展开，它是通过将分数模型代入PF ODE得到的。在实践中，我们遵循Karras et al(2022)用公式确定边界

当N足够大时，我们可以通过运行数值ODE求解器的一个离散化步骤，从

获得

的准确估计。这个估计值，我们表示为

，定义为

　　

　　当使用欧拉求解器时，对应如下更新规则：

　　

　　为了简单起见，我们在这项工作中只考虑一步ODE求解器。将我们的框架推广到多步ODE求解器是很简单的，我们把它留作以后的工作。

　　给定一个数据点,我们可以生成一对相邻数据点

通过从数据集中采样x，有效地对PF ODE轨迹进行优化，紧随其后的是采样

从SDE的转变密度

,然后根据Eq.(6)，使用数值ODE求解器的一个离散步骤来计算

。然后，通过最小化一致性模型在

对上的输出差异来训练一致性模型。这促使我们遵循一致性蒸馏损失来训练一致性模型。

　　

　　用E[.]表示所有相关随机变量的期望。在我们的实验中，我们考虑了平方距离和l1距离

，以及习得的感知图像块相似性，发现

在所有测试中表现良好，我们通过对模型参数θ的随机梯度下降来最小化目标，同时用指数移动平均(EMA)更新θ´。也就是说，给定衰减率，我们在每个优化步骤后执行以下更新:

　　

　　我们把fθ´称为“目标网络”，fθ称为“在线网络”。我们发现，与简单设置θ´θ相比，Eq.(8)中的EMA更新和“stopgrad”算子可以极大地稳定训练过程，提高一致性模型的最终性能。

　　

5.隔离训练一致性模型

　　一致性模型可以不依赖于任何预训练的扩散模型进行训练，使一致性模型成为一个新的独立的生成模型家族。在一致性蒸馏中，我们使用预先训练好的评分模型来近似真实评分函数

。为了摆脱这种依赖，我们需要寻找其他方法来估计分数函数。事0实上，由于以下恒等式，存在

的无偏估计量：

　　

　　

我们可以得到蒙特卡罗估计

，这个估计实际上足以取代预先训练的扩散模型，进一步假设我们使用欧拉ODE求解器，预训练的分数模型与GT匹配

，即:

　　

　　一致性训练目标

，表示为

　　

　　

，如果

证明基于Taylor级数展开和分数函数的性质。我们将式(10)称为一致性训练(CT)损失。关键的是，loss只依赖于在线网络fθ和目标网络fθ´，而完全不依赖于扩散模型参数φ。

　　

6.实验

　　使用一致性蒸馏和一致性训练来学习真实图像数据集上的一致性模型，包括CIFAR-10 ， ImageNet， LSUN。根据FID(越低越好)，Inception Score (is, 越高越好)，Precision (Prec,越高越好)，以及Recall (Rec，越高越好)。

　　

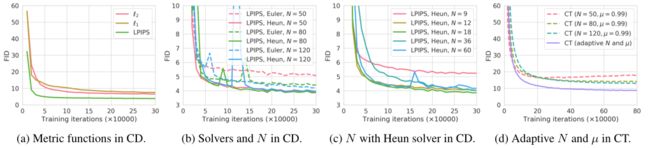
　　影响CIFAR-10一致性蒸馏(CD)和一致性训练(CT)的各种因素。CD的最佳配置是LPIPS, Heun ODE求解器和N=18。我们对N和µ的自适应调度函数使CT在优化过程中收敛速度明显快于将其固定为常数。由于CD和CT之间的紧密联系，本文采用LPIPS进行CT实验。与CD不同，在CT中不需要使用Heun的二阶求解器，因为损失函数不依赖于任何特定的数值ODE求解器。如图3d所示，CT的收敛对N高度敏感，N越小收敛速度越快，但得到的样本越差，N越大收敛速度越慢，收敛后得到的样本越好。这与我们在第5节中的分析相匹配，并促使我们实际选择逐步增长的N和µ用于CT，以平衡收敛速度和样本质量之间的权衡。

　　与扩散模型类似，一致性模型允许通过修改算法1中的多步采样过程来编辑零样本图像。我们使用一致性蒸馏在LSUN卧室数据集上训练的一致性模型演示了这种能力。在图6a中，我们展示了这样一个一致性模型可以在测试时对灰度卧室图像进行着色，即使它从未接受过着色任务的训练。在图6b中，我们展示了相同的一致性模型可以从生成高分辨率图像：

　　

6.1零样本图像编辑

　　采用算法4来实现图像的超分辨率。为简单起见，我们假设下采样图像是通过p*p大小的不重叠块获得的。假设全分辨率图像的形状为h*w*3。让y表示简单地向上采样到全分辨率的低分辨率图像，其中每个非重叠补丁中的像素共享相同的值。另外，设

为二进制掩码：

　　

　　超分辨率需要一个正交矩阵

，第一列是

该正交矩阵可通过QR分解得到。为了实现超分辨率，我们定义线性变换A:

　　

　　逆变换

：

　　

　　上述A和Ω的定义允许我们使用算法4进行图像超分辨率。