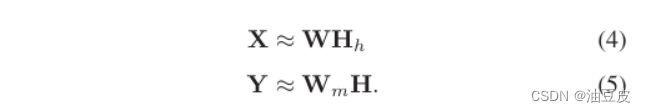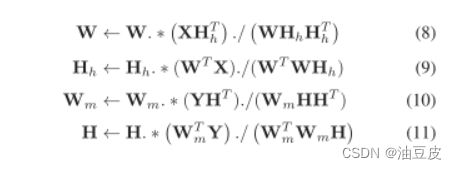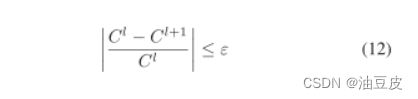用于高光谱和多光谱数据融合的耦合非负矩阵分解-解混合

论文：Coupled Nonnegative Matrix Factorization Unmixing
             for Hyperspectral and Multispectral Data Fusion

         摘要：本文提出了耦合非负矩阵分解解混合（CNMF），用于低空间分辨率高光谱和高空间分辨率多光谱数据的融合，以产生具有高空间和光谱分辨率的融合数据。

            CNMF算法将高光谱数据和多光谱数据交替地分解为端元矩阵和丰度矩阵。

          端元矩阵和丰度矩阵介绍

          在高光谱多光谱图像融合领域，"abundance matrices"（丰度矩阵）和 "endmember matrix"（端元矩阵）是两个重要的概念，涉及到图像融合和高光谱数据处理。

         1.Abundance Matrices（丰度矩阵）： 高光谱图像包含了大量的光谱波段信息，每个像素点都包含了一系列波段上的光谱反射率值。丰度矩阵是一个表示图像中各个像素点中不同成分（比如不同材料、物质）的成分丰度的矩阵。每个像素点的丰度向量表示该像素中不同成分的占比。通常情况下，高光谱图像可能包含多个光谱波段，因此丰度矩阵的每一行对应于一个像素，每一列对应于一个光谱波段。丰度矩阵的分析可以帮助识别图像中的不同物质成分。 想象一张图片，但不是彩色的，而是包含了很多种不同颜色的灰度。每个像素都代表了某种颜色的程度。在高光谱图像中，每个像素点的颜色（或者说光谱）是由许多不同的成分混合而成。丰度矩阵就像是告诉我们每个像素有多少来自不同成分的颜色。它是一个表格，每行代表一个像素，每列代表一种成分的颜色。通过分析丰度矩阵，我们可以了解哪些成分在图像中存在以及它们的占比。

        2.Endmember Matrix（端元矩阵）： 在高光谱图像中，每种地物或物质都具有独特的光谱特征，称为"端元"。端元矩阵是一个表示这些端元光谱的矩阵。通常，端元矩阵的每一列对应一个端元的光谱，而每一行对应不同的光谱波段。端元矩阵的提取和分析有助于确定高光谱图像中的不同物质或地物成分。想象你有一堆不同颜色的颜料，每个颜料都是某种独特颜色的代表。在高光谱图像中，每种地物或物质都有自己独特的光谱特征，就像是颜料的颜色。端元矩阵就是告诉我们不同地物或物质的光谱特征是什么样的。它也是一个表格，每列代表一种地物或物质，每行代表不同的光谱波段。通过分析端元矩阵，我们可以识别图像中的不同物质。

           总之，丰度矩阵帮助我们了解图像中不同成分的占比，而端元矩阵则帮助我们了解不同地物或物质的光谱特征。通过这些矩阵的分析，我们可以更好地理解图像的内容。

丰度矩阵（Abundance Matrix）和端元矩阵（Endmember Matrix）是在高光谱图像处理中使用的两个关键矩阵，它们之间存在一种重要的关系，用来描述图像中不同成分和它们的光谱特征。

            关系如下：

         丰度矩阵和端元矩阵的乘积： 在高光谱图像融合中，通过将丰度矩阵与端元矩阵相乘，可以重建出原始的高光谱图像。这个过程可以用一个简单的方程来表示：原始图像 = 丰度矩阵 × 端元矩阵。这意味着每个像素的光谱由丰度矩阵中的成分占比和端元矩阵中的光谱特征相乘得到。

         假设有一个高光谱图像，它包含了很多像素，每个像素有很多不同的光谱波段。我们用 A 来表示丰度矩阵，其中每个像素对应一个丰度向量，表示该像素中不同成分的占比。用 E 来表示端元矩阵，其中每列对应一个端元（地物或物质）的光谱特征。

       这样，原始的高光谱图像 X 可以用下面的方式表示：

                                        X=A×E

          其中，A 是丰度矩阵，E 是端元矩阵，X 是原始图像。矩阵相乘的结果表示通过不同端元的组合（用丰度矩阵中的占比来调节），可以重建出原始图像的光谱信息。

          这个关系反映了丰度矩阵和端元矩阵之间的相互作用：丰度矩阵指导如何用端元矩阵中的特征来构建出每个像素的光谱，从而帮助我们理解图像中不同地物或物质的分布和特征。

        CNMF算法：

         A:Sensor Observation Model(传感器观测模型)

         低空间分辨率高光谱数据的空间域与多光谱数据的空域相比有所退化。另一方面，多光谱数据是高空间分辨率高光谱数据的光谱退化形式。因此，X和Y被建模为：

                  

•          Z代表高空间分辨率高光谱数据，
•          X代表低空间分辨率高光谱数据，
•          Y代表高空间分辨率多光谱数据，
•          S代表空间扩展变换矩阵，每个列向量代表着点扩散函数（PSF）从多光谱图像到高光谱第k个像素值的变换。并且每一个PSF均被归一化。
•           R代表着光谱响应变换矩阵，每个行向量代表着从高光谱传感器到多光谱第i波段检测器的光谱响应函数的变换。
•           Es和Er是残差。
•           S由图像配准和PSF的估计来确定。R是通过辐射定标来获得光谱响应函数的

         B:Linear Spectral Mixture Model(线性光谱混合模型)

         假设每个像素处的光谱是几个端成员光谱的线性组合。因此，Z公式化为:

                          

•   W是谱特征矩阵，每个列向量表示端元谱，D表示段元数。
•   H是丰度矩阵，每个列向量表示像素处所有段元的丰度分数。
•   N是残差
  • 每个像素的丰度之和为1，即H的每个列向量之和为1

        注意：本论文中的 W,H矩阵的行，列向量的含义与博客前文介绍的端元矩阵和丰度矩阵介绍有出入大概意思一样，注意区分。

         通过将（3）代入（1）和（2），X和Y可以近似为

   

        定义空间退化的丰度矩阵Hh和谱退化的端元矩阵Wm，公式如下： 

       C:CNMF Unmixing(CNMF解混)

        基于解混的高光谱和多光谱数据融合是通过估计两个数据的高光谱分辨率端元光谱和高空间分辨率丰度图来实现的。

         CNMF通过NMF交替地对X和Y进行解混合，以估计W和H。

        本论文使用乘法更新规则进行NMF分解，其实就是NMF分解。规则如下：

                   

        CNMF算法从低空间分辨率高光谱数据的NMF解混开始。作为初始化阶段，我们通过顶点分量分析（VCA）设置端元数D 并计算初始端元矩阵W。

        Hh被设置为常数值1/D并且通过（9）被更新，直到与W的收敛被固定为止。

        作为优化阶段，通过（8）和（9）交替更新W和Hh，直到下一次收敛。

        X的下一轮NMF解混合与先前描述的第一轮的不同之处仅在于初始化阶段。Hh由（6）初始化，W由（8）更新，直到与Hh的收敛固定，以继承从多光谱数据获得的丰度图的可靠信息。

        下一步我们将NMF解混合应用于高空间分辨率的多光谱数据。

        作为初始化阶段，Wm由（7）设置。H被初始化为常数值1/D并且通过（11）被更新，直到与Wm的收敛被固定为止。

        这一过程对于继承从高光谱数据中获得的端元光谱的可靠信息非常重要（也就是第一步优化获取的W）

        作为优化阶段，通过（10）和（11）交替更新Wm和H，直到下一次收敛。

        交替地重复两个NMF解混合步骤，直到收敛。

        最后，我们可以通过将W乘以H来生成高空间分辨率的高光谱数据。

        我们将交替的NMF分解称为外循环，将每个NMF中的迭代更新称为内循环。作为收敛条件，我们使用成本函数C的变化率达到低于给定阈值ε的值的条件

                         

        其中l是迭代的索引。为了实用，迭代次数超过预定义的最大迭代次数的条件与收敛条件一起被添加到停止标准中。最大迭代次数被设置为内环和外环之间的不同值，分别称为Iin和Iout。