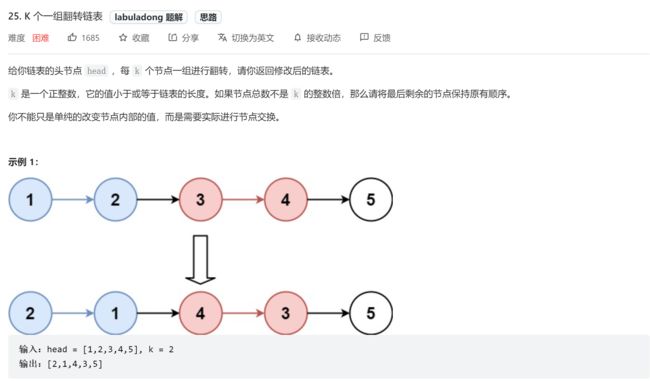
25.K个一组翻转链表
思路一 改变链表方向+分组反转
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
// 创建保护节点
ListNode protect = new ListNode(-1, head);
ListNode last = protect;
while(head != null) {
// 获取节点尾部
// 如果不满足条件, 比如 仅剩2个节点, 但是要返回3组, 就会直接返回null
ListNode tail = getTail(head, k);
// 边界问题 : tail = null , 最后一组不满足 k 个
if (tail == null) {
break;
}
// 记录尾部节点的下一个节点
ListNode nextNode = tail.next;
// 反转 head 到 tail 之间 n - 1 条边
reverse(head, tail);
// 上一组的尾部(未反转前的头部)指向当前组的头部(未反转前的尾部)
last.next = tail;
head.next = nextNode;
// 向后移动
last = head;
head = nextNode;
}
return protect.next;
}
public ListNode getTail(ListNode head, int k){
int walk = k - 1; // 实际要走的步数
if(walk <= 0) {
return head;
}
for(int i = 0; head != null && i < walk; i++ ) {
head = head.next;
}
return head;
}
private void reverse(ListNode head, ListNode tail){
if (head == tail) {
return;
}
// 这里注意, 我们不需要改变第一个节点的边的指向
// 所以原先 last = null => last = head , 向后移动一位
ListNode last = head;
head = head.next;
while(head != tail) {
ListNode nextNode = head.next;
// 改变边的方向
head.next = last;
// 指针向后移动
last = head;
head = nextNode;
}
// 注意 head 移动到 tail 位置时, 最后一条边的方向还未改变
tail.next = last;
}
}
基本思路如下 :
主体思路很简单, 分组去反转对应部分的链表, 然后再去考虑和当前组前面和后面节点的链接
首先我们要实现一个获取链表尾部的方法 :
- 传入
head和 链表的个数n返回链表的尾部
public ListNode getTail(ListNode head, int k){
int walk = k - 1; // 实际要走的步数
if(walk <= 0) {
return head;
}
for(int i = 0; head != null && i < walk; i++ ) {
head = head.next;
}
return head;
}
代码很简单, 但是要注意一些细节 :
- 我们要从head移动k步到尾部, 所以实际走的步数数 k - 1, 因为默认就在 head 上.
head != null这个条件, 当 最后一组的链表节点个数小于 k - 1的时候, 这个时候 还未循环结束, head 可能就走到了链表的末尾, 注意 : 此时 我们要返回的 tail 并不是链表的末尾, 而是 null
其次我们要将 链表的头部和尾部节点传入到 reverse 方法内去反转链表的边, 这个思路和 206.反转链表 的思路基本一致, 但是有一点不同
private void reverse(ListNode head, ListNode tail){
if (head == tail) {
return;
}
// 这里注意, 我们不需要改变第一个节点的边的指向
// 所以原先 last = null => last = head , 向后移动一位
ListNode last = head;
head = head.next;
while(head != tail) {
ListNode nextNode = head.next;
// 改变边的方向
head.next = last;
// 指针向后移动
last = head;
head = nextNode;
}
// 注意 head 移动到 tail 位置时, 最后一条边的方向还未改变
tail.next = last;
}
注意细节 :
反转链表时, 初始状态 last 是指向 null 的, 假如有5个节点, 我们实际上要反转 5条边, 包含开头指向null的边
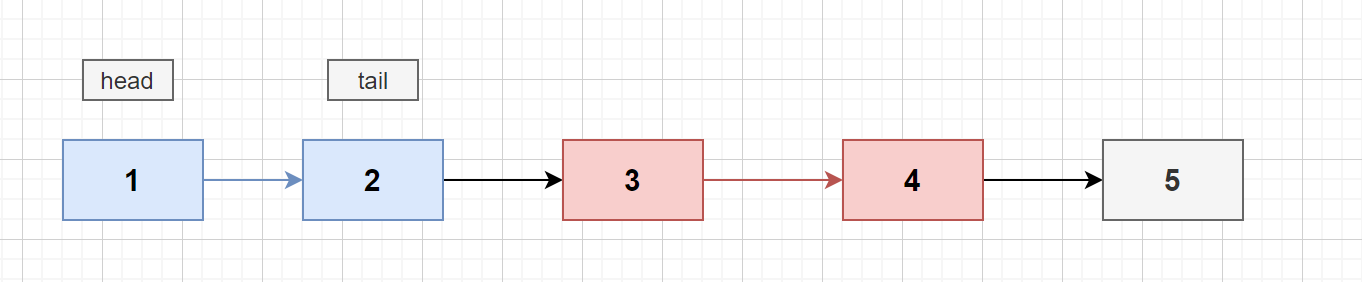
但是在这道题里面, 我们仅仅需要反转 n - 1 条边,如下图, 实际上我们要反转的是 节点 1 到 节点 2 的边即可
细节问题: 如果head和tial指向同一个节点, 我们就不需要反转边
if (head == tail) {
return;
}
然后, 我们需要把反转后的链表和其他节点连接, 另外需要注意的是, 我们考虑问题先考虑整体, 再考虑细节, 所以我们考虑中间的节点, 因为中间的节点不存在边界问题 :
public ListNode reverseKGroup(ListNode head, int k) {
// 创建保护节点
ListNode protect = new ListNode(-1, head);
ListNode last = protect;
while(head != null) {
// 获取节点尾部
// 如果不满足条件, 比如 仅剩2个节点, 但是要返回3组, 就会直接返回null
ListNode tail = getTail(head, k);
// 边界问题 : tail = null , 最后一组不满足 k 个
if (tail == null) {
break;
}
// 记录尾部节点的下一个节点
ListNode nextNode = tail.next;
// 反转 head 到 tail 之间 n - 1 条边
reverse(head, tail);
// 上一组的尾部(未反转前的头部)指向当前组的头部(未反转前的尾部)
last.next = tail;
head.next = nextNode;
// 向后移动
last = head;
head = nextNode;
}
return protect.next;
}
首先在反转链表之前需要记录尾部节点4的下一个节点5 : ListNode nextNode = tail.next; 因为反转以后, 节点 4 和 5之间的连接就断了
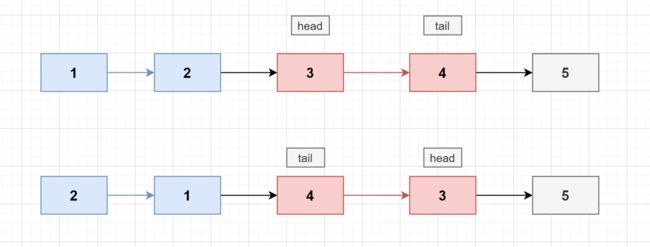
其次就是对链表进行反转, 然后将当前组和上一组的尾部与下一组的头部连接 :
- 前一组的尾部节点 1 指向反转后的头部节点 4 (未反转前的尾部节点) :
last.next = tail; - 当前组的尾部节点 3 (未反转前的头部节点) 指向 之前记录的节点 5
head.next = nextNode;
最后我们需要重新修改last节点指向当前组的尾部节点, 修改head节点指向下一组的头部节点
// 向后移动
last = head;
head = nextNode;
另外注意细节问题: 最后一组不满足k个的时候, 我们不需要反转, 所以当我们获取尾部以后 需要判断下
// 边界问题 : tail = null , 最后一组不满足 k 个
if (tail == null) {
break;
}
其次是保护节点 : 之所以要有保护节点的原因是, 我们考虑问题是考虑中间组的节点, 但是对于头结点来说, 它没有上一组的节点, 且无法获取 last (也就是上一组的尾结点) , 但是保护节点就可以很好的解决问题 :
初始时 last 直接指向 protect 节点即可, 头结点也不需要考虑边界问题.
完整代码如下 :
package cn.knightzz.leetcode.hard;
import cn.knightzz.link.ListNode;
import static cn.knightzz.link.utils.ListNodeUtils.*;
@SuppressWarnings("all")
public class LeetCode25 {
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
// 创建保护节点
ListNode protect = new ListNode(-1, head);
ListNode last = protect;
while(head != null) {
// 获取节点尾部
// 如果不满足条件, 比如 仅剩2个节点, 但是要返回3组, 就会直接返回null
ListNode tail = getTail(head, k);
// 边界问题 : tail = null , 最后一组不满足 k 个
if (tail == null) {
break;
}
// 记录尾部节点的下一个节点
ListNode nextNode = tail.next;
// 反转 head 到 tail 之间 n - 1 条边
reverse(head, tail);
// 上一组的尾部(未反转前的头部)指向当前组的头部(未反转前的尾部)
last.next = tail;
head.next = nextNode;
// 向后移动
last = head;
head = nextNode;
}
return protect.next;
}
public ListNode getTail(ListNode head, int k){
int walk = k - 1; // 实际要走的步数
if(walk <= 0) {
return head;
}
for(int i = 0; head != null && i < walk; i++ ) {
head = head.next;
}
return head;
}
private void reverse(ListNode head, ListNode tail){
if (head == tail) {
return;
}
// 这里注意, 我们不需要改变第一个节点的边的指向
// 所以原先 last = null => last = head , 向后移动一位
ListNode last = head;
head = head.next;
while(head != tail) {
ListNode nextNode = head.next;
// 改变边的方向
head.next = last;
// 指针向后移动
last = head;
head = nextNode;
}
// 注意 head 移动到 tail 位置时, 最后一条边的方向还未改变
tail.next = last;
}
}
}
思路二 计算链表长度+递归法反转
这个方法的思路很简单 : 先计算链表长度, 然后和 k 求余得到总共要反转多少组, 然后分组翻转即可
时间复杂度 O n O_{n} On
- 实现反转前n项的方法
reverseN(ListNode head, int n) - 实现反转第n到m个元素的方法 :
reverseBetwwen(ListNode head, int n , int m) - 计算链表长度, 然后通过求余得到反转的组数
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
int count = 1;
ListNode p = head;
while(p.next != null) {
p = p.next;
count++;
}
int nums = count / k;
int left = 1;
int right = k;
ListNode node = head;
for (int i = 0; i < nums; i++) {
node = reverseBetween(node, left, right);
left += k;
right+= k;
}
return node;
}
public ListNode reverseBetween(ListNode node, int left, int right) {
if (node == null || node.next == null || left >= right) {
return node;
}
int count = left;
// 创建虚拟头节点 [关键]
ListNode pre = new ListNode(-1, node);
ListNode p = pre;
while(count != 1) {
p = p.next;
count--;
}
ListNode head = reverseN(p.next,right - left + 1);
p.next = head;
return pre.next;
}
public ListNode reverseN(ListNode head, int n){
// 边界条件
if (n == 1) {
return head;
}
// 翻后转链表的头部
ListNode tail = reverseN(head.next, n - 1);
// 翻转链表的头部 , 注意 tail.next = null / 第 n + 1 个节点
ListNode p = head.next;
// 原因是 如果顺序反了, tail指向的目标会丢失
head.next = p.next;
p.next = head;
return tail;
}
}