机器学习 | 无监督聚类K-means和混合高斯模型
机器学习 | 无监督聚类K-means和混合高斯模型
1. 实验目的
实现一个K-means算法和混合高斯模型,并用EM算法估计模型中的参数。
2. 实验内容
用高斯分布产生 k k k个高斯分布的数据(不同均值和方差)(其中参数自己设定)。
-
用K-means聚类,测试效果;
-
用混合高斯模型和你实现的EM算法估计参数,看看每次迭代后似然值变化情况,考察EM算法是否可以获得正确的结果(与你设定的结果比较)。
-
可以UCI上找一个简单问题数据,用你实现的GMM进行聚类。
3. 实验环境
Windows11; Anaconda+python3.11; VS Code
4. 实验过程、结果及分析(包括代码截图、运行结果截图及必要的理论支撑等)
4.1 算法理论支撑
4.1.1 K-means聚类算法
K-means聚类算法的核心思想为假定聚类内部点之间的距离应该小于数据点与聚类外部的点之间的距离。即使得每个数据点和与它最近的中心之间距离的平方和最小。
假设数据集为 X = { x 1 , … , x N } , x i ∈ R D X = \left\{ x_{1},\ldots,x_{N} \right\},x_{i} \in \mathbb{R}^{D} X={x1,…,xN},xi∈RD,我们的目标是将数据集划分为 K K K个类别 Y Y Y。令 μ k ∈ R D , k = 1 , … , K \mu_{k} \in \mathbb{R}^{D},k = 1,\ldots,K μk∈RD,k=1,…,K表示各类别的中心。聚类问题等价于求概率分布:
P ( Y | X ) = P ( X | Y ) ∙ P ( Y ) P ( X ) P\left( Y \middle| X \right) = \frac{P\left( X \middle| Y \right) \bullet P(Y)}{P(X)} P(Y∣X)=P(X)P(X∣Y)∙P(Y)
K-means聚类相当于假设 P ( X | Y ) P\left( X \middle| Y \right) P(X∣Y)服从多元高斯分布(特征之间相互独立,协方差矩阵 Σ = λ I \Sigma\mathbf{=}\lambda\mathbf{I} Σ=λI),且 P ( Y ) P(Y) P(Y)为等概率均匀分布。而 P ( X ) P(X) P(X)为已知数据分布,从似然的角度看,极大化 P ( Y | X ) P\left( Y \middle| X \right) P(Y∣X)即等价于极大化 P ( X | Y ) ∼ − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) P\left( X \middle| Y \right)\sim - \frac{1}{2}(x - \mu)^{T}\Sigma^{- 1}(x - \mu) P(X∣Y)∼−21(x−μ)TΣ−1(x−μ),即最小化各数据点到其类别的均值。
多元正态分布: N ( x ∣ μ , Σ ) = 1 ( 2 π ) D / 2 1 ∣ Σ ∣ 1 / 2 exp { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } 多元正态分布:\mathcal{N(}x|\mu,\Sigma) = \frac{1}{(2\pi)^{D/2}}\frac{1}{\mid \Sigma \mid^{1/2\ }}\exp\{ - \frac{1}{2}(x - \mu)^{T}\Sigma^{- 1}(x - \mu)\}\ 多元正态分布:N(x∣μ,Σ)=(2π)D/21∣Σ∣1/2 1exp{−21(x−μ)TΣ−1(x−μ)}
引入二值指示变量 r n k ∈ { 0 , 1 } r_{nk} \in \{ 0,1\} rnk∈{0,1}表示数据点的分类情况,则可定义目标函数为
min r , μ J = ∑ n = 1 N ∑ k = 1 K r n k ∥ x n − μ k ∥ 2 \min_{r,\mu}{J = \sum_{n = 1}^{N}{\sum_{k = 1}^{K}{r_{nk}\left\| x_{n} - \mu_{k} \right\|^{2}}}} r,μminJ=n=1∑Nk=1∑Krnk∥xn−μk∥2
因此最优化过程可以划分为两步:
- 固定 μ \mu μ,优化 r n k r_{nk} rnk。由于 J J J关于 r n k r_{nk} rnk是线性的,因此可以对每个 n n n分别进行最小化,即对 r n k r_{nk} rnk根据与聚类中心的距离进行最优化:
r n k = { 1 , k = a r g m i n j ∥ x n − μ j ∥ 2 0 , 其他情况 r_{nk} = \left\{ \begin{aligned} 1 ,&\ \ \ \ \ \ \ \ \ k = argmin_{j}\left\| x_{n} - \mu_{j} \right\|^{2} \\ 0 ,&\ \ \ \ \ \ \ \ \ 其他情况\ \ \ \end{aligned} \right.\ rnk={1,0, k=argminj∥xn−μj∥2 其他情况
- 固定 r n k r_{nk} rnk,优化 μ \mu μ。由于 J J J是 μ \mu μ的二次函数,对其求导等于零得
∂ J ∂ μ k = 2 ∑ n = 1 N r n k ( x n − μ k ) = 0 ⇒ μ k = ∑ n r n k x n ∑ n r n k \frac{\partial J}{\partial\mu_{k}} = 2\sum_{n = 1}^{N}{r_{nk}(x_{n} - \mu_{k}) = 0} \Rightarrow \mu_{k} = \frac{\sum_{n}^{}{r_{nk}x_{n}}}{\sum_{n}^{}r_{nk}} ∂μk∂J=2n=1∑Nrnk(xn−μk)=0⇒μk=∑nrnk∑nrnkxn
即 μ k \mu_{k} μk等于类别k的所有数据点的均值。
4.1.2 混合高斯模型
任意连续概率密度都能用多个高斯分布的线性组合叠加的高斯混合概率分布 p ( x ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) p(x) = \sum_{k = 1}^{K}{\pi_{k}\mathcal{N}(x|\mu_{k},\Sigma_{k})} p(x)=∑k=1KπkN(x∣μk,Σk)来描述。引入 " 1 o f K " "1\ of\ K" "1 of K"编码的二值随机变量 z \mathcal{z} z,满足 z k ∈ { 0 , 1 } \mathcal{z}_{k} \in \{ 0,1\} zk∈{0,1}且 ∑ k = 1 K z k = 1 \sum_{k = 1}^{K}\mathcal{z}_{k} = 1 ∑k=1Kzk=1。
由右图模型定义联合概率分布 p ( x , z ) = p ( z ) ∙ p ( x ∣ z ) p\left( x,\mathcal{z} \right) = p\mathcal{(z) \bullet}p\left( x|\mathcal{z} \right) p(x,z)=p(z)∙p(x∣z), z \mathcal{z} z的边缘先验概率分布设为 p ( z k = 1 ) = π k ( 0 ≤ π k ≤ 1 且 ∑ k = 1 K π k = 1 ) p(\mathcal{z}_{k} = 1) = \pi_{k}(0 \leq \pi_{k} \leq 1且\sum_{k = 1}^{K}{\pi_{k} = 1}) p(zk=1)=πk(0≤πk≤1且∑k=1Kπk=1),也可写作 p ( z ) = ∏ k = 1 K π k z k p(\mathcal{z}) = \prod_{k = 1}^{K}\pi_{k}^{\mathcal{z}_{k}} p(z)=∏k=1Kπkzk。
那么, x x x的条件概率分布为:
p ( x ∣ z k = 1 ) = N ( x ∣ μ k , Σ k ) ⇔ p ( x ∣ z ) = ∏ k = 1 K N ( x ∣ μ k , Σ k ) z k p(x|\mathcal{z}_{k} = 1) = \mathcal{N(}x|\mu_{k},\Sigma_{k}) \Leftrightarrow \ p(x|\mathcal{z}) = \prod_{k = 1}^{K}{\mathcal{N(}x|\mu_{k},\Sigma_{k})^{\mathcal{z}_{k}}} p(x∣zk=1)=N(x∣μk,Σk)⇔ p(x∣z)=k=1∏KN(x∣μk,Σk)zk
于是可以给出 p ( x ) = ∑ z p ( z ) ∙ p ( x ∣ z ) = ∑ k = 1 K π k N ( x ∣ μ k , Σ k ) p(x) = \sum_{\mathcal{z}}^{}{p\mathcal{(z) \bullet}p\left( x\mathcal{|z} \right)} = \sum_{k = 1}^{K}{\pi_{k}\mathcal{N(}x|\mu_{k},\Sigma_{k})} p(x)=∑zp(z)∙p(x∣z)=∑k=1KπkN(x∣μk,Σk),同时, z \mathcal{z} z的条件后验概率 γ ( z k ) \gamma(\mathcal{z}_{k}) γ(zk)由贝叶斯定理得(已知为 x x x,类别为 z k \mathcal{z}_{k} zk的概率):
γ ( z k ) ≡ p ( z k = 1 | x ) = p ( z k = 1 ) p ( x | z k = 1 ) ∑ j = 1 K p ( z j = 1 ) p ( x ∣ z j = 1 ) = π k N ( x ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x ∣ μ j , Σ k ) \begin{array}{r} \gamma(z_{k}) \equiv p\left( \mathcal{z}_{k} = 1 \middle| x \right) \end{array} = \frac{p\left( z_{k} = 1 \right)p\left( x \middle| z_{k} = 1 \right)}{\sum_{j = 1}^{K}{p\left( z_{j} = 1 \right)p\left( x\mid z_{j} = 1 \right)}}\ = \frac{\pi_{k}\mathcal{N}\left( x\mid\mu_{k},\Sigma_{k} \right)}{\sum_{j = 1}^{K}{\pi_{j}\mathcal{N}\left( x\mid\mu_{j},\Sigma_{k} \right)}} γ(zk)≡p(zk=1∣x)=∑j=1Kp(zj=1)p(x∣zj=1)p(zk=1)p(x∣zk=1) =∑j=1KπjN(x∣μj,Σk)πkN(x∣μk,Σk)
于是此聚类过程可以看做将概率分布 p ( x ) p(x) p(x)解耦成 K K K个高斯分布,对应 K K K个类别。对于数据集 X = { x 1 , … , x N } , x i ∈ R D , X ∈ R N × D X = \left\{ x_{1},\ldots,x_{N} \right\},x_{i} \in \mathbb{R}^{D},X \in \mathbb{R}^{N \times D} X={x1,…,xN},xi∈RD,X∈RN×D,对应隐变量表示为 Z ∈ R N × K Z \in \mathbb{R}^{N \times K} Z∈RN×K。
则对数似然函数为
ln p ( X ∣ π , μ , Σ ) = ∑ n = 1 N ln { ∑ k = 1 K π k N ( x n ∣ μ k , Σ k ) } \ln p(X \mid \pi,\mu,\Sigma) = \sum_{n = 1}^{N}{\ln\left\{ \sum_{k = 1}^{K}{\pi_{k}\mathcal{N}\left( x_{n}\mid\mu_{k},\Sigma_{k} \right)} \right\}} lnp(X∣π,μ,Σ)=n=1∑Nln{k=1∑KπkN(xn∣μk,Σk)}
将此似然函数关于 μ k \mu_{k} μk求导(假设 Σ k \Sigma_{k} Σk非奇异),令 N k = ∑ n = 1 N γ ( z n k ) , γ ( z n k ) ≡ p ( z k = 1 | x n ) N_{k} = \sum_{n = 1}^{N}{\gamma\left( z_{nk} \right),\ \gamma\left( z_{nk} \right) \equiv p\left( z_{k} = 1 \middle| x_{n} \right)} Nk=∑n=1Nγ(znk), γ(znk)≡p(zk=1∣xn)为能被分配到聚类 k k k的有效数量,可以得到:
∑ n = 1 K π k N ( x n ∣ μ k , Σ k ) ∑ j π j N ( x n ∣ μ j , Σ j ) ⏟ γ ( z n k ) Σ k − 1 ( x n − μ k ) = 0 ⇒ μ k = 1 N k ∑ n = 1 N γ ( z n k ) x n \sum_{n=1}^{K}\frac{\pi_{k}\mathcal{N}(x_{n}\mid\mu_{k},\Sigma_{k})}{\underbrace{\sum_{j}\pi_{j}\mathcal{N}(x_{n}\mid\mu_{j},\Sigma_{j})}_{\gamma({z}_{nk})}}\Sigma_{k}^{-1}(x_{n}-\mu_{k})=0\Rightarrow\mu_{k}=\frac{1}{N_{k}}\sum_{n=1}^{N}\gamma(z_{nk})x_{n} n=1∑Kγ(znk) j∑πjN(xn∣μj,Σj)πkN(xn∣μk,Σk)Σk−1(xn−μk)=0⇒μk=Nk1n=1∑Nγ(znk)xn
由此式 μ k \mu_{k} μk可视为当前所有点数据为第 k k k类的概率加权平均。
同样地,将此函数关于 Σ k \Sigma_{k} Σk求导等于0可以得到:
Σ k = 1 N k ∑ n = 1 N γ ( z n k ) ( x n − μ k ) ( x − μ k ) T \Sigma_{k} = \frac{1}{N_{k}}\sum_{n = 1}^{N}{\gamma(z_{nk})(x_{n} - \mu_{k})(x - \mu_{k})^{T}} Σk=Nk1n=1∑Nγ(znk)(xn−μk)(x−μk)T
最后使用拉格朗日乘子法关于 π k \pi_{k} πk优化 ln p ( X ∣ π , μ , Σ ) + λ ( ∑ k = 1 K π k − 1 ) \ln{p\left( X\mid\pi,\mu,\Sigma \right)} + \lambda(\sum_{k = 1}^{K}{\pi_{k} - 1}) lnp(X∣π,μ,Σ)+λ(∑k=1Kπk−1)( π k \pi_{k} πk需要满足和为1的条件)得到:
∑ n = 1 N N ( x n ∣ μ k , Σ k ) ∑ j π j N ( x n ∣ μ j , Σ j ) + λ = 0 ⇒ π k = N k N \sum_{n = 1}^{N}{\frac{\mathcal{N(}x_{n} \mid \mu_{k},\Sigma_{k})}{\sum_{j}^{}{\pi_{j}\mathcal{N(}x_{n} \mid \mu_{j},\Sigma_{j})}} + \lambda} = 0 \Rightarrow \pi_{k} = \frac{N_{k}}{N} n=1∑N∑jπjN(xn∣μj,Σj)N(xn∣μk,Σk)+λ=0⇒πk=NNk
使用EM算法优化 ln p ( X ∣ π , μ , Σ ) \ln p(X \mid \pi,\mu,\Sigma) lnp(X∣π,μ,Σ)即可总结为以下步骤:
ALGORITHM 1 EM for Gaussian Mixture Models
- input X ← X \leftarrow X←数据集, K ← K \leftarrow K←类别数目, i t e r ← iter \leftarrow iter←迭代次数;
- 初始化均值 μ k \mu_{k} μk、协方差 Σ k \Sigma_{k} Σk和混合系数 π k \pi_{k} πk
- 计算对数似然 ln p ( X ∣ π , μ , Σ ) ← ∑ n = 1 N ln { ∑ k = 1 K π k N ( x n ∣ μ k , Σ k ) } \ln p(X \mid \pi,\mu,\Sigma) \leftarrow \sum_{n = 1}^{N}{\ln\left\{ \sum_{k = 1}^{K}{\pi_{k}\mathcal{N}\left( x_{n}\mid\mu_{k},\Sigma_{k} \right)} \right\}} lnp(X∣π,μ,Σ)←∑n=1Nln{∑k=1KπkN(xn∣μk,Σk)}
- while i < i t e r i < iter i<iter do
- γ ( z n k ) ← π k N ( x n ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x n ∣ μ j , Σ j ) \gamma(z_{nk}) \leftarrow \frac{\pi_{k}\mathcal{N}\left( x_{n}\mid\mu_{k},\Sigma_{k} \right)}{\sum_{j = 1}^{K}{\pi_{j}\mathcal{N}\left( x_{n}\mid\mu_{j},\Sigma_{j} \right)}} γ(znk)←∑j=1KπjN(xn∣μj,Σj)πkN(xn∣μk,Σk); (E步)
- μ k n e w ← 1 N k ∑ n = 1 N γ ( z n k ) x n \mu_{k}^{new} \leftarrow \frac{1}{N_{k}}\sum_{n = 1}^{N}{\gamma(z_{nk})x_{n}} μknew←Nk1∑n=1Nγ(znk)xn;
- Σ k n e w ← 1 N k ∑ n = 1 N γ ( z n k ) ( x n − μ k n e w ) ( x − μ k n e w ) T \Sigma_{k}^{new} \leftarrow \frac{1}{N_{k}}\sum_{n = 1}^{N}{\gamma(z_{nk})(x_{n} - \mu_{k}^{new})(x - \mu_{k}^{new})^{T}} Σknew←Nk1∑n=1Nγ(znk)(xn−μknew)(x−μknew)T; (M步)
- π k n e w ← N k N \pi_{k}^{new} \leftarrow \frac{N_{k}}{N} πknew←NNk;
- end while
- return μ k , Σ k , π k \mu_{k},\Sigma_{k},\pi_{k} μk,Σk,πk //返回最优参数;
4.2 实验设计
4.2.1 随机数据生成
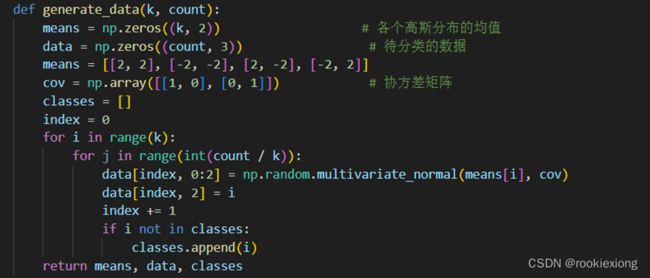
如上图代码,使用np.random.multivariate_normal方法按给定的协方差矩阵和均值按多元高斯分布初始化 k k k个类别的数据点。
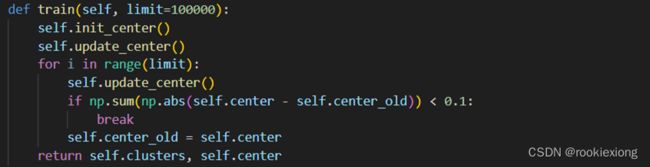
4.2.2 K-means聚类
首先初始化 k k k个类的中心,这里采取的是从数据集中随机选取 k k k个样本作为初始的 k k k类中心。
而后是更新中心的算法,主要是分为两步:
-
通过计算每个样本到 k k k个中心的距离(欧式距离),然后选取最小的距离对应的那个聚类中心作为样本标签,将该样本划分到这个类中,
-
根据更新后的类别计算类内均值,作为新的中心。
重复上述过程,直至中心更新距离较之上次变化较小时退出迭代。
4.2.3 混合高斯模型GMM
首先初始化 k k k个类的均值、协方差和混合系数,可以有随机生成和采用K-means聚类的结果两种方式进行初始化。
根据对数似然计算公式 l n p ( X ∣ π , μ , Σ ) ← ∑ n = 1 N ln { ∑ k = 1 K π k N ( x n ∣ μ k , Σ k ) } lnp(X \mid \pi,\mu,\Sigma) \leftarrow \sum_{n = 1}^{N}{\ln\left\{ \sum_{k = 1}^{K}{\pi_{k}\mathcal{N}\left( x_{n}\mid\mu_{k},\Sigma_{k} \right)} \right\}} lnp(X∣π,μ,Σ)←∑n=1Nln{∑k=1KπkN(xn∣μk,Σk)}以及 关于 μ k \mu_{k} μk、 Σ k \Sigma_{k} Σk和 π k \pi_{k} πk的导数进行EM更新:
-
E步:计算 γ ( z n k ) ← π k N ( x n ∣ μ k , Σ k ) ∑ j = 1 K π j N ( x n ∣ μ j , Σ j ) \gamma(z_{nk}) \leftarrow \frac{\pi_{k}\mathcal{N}\left( x_{n}\mid\mu_{k},\Sigma_{k} \right)}{\sum_{j = 1}^{K}{\pi_{j}\mathcal{N}\left( x_{n}\mid\mu_{j},\Sigma_{j} \right)}} γ(znk)←∑j=1KπjN(xn∣μj,Σj)πkN(xn∣μk,Σk),即各数据点的类别概率;
-
M步:计算新的均值 μ k n e w = 1 N k ∑ n = 1 N γ ( z n k ) x n , 混合系数 π k n e w ← N k N 以及 协方差 Σ k n e w = 1 N k ∑ n = 1 N γ ( z n k ) ( x n − μ k n e w ) ( x − μ k n e w ) T \mu_{k}^{new} = \frac{1}{N_{k}}\sum_{n = 1}^{N}{\gamma(z_{nk})x_{n}},\ 混合系数\pi_{k}^{new} \leftarrow \frac{N_{k}}{N}以及{协方差\Sigma}_{k}^{new} = \frac{1}{N_{k}}\sum_{n = 1}^{N}{\gamma(z_{nk})(x_{n} - \mu_{k}^{new})(x - \mu_{k}^{new})^{T}} μknew=Nk1∑n=1Nγ(znk)xn, 混合系数πknew←NNk以及协方差Σknew=Nk1∑n=1Nγ(znk)(xn−μknew)(x−μknew)T
重复上述过程,直至似然函数较之上次变化较小时退出迭代。
4.3 实验结果及分析
4.3.1 自己生成数据结果比较
设置均值为 ( − 2 , − 2 ) , ( 2 , − 2 ) , ( 2 , 2 ) , ( − 2 , 2 ) ( - 2, - 2),(2, - 2),(2,2),( - 2,2) (−2,−2),(2,−2),(2,2),(−2,2),协方差矩阵均为 [ 1 0 0 1 ] \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} [1001],生成1000组数据,而后先后使用K-means和GMM进行聚类,聚类结果如下:
K-means正确率为96.7%,GMM正确率为96.9%(在使用K-means的结果作为GMM初始化的条件下)。
同时,经过反复实验发现,K-means和GMM的聚类结果严重依赖于初始化的结果,当初始化中心(或均值)选取区分度不高时,结果往往会比较差。
而GMM以K-means的结果初始化,能够一定程度上优化K-means的聚类结果(特别是当分类结果不好时)。

而特征之间不相互独立时,GMM聚类结果明显优于K-means。这是由于K-means假设数据呈球状分布,不能够区分开具有不相互独立的特征。
下图为均值为 ( − 2 , − 2 ) , ( 2 , − 2 ) , ( 2 , 2 ) , ( − 2 , 2 ) ( - 2, - 2),(2, - 2),(2,2),( - 2,2) (−2,−2),(2,−2),(2,2),(−2,2),协方差矩阵均为 [ 1 0.36 0.36 1 ] \begin{bmatrix} 1 & 0.36 \\ 0.36 & 1 \end{bmatrix} [10.360.361],生成1000组数据,先后使用K-means和GMM进行聚类的聚类结果如下:
此时K-means正确率为91.8%,GMM正确率为97.6%。
4.3.2 UCI-Iris数据集结果比较
而后使用Iris数据集进行聚类,K-means分类正确率为88%,GMM的分类正确率为96.7%,将聚类结果按第一个特征和第二个特征进行可视化结果如下:
5. 实验结论
K-means和GMM都是EM算法的体现。两者共同之处都有隐变量,遵循EM算法的E步和M步的迭代优化。
K-means其实就是一种特殊的高斯混合模型,提出了强假设,假设每一类在样本数据中出现的概率相等均为 1 k \frac{1}{k} k1,每个特征间相互独立,且满足变量间的协方差矩阵为单位对角阵。在此条件下,可以直接用欧氏距离作为K-means的协方差去衡量相似性。
而GMM用混合高斯模型来描述聚类结果,且假设多个高斯模型对总模型的贡献是有权重的,且样本属于某一类也是由概率的,从而相似度也由离散的 0 , 1 0,1 0,1变成了需要通过全概率公式计算的值,分类效果一般好于K-means。
实验发现,初值的选取对K-means和GMM的效果影响较大,初始化较差可能会导致陷入局部最优解而得不到较好的聚类结果。可以使用GMM对K-means的分类结果进行进一步优化。
6. 参考文献
[1]李航. 统计学习方法[M]. 清华大学出版社, 2012.
[2]周志华. 机器学习[M]. 清华大学出版社, 2016.
[3]Bishop C .Pattern Recognition and Machine Learning[M]. 2006.