Atcoder Beginner Contest 336 （A - F 题）

A - Long Loong

Problem Statement

For a positive integer $X$, the Dragon String of level $X$ is a string of length $(X+3)$ formed by one L, $X$ occurrences of o, one n, and one g arranged in this order.
You are given a positive integer $N$. Print the Dragon String of level $N$.

Note that uppercase and lowercase letters are distinguished.

Constraints

$1\le N\le 2024$
$N$ is an integer.

Input

The input is given from Standard Input in the following format:
$N$

Output

Print the Dragon String of level $N$.

Sample Input 1

3

Sample Output 1

Looong

Arranging one L, three os, one n, and one g in this order yields Looong.

Sample Input 2

1

Sample Output 2

Long

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int X;

	cin >> X;

	cout << 'L';
	for (int i = 1; i <= X; i ++)
		cout << 'o';
	cout << "ng";

	return 0;
}

B - CTZ

Problem Statement

For a positive integer $X$, let $\text{ctz}(X)$ be the (maximal) number of consecutive zeros at the end of the binary notation of $X$.

If the binary notation of $X$ ends with a $1$, then $\text{ctz}(X)=0$.
You are given a positive integer $N$. Print $\text{ctz}(N)$.

Constraints

$1\le N\le 10^9$
$N$ is an integer.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print $\text{ctz}(N)$.

Sample Input 1

2024

Sample Output 1

3

$2024$ is 11111101000 in binary, with three consecutive 0s from the end, so $\text{ctz}(2024)=3$.

Thus, print $3$.

Sample Input 2

18

Sample Output 2

1

$18$ is 10010 in binary, so $\text{ctz}(18)=1$.

Note that we count the trailing zeros.

Sample Input 3

5

Sample Output 3

0

Solution

具体见文后视频。

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int N;

	cin >> N;

	int Result = 0;
	for (int i = 0; i <= 32; i ++)
		if (!(N >> i & 1))
			Result ++;
		else
			break;

	cout << Result << endl;

	return 0;
}

C - Even Digits

Problem Statement

A non-negative integer $n$ is called a good integer when it satisfies the following condition:
All digits in the decimal notation of $n$ are even numbers ($0$, $2$, $4$, $6$, and $8$).
For example, $0$, $68$, and $2024$ are good integers.
You are given an integer $N$. Find the $N$-th smallest good integer.

Constraints

$1\le N\le 10^{12}$
$N$ is an integer.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print the $N$-th smallest good integer.

Sample Input 1

8

Sample Output 1

24

The good integers in ascending order are $0,2,4,6,8,20,22,24,26,28,\dots$.

The eighth smallest is $24$, which should be printed.

Sample Input 2

133

Sample Output 2

2024

Sample Input 3

31415926535

Sample Output 3

2006628868244228

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

int A[7] = {0, 0, 2, 4, 6, 8};

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int N;

	cin >> N;

	if (N == 1)
	{
		cout << 0 << endl;
		return 0;
	}

	std::vector<int> Num;
	while (N != 1)
	{
		int V = N % 5;
		if (!V) V = 5;
		Num.push_back(A[V]), N = (N + 4) / 5;
	}

	reverse(Num.begin(), Num.end());

	for (auto c : Num)
		cout << c;

	return 0;
}

D - Pyramid

Problem Statement

For a positive integer $k$, the Pyramid Sequence of size $k$ is a sequence of length $(2k-1)$ where the terms of the sequence have the values $1,2,\dots ,k-1,k,k-1,\dots ,2,1$ in this order.
You are given a sequence $A=(A_1,A_2,\dots ,A_N)$ of length $N$.

Find the maximum size of a Pyramid Sequence that can be obtained by repeatedly choosing and performing one of the following operations on $A$ (possibly zero times).
Choose one term of the sequence and decrease its value by $1$.
Remove the first or last term.
It can be proved that the constraints of the problem guarantee that at least one Pyramid Sequence can be obtained by repeating the operations.

Constraints

$1\le N\le 2\times 10^5$
$1\le A_i\le 10^9$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$
$A_1$ $A_2$ $\dots$ $A_N$

Output

Print the maximum size of the Pyramid Sequence that can be obtained by repeatedly performing the operations described in the problem statement on the sequence $A$.

Sample Input 1

5
2 2 3 1 1

Sample Output 1

2

Starting with $A=(2,2,3,1,1)$, you can create a Pyramid Sequence of size $2$ as follows:
Choose the third term and decrease it by $1$. The sequence becomes $A=(2,2,2,1,1)$.
Remove the first term. The sequence becomes $A=(2,2,1,1)$.
Remove the last term. The sequence becomes $A=(2,2,1)$.
Choose the first term and decrease it by $1$. The sequence becomes $A=(1,2,1)$.
$(1,2,1)$ is a Pyramid Sequence of size $2$.

On the other hand, there is no way to perform the operations to create a Pyramid Sequence of size $3$ or larger, so you should print $2$.

Sample Input 2

5
1 2 3 4 5

Sample Output 2

3

Sample Input 3

1
1000000000

Sample Output 3

1

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 2e5 + 10;

int N;
int A[SIZE];
int Pre[SIZE], Suf[SIZE];

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N;

	for (int i = 1; i <= N; i ++)
		cin >> A[i];

	for (int i = 1, j = 1; i <= N; i ++)
	{
		while (A[j] >= j - i + 1 && j <= N) j ++;
		Pre[i] = j - 1;
	}
	for (int i = N, j = N; i >= 1; i --)
	{
		while (A[j] >= i - j + 1 && j >= 1) j --;
		Suf[i] = j + 1;
	}

	int Result = 0;
	for (int i = 1; i <= N; i ++)
	{
		int l = 0, r = min(i - 1, N - i);
		while (l < r)
		{
			int mid = l + r + 1 >> 1;
			if (Pre[i - mid] >= i && Suf[i + mid] <= i) l = mid;
			else r = mid - 1;
		}
		Result = max(Result, r + 1);
	}

	cout << Result << endl;

	return 0;
}

E - Digit Sum Divisible

Problem Statement

The digit sum of a positive integer $n$ is defined as the sum of the digits in the decimal notation of $n$. For example, the digit sum of $2024$ is $2+0+2+4=8$.

A positive integer $n$ is called a good integer when $n$ is divisible by its digit sum. For example, $2024$ is a good integer because it is divisible by its digit sum of $8$.

You are given a positive integer $N$. How many good integers are less than or equal to $N$?

Constraints

$1\le N\le 10^{14}$
$N$ is an integer.

Input

The input is given from Standard Input in the following format:

$N$

Output

Print the number of good integers less than or equal to $N$.

Sample Input 1

20

Sample Output 1

13

There are $13$ good integers less than or equal to $20$: $1,2,3,4,5,6,7,8,9,10,12,18,20$.

Sample Input 2

2024

Sample Output 2

409

Sample Input 3

9876543210

Sample Output 3

547452239

Solution

具体见文后视频。

---

Code

#include 
#include 
#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 2e2 + 10;

int F[20][SIZE][SIZE];
std::vector<int> A;

int DP(int Limit, int Pos, int Cur, int Mod, int Sum)
{
	if (Cur > Sum) return 0;
	if (!Pos) return (Mod == 0 && Cur == Sum);
	if (!Limit && ~F[Pos][Cur][Mod]) return F[Pos][Cur][Mod];

	int Max = (Limit ? A[Pos - 1] : 9), Result = 0;
	for (int i = 0; i <= Max; i ++)
		Result += DP(Limit && (i == Max), Pos - 1, Cur + i, (Mod * 10 + i) % Sum, Sum);

	if (!Limit) F[Pos][Cur][Mod] = Result;
	return Result;
}

int Work(int N)
{
	A.clear();
	while (N) A.push_back(N % 10), N /= 10;

	int M = A.size(), Result = 0;
	for (int i = 1; i <= M * 9; i ++)
	{
		memset(F, -1, sizeof F);
		Result += DP(1, M, 0, 0, i);
	}

	return Result;
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int N;

	cin >> N;

	cout << Work(N) << endl;

	return 0;
}

F - Rotation Puzzle

Problem Statement

There is a grid with $H$ rows and $W$ columns. Initially, each integer from $1$ to $(H\times W)$ is written exactly once in the grid.

Specifically, for $1\le i\le H$ and $1\le j\le W$, the cell at the $i$-th row from the top and the $j$-th column from the left contains $S_{i,j}$.

Below, let $(i,j)$ denote the cell at the $i$-th row from the top and the $j$-th column from the left.
Determine if it is possible to reach a state where, for all pairs of integers $(i,j)$ $(1\le i\le H,1\le j\le W)$,

the cell $(i,j)$ contains the integer $((i-1)\times W+j)$ by repeating the following operation at most $20$ times (possibly zero).

If it is possible, print the minimum number of operations required.

If it is impossible in $20$ or fewer operations (including the case where it is impossible no matter how many times the operation is repeated), print $-1$.

Operation: Choose a rectangle of size $(H-1) \times (W-1)$ from the grid and rotate it $180$ degrees.
More precisely, choose integers $x$ and $y$ $(0 \leq x, y \leq 1)$,
and for all pairs of integers $(i,j)$ satisfying $1 \leq i \leq H-1$ and $1 \leq j \leq W-1$,
simultaneously replace the integer written in cell $(i+x,j+y)$ with the number written in cell $(H-i+x,W-j+y)$.

Note that it is only necessary for the integers written in the cells to satisfy the condition; the orientation in which they are written does not matter. ## Constraints

$3\le H,W\le 8$
$1\le S_{i,j}\le H\times W$
If $(i,j)\ne (i^{\prime },j^{\prime })$, then $S_{i,j}\ne S_{i^{\prime },j^{\prime }}$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$H$ $W$
$S_{1,1}$ $S_{1,2}$ $\dots$ $S_{1,W}$
$S_{2,1}$ $S_{2,2}$ $\dots$ $S_{2,W}$
$⋮$
$S_{H,1}$ $S_{H,2}$ $\dots$ $S_{H,W}$

Output

Print the minimum number of operations required to meet the conditions of the problem statement.

If it is impossible to satisfy the conditions with $20$ or fewer operations, output $-1$.

Sample Input 1

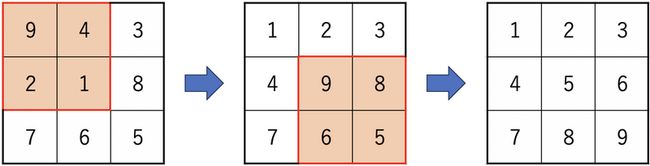
3 3
9 4 3
2 1 8
7 6 5

Sample Output 1

2

Operating in the following order will satisfy the conditions of the problem statement in $2$ operations.
Operate by choosing the rectangle in the top-left corner. That is, by choosing $x=0$ and $y=0$.
Operate by choosing the rectangle in the bottom-right corner. That is, by choosing $x=1$ and $y=1$.
On the other hand, it is impossible to satisfy the conditions with one or fewer operations, so print $2$.

Sample Input 2

4 6
15 18 1 14 3 4
23 24 19 8 9 12
13 2 17 6 5 16
21 22 7 20 11 10

Sample Output 2

-1

It is impossible to satisfy the conditions with $20$ or fewer operations, so print $-1$.

Sample Input 3

4 6
1 4 13 16 15 18
21 20 9 12 23 10
17 14 5 6 3 2
11 22 7 24 19 8

Sample Output 3

20

Sample Input 4

4 3
1 2 3
4 5 6
7 8 9
10 11 12

Sample Output 4

0

Solution

具体见文后视频。

---

Code

#include 
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int SIZE = 10;

int H, W;
int A[SIZE][SIZE];
unordered_map<string, int> D[2];

int Id(int X, int Y) { return (X - 1) * W + Y; }

void BFS(string S, int k)
{
	queue<string> Q;
	D[k][S] = 0;
	Q.push(S);

	while (Q.size())
	{
		auto T = Q.front();
		Q.pop();

		// cout << T << ":" << D[k][T] << " " << D[k].count(" 123456789") << endl;
		if (D[k][T] >= 10) break;

		for (int X = 0; X <= 1; X ++)
			for (int Y = 0; Y <= 1; Y ++)
			{
				string Source = T;
				for (int i = 1; i < H; i ++)
					for (int j = 1; j < W; j ++)
						Source[Id(i + X, j + Y)] = T[Id(H - i + X, W - j + Y)];
				if (!D[k].count(Source))
				{
					D[k][Source] = D[k][T] + 1;
					Q.push(Source);
				}
			}
	}
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> H >> W;

	string S1 = " ", S2 = " ";
	for (int i = 1, k = 1; i <= H; i ++)
		for (int j = 1; j <= W; j ++, k ++)
			cin >> A[i][j], S1 += char(A[i][j] + '0'), S2 += char(k + '0');

	BFS(S1, 0), BFS(S2, 1);

	int Result = 1e18;
	for (auto c : D[0])
	{
		if (D[1].count(c.first))
			Result = min(Result, D[0][c.first] + D[1][c.first]);
	}

	if (Result == 1e18) cout << -1 << endl;
	else cout << Result << endl;

	return 0;
}

视频题解

Atcoder Beginner Contest 336 讲解

---

最后祝大家早日