上海计算机学会11月月赛 乙组题解

上海计算机学会11月月赛 乙组题解
本次比赛涉及算法：字符串、贪心、二分、思维、树形动态规划、乘法逆元、状态压缩、折半枚举。

比赛链接：https://iai.sh.cn/contest/57

第一题：T1连接数字

标签：字符串、贪心
题意：给定$n$个十进制正整数$a_1,a_2,\dots ,a_n$，将它们重新排列后拼接起来，尽可能地变成一个大数字，输出这个巨大的数字。$(1<=n<=100000，1<=a_i<=10^{18})$
题解：洛谷 P1012 拼数（原题），很明显需要给这个序列重新排序，然后输出这个序列。那问题就转变成了，需要按什么规则进行排序，这里需要想一个好的贪心策略。

1. 假设按数字大小从大到小排序，很明显能举出一个反例：$111、9$；$1119<9111$
2. 到这步能比较容易想到以字符串的方式读入，似乎更可行点。按字符串字典序从大到小排序，上面是满足了，但是也能举出反例：$32、3$；$323<332$。因为字符串比较，如果能比较的位都一样，认为长的字符串字典序大。
3. 然后我们发现题目中更像是拼接的形式，我们会去考虑把两个字符串$a+b$拼接，或者$b+a$拼接，然后进行比较大小，发现上面的反例都能满足。那我们就认为该贪心策略是对的。贪心策略是否是正确的，很多时候都很难去证明，我们想一道题的贪心策略的时候，多举反例，只要有一个反例，那你当前想的这个策略就是错的，需要想新的贪心策略。（类似 $1、2$）

代码：

#include 
using namespace std;

int n;
string s[100005];

bool cmp(string a, string b) {
    return a + b > b + a;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> s[i];
    sort(s + 1, s + 1 + n, cmp);
    for (int i = 1; i <= n; i++) cout << s[i];
    return 0;
}

第二题：T2桌式足球

标签：二分、贪心、思维
题意：给定一条数轴上$n$个球和$m$个球洞的坐标，球的坐标分别为$x_1,x_2,...,x_n$，球洞的坐标分别为$p_1,p_2,...p_m$。每一轮，可以把所有球整体向左平移一格，或整体右移一格，如果有球经过平移掉入球洞，就会一直待在洞里，后续操作也不会对其有影响，求将所有球落入球洞中，需要的最少操作次数。
（$1\le n,m\le 2\times 10^5,-10^9\le x_i,p_i\le 10^9$，且数据保证没有$x_i=p_j$）
题解：首先，肯定得给这些球和球洞坐标分别从小到大排序。然后观察样例，发现样例是先把所有球往右移动$1$格，再往左移动$4$格最优。

能够想到最终的最少操作次数肯定是：一直往右、一直往左、先往左再往右、先往右再往左 这四种情况中较小次数的那个。

第一步：先去求出每个球分别往左和往右 遇到的第一个球洞的距离，这个部分我们可以通过二分找到第一个大于$x_i$的$p_j$坐标（即第$i$个球右边第一个球洞位置），因为题目中保证没有$x_i=p_j$，找到的$p_{j-1}$是第$i$球左边遇到的第一个球洞位置。如果球的左边或者右边没有球洞，我们设置一下距离无穷大（因为左边或者右边没有球洞，往没有球洞的方向去移动其实没有意义）。

第二步：我们得去考虑 先往左再往右，是不是直接考虑 每个球中往左的距离最大值，再加上每个球中往右的距离最大值即可；发现这个思路其实有问题，因为准备去加的往右的距离最大值的球 可能往左的时候已经掉到球洞里面了。

所以，我们可以二分的时候存每个球离它左/右（$l/r$）第一个球洞的距离放入结构体数组$a$中，我们可以先按$a[i].l$从小到大排序；然后先跑个后缀，求出第$i$个球到第$n$个球中$a[i].r$最大值。

再从前往后枚举一下每个球，因为排序的问题，对于第$i$个球来说，在它之前的球肯定会在往左$a[i].l$的距离下掉入左边的洞；移过去还得移回来，这部分距离得算两次（$2\ast a[i].l$），然后剩下来就得加上第$i+1$到第$n$个球中往右边的最大距离了（这个我们之前维护了一个后缀$suf[i+1]$）。
式子：$ans=min(ans,2\ast a[i].l+suf[i+1])$

第三步：求先往右再往左的，和第二步类似（按$a[i].r$从小到大排序），$suf$要重新维护一下，我这边就直接给出式子了。
式子：$ans=min(ans,2\ast a[i].r+suf[i+1])$
代码：

#include 
using namespace std;

typedef long long ll;
const ll INF = 1e15;
struct node {
    // l/r: 每个球离其 左边/右边 最近球洞的距离
    ll l, r;
}a[200005];

ll n, m, ans = INF;
ll x[200005], p[200005], suf[200005];

bool cmp1(node k1, node k2) {
    return k1.l < k2.l;
}

bool cmp2(node k1, node k2) {
    return k1.r < k2.r;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> x[i];
    for (int i = 1; i <= m; i++) cin >> p[i];

    sort(x + 1, x + 1 + n);
    sort(p + 1, p + 1 + m);

    for (int i = 1; i <= n; i++) {
        ll k = upper_bound(p + 1, p + 1 + m, x[i]) - p;
        a[i].l = x[i] - p[k - 1];
        a[i].r = p[k] - x[i];
        if (k == 1) a[i].l = INF;
        else if (k == m + 1) a[i].r = INF;
    }

    // 先按l从小到大排序 维护一个后缀最大值r
    sort(a + 1, a + 1 + n, cmp1);
    for (int i = n; i >= 1; i--) {
        suf[i] = max(suf[i + 1], a[i].r);
    }
    // 先往左再往右或直接往右 i=0表示直接往右
    for (int i = 0; i <= n; i++) {
        ans = min(ans, 2 * a[i].l + suf[i + 1]);
    }

    sort(a + 1, a + 1 + n, cmp2);
    for (int i = n; i >= 1; i--) {
        suf[i] = max(suf[i + 1], a[i].l);
    }
    // 先往右再往走或直接往左 i=0表示直接往左
    for (int i = 0; i <= n; i++) {
        ans = min(ans, 2 * a[i].r + suf[i + 1]);
    }

    cout << ans;
    return 0;
}

第三题：T3树的匹配

标签：树形$DP$、乘法逆元
题意：给定一棵有$n$个节点的树，根节点为$1$。求这棵树的最大匹配数，并统计最大匹配数情况下的方案数。最终结果，对$10^9+7$取余。树的匹配，指的是具有父子关系的点，两两组成一对，每个点只能在一个配对里。
题解：很明显这是一道树形动态规划。
$dp[u][0/1]$：节点编号为$u$的子树中，$u$不配对/配对时其子树的最大匹配数。
$dp[u][0]={\sum }_{v}Max(dp[v][0],dp[v][1])$
当$u$不配对的时候，把所有孩子节点$v$最大匹配数（$v$不配对或者配对的情况下中的最大值）加起来。
统计完$dp[u][0]$之后，$dp[u][1]$表示的是配对的情况，需要从所有孩子节点$v$没有配对的情况转移过来；当前的孩子节点$v^{\prime }$配对的情况下，其他的孩子节点还是拿$max(dp[v][0],dp[v][1])$。
$dp[u][1]=Ma{x}_j(dp[u][0]-max(dp[v][0],dp[v][1])+dp[v][0]+1)$
这边的$+1$指的是$u$和当前枚举的孩子节点组成的一个新的匹配数。
可以根据下面的图，同学自己再推一推。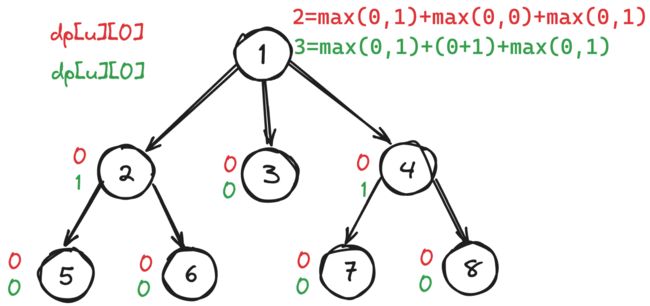

$cnt[u][0/1]$：节点编号为$u$的子树中，$u$不配对/配对时其子树的最大匹配数下的方案数
$cnt[u][0]$其实比较好想，$u$节点既然不配对了，那么只需要管它的所有孩子节点$v$，我们是求最大匹配数的情况下方案数，所以我们得比较一下$dp[v][0]$和$dp[v][1]$中哪个传上来的最大匹配数大，或者一样大。
所以这边我写了一个$select(v)$函数：
$select(v)=dp[v][0]>=dp[v][1]\ast cnt[v][0]+dp[v][0]<=dp[v][1]\ast cnt[v][1]$

ll select(ll v) {
    if (dp[v][0] > dp[v][1]) return cnt[v][0];
    else if (dp[v][0] < dp[v][1]) return cnt[v][1];
    else return (cnt[v][0] + cnt[v][1]) % mod;
}

接下来考虑一下，对于$u$节点来说，所有子树的方案数传上来，是不是得乘积一下（乘法原理）。
公式化：$cnt[u][0]={\prod }_v(select(v))$
然后这边我们从上面的$dp[u][1]$的情况，推一推，上面的是加法原理，然后$u$和某一个孩子节点$v$进行匹配的情况下，我们是先减去$max(dp[v][0],dp[v][1])$，那同理 这边乘法原理，我们要去求$cnt[u][1]$是不是得先除一下。

那接下来我们看实际在什么情况下进行转移，如果在$dp[u][1]$能够变的更大的时候，当然直接从$cnt[v][0]$（$v$不选的情况）的地方转移过来。即$cnt[u][1]=cnt[u][0]/select(v)\ast cnt[v][0]$

那如果当前和之前$dp[u][1]$的值一样，那也就是说有全新的也能够组成最大匹配数的情况，是不是得求和加上来。即$cnt[u][1]=cnt[u][1]+cnt[u][0]/select(v)\ast cnt[v][0]$

需要额外考虑的点是，整道题的方案数最终结果需要取模，除法运算是不符合同余定理的，我们得使用逆元给它转一下。这边通过快速幂去实现一下费马小定理求逆元的。

费马小定理：如果$p$是一个质数，而整数$a$不是$p$的倍数，则有$a^{p-1}\equiv 1(modp)$。
推导得$a^{p-2}=inv(a)(modp)$=> $inv(a)=a^{p-2}(modp)$
代码：

#include 
using namespace std;

typedef long long ll;
const ll mod = 1e9 + 7;

ll n, x;
ll dp[200005][2], cnt[200005][2];
// dp[i][0/1]: i这个顶点不放/放到最终匹配方案中
vector <ll> e[200005];

ll fast_power(ll a, ll b) {
    ll ans = 1;
    a %= mod;
    while (b) {
        if (b & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return ans;
}

ll select(ll v) {
    if (dp[v][0] > dp[v][1]) return cnt[v][0];
    else if (dp[v][0] < dp[v][1]) return cnt[v][1];
    else return (cnt[v][0] + cnt[v][1]) % mod;
}

void dfs(ll u) {
    cnt[u][0] = 1;
    for (int i = 0; i < e[u].size(); i++) {
        ll v = e[u][i];
        dfs(v);
        dp[u][0] += max(dp[v][0], dp[v][1]);
        cnt[u][0] = (cnt[u][0] * select(v)) % mod;
    }
    for (int i = 0; i < e[u].size(); i++) {
        ll v = e[u][i];
        ll otrher = dp[u][0] - max(dp[v][0], dp[v][1]);
        if (dp[u][1] < dp[v][0] + otrher + 1) {
            dp[u][1] = dp[v][0] + otrher + 1;
            ll k = cnt[u][0] * fast_power(select(v), mod - 2) % mod;
            cnt[u][1] = (k * cnt[v][0] + mod) % mod;
        }
        else if (dp[u][1] == dp[v][0] + otrher + 1) {
            ll k = cnt[u][0] * fast_power(select(v), mod - 2) % mod;
            cnt[u][1] = (cnt[u][1] + (k * cnt[v][0]) % mod + mod) % mod;
        }
    }
}

int main() {
    cin >> n;
    for (int i = 2; i <= n; i++) {
        cin >> x;
        e[x].push_back(i);
    }
    dfs(1);
    cout << max(dp[1][0], dp[1][1]) << endl;
    cout << select(1) << endl;
    return 0;
}

第四题：T4平分子集（三）

标签：状态压缩、折半枚举
题意：一个集合被称之为可平分的，如果它可以被分为两部分，且两部分的元素之和相等。空集也算可平分的。给定一个集合$a_1,a_2,a_3,\dots ,a_n$，请统计它有多少子集是可平分的。（本题中所指的集合允许元素相等）（$1<=n<=20，1<=a_i<=10^7$）
题解：看到题目$n$这么小，很容易想到暴力深搜的写法，对于每个数选或不选，然后在选择了的数中再跑一遍深搜看看，能不能分成两部分，然后两部分分别的元素之和相等，试了一下发现这样整体的时间复杂度还是比较大的，并且重复的部分不好处理。

重复的部分，我们会去想 能不能通过状态压缩 把每个数选择的情况根据二进制的情况进行处理一下。针对降低时间复杂度这部分，如果折半枚举题目写的多的同学，应该熟悉这个套路。

每个数有三种情况选择：不选、放在 $A$ 集合、放在 $B$ 集合。
我们设前半部分放到 $A$ 集合内的所有数之和为$a$，放在$B$集合内的所有数之和为$b$。
我们设前半部分放到 $A$ 集合内的所有数之和为$c$，放在$B$集合内的所有数之和为$d$。
那么，$a+c=b+d$，移项得到$a-b=d-c$。（$a-b$其实就是$A$集合所有数之和减去$B$集合所有数之和，$d-c$是$A$集合所有数之和减去$B$集合所有数之和的相反数）

我们先预处理出前半部分的$a-b$情况，去存储一下所有得到当前$a-b$的状态情况（即二进制状态压缩的值），然后后半部分的时候 得到$c-d$情况的时候，去之前存储的部分 找一下有多少$-(c-d)=a-b$的状态。

为了避免重复，我们把着前半部分的对应值的状态和后半部分对应值的状态进行一下按位或，进行结合，标记一下这$n$个数在选择哪些状态的情况下能够达到题目中的要求。
代码：

#include 
using namespace std;

map<int, int> m;
int n, id = 0, a[25], ans[2000005];
vector<int> e[2000005];

// p: 选到第p个数
// sum: A集合所有数之和减去B集合所有数之和
// x: 当前选了哪些数, 二进制 状态压缩
void dfs1(int p, int sum, int x) {
    if (p > n / 2) {
        if (!m[sum]) m[sum] = ++id;
        e[m[sum]].push_back(x);
        return ;
    }
    dfs1(p + 1, sum, x);
    dfs1(p + 1, sum + a[p], x | (1<<(p-1)));
    dfs1(p + 1, sum - a[p], x | (1<<(p-1)));
}

void dfs2(int p, int sum, int x) {
    if (p > n) {
        // 从前半部分的枚举情况下找-sum的形成状态
        int len = e[m[-sum]].size();
        for (int i = 0; i < len; i++) {
            // 维护实际的值的状态 避免重复
            ans[e[m[-sum]][i] | x] = 1;
        }
        return ;
    }
    dfs2(p + 1, sum, x);
    dfs2(p + 1, sum + a[p], x | (1<<(p-1)));
    dfs2(p + 1, sum - a[p], x | (1<<(p-1)));
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    dfs1(1, 0, 0);
    dfs2(n / 2 + 1, 0, 0);
    int res = 0;
    for (int i = 0; i < (1<<n); i++) {
        if (ans[i] == 1) res++;
    }
    cout << res << endl;
    return 0;
}