CCPC 2023 北京市赛 G.【模板】线段树（线段树区间合并20次多项式）

题目

思路来源

lyw

题解

洛谷高仿题目P4247

(ai+x)(ai+x)(ai+x)注意到当x有超过20项时，20个2相乘，对2的20次方取模就为0

所以，维护0次项到19次项乘积的和，向上合并时，是两个多项式卷积，这里暴力相乘即可

下推标记，当下放一个区间加x的标记时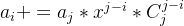，，其中，i

复杂度O(nlogn*20*20)，比较卡常

经典卡常技巧：将取模改成unsigned int自然溢出即可

代码

#include
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef unsigned int ui;
typedef double db;
typedef pair P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<=w)break;
				ui v=x.a[i]*y.a[j];
				add(z.a[i+j],v);
			}
		}
		return z;
	}
	void up(int p){
		e[p]=mer2(e[p<<1],e[p<<1|1]);
	}
	void psd2(node &x,ui v){
		int len=x.r-x.l+1,sz=min(20,len);
		vectorpw(sz+1,1);
		rep(i,1,sz)pw[i]=pw[i-1]*v;
		rep(i,0,sz-1){
			rep(j,i+1,sz){
				ui v=x.a[j]*pw[j-i]*C[j][j-i];
				add(x.a[i],v);
			}
		}
	}
	void psd(int p){
		if(c(p)){
			psd2(e[p<<1],c(p));
			add(c(p<<1),c(p));
			psd2(e[p<<1|1],c(p));
			add(c(p<<1|1),c(p));
			c(p)=0;
		}
	}
	void bld(int p,int l,int r){
		l(p)=l,r(p)=r,c(p)=0;
		if(l==r){
			e[p].a[0]=b[l];
			e[p].a[1]=1;
			return;
		}
		int mid=(l+r)/2;
		bld(p<<1,l,mid);
		bld(p<<1|1,mid+1,r);
		up(p);
	}
	void init(int _n){
		n=_n;
		bld(1,1,n);
	}
	void upd(int p,int ql,int qr,ui x){
		if(ql<=l(p) && r(p)<=qr){
			psd2(e[p],x);
			add(c(p),x);
			return;
		}
		psd(p);
		int mid=(l(p)+r(p))/2;
		if(ql<=mid)upd(p<<1,ql,qr,x);
		if(qr>mid)upd(p<<1|1,ql,qr,x);
		up(p);
	}
	node ask(int p,int ql,int qr){
		if(ql<=l(p) && r(p)<=qr){
			return e[p];
		}
		psd(p);
		int mid=(l(p)+r(p))/2;
		if(ql<=mid && qr>mid){
			node L=ask(p<<1,ql,qr);
			node R=ask(p<<1|1,ql,qr);
			node res=mer2(L,R);
			return res;	
		}
		else if(ql<=mid){
			node L=ask(p<<1,ql,qr);
			return L;
		}
		else{
			node R=ask(p<<1|1,ql,qr);
			return R;
		}
	}
}seg;
void init(){
	C[0][0]=1;
	int up=21;
	rep(i,1,up){
		C[i][0]=C[i][i]=1;
		rep(j,1,i-1){
			C[i][j]=(C[i-1][j]+C[i-1][j-1]);
		}
	}
}
int op,l,r;
ui x;
int main(){
	init();
	sci(n),sci(q);
	rep(i,1,n)scanf("%u",&b[i]);
	seg.init(n);
	rep(i,1,q){
		scanf("%d%d%d",&op,&l,&r);
		if(op==1){
			scanf("%u",&x);
			seg.upd(1,l,r,x);
		}
		else{
			printf("%u\n",seg.ask(1,l,r).a[0]&mod);
		}
	}
	return 0;
}