【数据结构】线性表

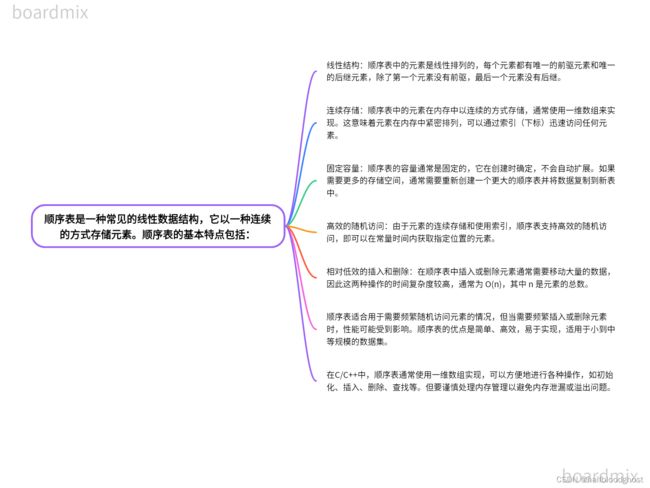
顺序表是一种常见的线性数据结构，它以一种连续的方式存储元素。顺序表的基本特点包括：

1. 线性结构：顺序表中的元素是线性排列的，每个元素都有唯一的前驱元素和唯一的后继元素，除了第一个元素没有前驱，最后一个元素没有后继。

2. 连续存储：顺序表中的元素在内存中以连续的方式存储，通常使用一维数组来实现。这意味着元素在内存中紧密排列，可以通过索引（下标）迅速访问任何元素。

3. 固定容量：顺序表的容量通常是固定的，它在创建时确定，不会自动扩展。如果需要更多的存储空间，通常需要重新创建一个更大的顺序表并将数据复制到新表中。

4. 高效的随机访问：由于元素的连续存储和使用索引，顺序表支持高效的随机访问，即可以在常量时间内获取指定位置的元素。

5. 相对低效的插入和删除：在顺序表中插入或删除元素通常需要移动大量的数据，因此这两种操作的时间复杂度较高，通常为 O(n)，其中 n 是元素的总数。

顺序表适合用于需要频繁随机访问元素的情况，但当需要频繁插入或删除元素时，性能可能受到影响。顺序表的优点是简单、高效，易于实现，适用于小到中等规模的数据集。

在C/C++中，顺序表通常使用一维数组实现，可以方便地进行各种操作，如初始化、插入、删除、查找等。但要谨慎处理内存管理以避免内存泄漏或溢出问题。

请对顺序表中的线性表进行分析，叙述其逻辑结构和存储结构两个层次的含义及相互关系

线性表是一种常见的数据结构，通常包括逻辑结构和存储结构两个层次的概念。

1. 逻辑结构：

   • 逻辑结构是关于数据之间关系和组织的高层次抽象。在线性表中，逻辑结构定义了元素之间的线性排列关系，也就是它们是按照一定的顺序排列的。

   • 线性表的逻辑结构意味着数据元素之间存在明确的前后关系，即每个元素都有唯一的前驱元素和唯一的后继元素，除了首元素没有前驱，尾元素没有后继。这种排列关系通常用线性结构的方式来表示。

2. 存储结构：

   • 存储结构是关于如何在计算机内存中组织和存储数据的实际方式。它关注数据在计算机内存中的物理存储表示。

   • 在顺序表中，存储结构通常通过一维数组来实现。数组中的每个元素对应于线性表中的一个数据元素，它们在内存中是依次紧密排列的。这种存储结构被称为顺序存储结构，因为数据元素按顺序存储在内存中。

   • 顺序表的存储结构使得元素的访问非常高效，因为你可以通过下标迅速访问任何元素。然而，它的缺点是插入和删除元素时可能需要移动大量的数据。

相互关系：

• 逻辑结构和存储结构之间的关系是，逻辑结构定义了数据元素之间的逻辑关系，而存储结构定义了如何在计算机内存中实际存储这些数据元素。

• 在顺序表中，逻辑结构要求元素之间的线性排列，存储结构通过使用一维数组来满足这一要求。数组的索引对应于逻辑顺序中的位置。

• 存储结构是为了满足逻辑结构而设计的，它提供了一种有效的方式来组织数据以便快速访问和操作。在顺序表中，逻辑结构和存储结构之间有一个紧密的对应关系。

总之，逻辑结构定义了数据元素之间的逻辑关系，而存储结构定义了如何在计算机内存中实际存储这些数据元素，两者之间相互关联以实现线性表的定义和操作。

以下提供一个具体的示例，演示逻辑结构和存储结构之间的关系，以及如何在C++中实现线性表的顺序存储结构。

#include 
using namespace std;

// 定义线性表的最大容量
const int MAX_SIZE = 100;

// 顺序表的逻辑结构：线性排列的整数元素
struct LinearList {
    int data[MAX_SIZE]; // 数据域，存储整数元素
    int length;         // 当前线性表的长度
};

// 初始化线性表，将长度设置为0
void initLinearList(LinearList &list) {
    list.length = 0;
}

// 向线性表中插入元素
bool insertElement(LinearList &list, int element, int position) {
    if (position < 0 || position > list.length || list.length >= MAX_SIZE) {
        return false; // 插入位置无效或线性表已满
    }

    // 将插入位置之后的元素向后移动一位
    for (int i = list.length; i > position; i--) {
        list.data[i] = list.data[i - 1];
    }

    // 插入新元素
    list.data[position] = element;
    list.length++;
    return true;
}

// 输出线性表的元素
void displayLinearList(const LinearList &list) {
    for (int i = 0; i < list.length; i++) {
        cout << list.data[i] << " ";
    }
    cout << endl;
}

int main() {
    LinearList myList;
    initLinearList(myList);

    // 向线性表中插入元素
    insertElement(myList, 1, 0);
    insertElement(myList, 2, 1);
    insertElement(myList, 3, 2);

    // 输出线性表的元素
    cout << "Elements in the linear list: ";
    displayLinearList(myList);

    return 0;
}

在这个示例中，我们定义了一个包含逻辑结构的线性表 LinearList，它包括一个整数数组 data 来存储元素，以及一个 length 变量来跟踪当前线性表的长度。我们使用了逻辑结构的概念，确保元素按线性顺序排列。

在存储结构方面，我们使用了一维数组 data，它用于实际存储线性表的元素。在 insertElement 函数中，我们实现了在线性表中插入元素的操作，其中包括了数组元素的移动。最后，我们使用 displayLinearList 函数输出线性表的元素。

这个示例演示了逻辑结构（线性排列的整数元素）与存储结构（使用整数数组）之间的关系，并展示了如何在C++中实现线性表的顺序存储结构。

顺序表中基本操作的实现包括初始化、取值、按位查找、按值查找、插入、删除。请代码实现并进行算法分析，并指出他们各自的时间复杂度和空间复杂度。

在顺序表中，常见的基本操作包括初始化、取值、按位查找、按值查找、插入和删除。下面我将为每个操作提供代码实现以及相应的时间复杂度和空间复杂度分析。

1. 初始化操作：

   • 初始化顺序表，将长度设置为0。

   // 初始化操作
   void initLinearList(LinearList &list) {
       list.length = 0;
   }
   

   • 时间复杂度：O(1)
   • 空间复杂度：O(1)

2. 取值操作：

   • 根据给定位置（下标）获取顺序表中的元素。

   // 取值操作
   int getElement(const LinearList &list, int position) {
       if (position >= 0 && position < list.length) {
           return list.data[position];
       } else {
           return -1; // 返回一个特定值表示越界或错误
       }
   }
   

   • 时间复杂度：O(1)
   • 空间复杂度：O(1)

3. 按位查找操作：

   • 根据元素值查找其在顺序表中的位置（下标）。

   // 按位查找操作
   int findElementByPosition(const LinearList &list, int element) {
       for (int i = 0; i < list.length; i++) {
           if (list.data[i] == element) {
               return i; // 找到元素，返回位置
           }
       }
       return -1; // 未找到元素，返回-1表示失败
   }
   

   • 时间复杂度：O(n)（最坏情况下需要遍历整个顺序表）
   • 空间复杂度：O(1)

4. 按值查找操作：

   • 根据给定位置查找顺序表中的元素值。

   // 按值查找操作
   int findPositionByElement(const LinearList &list, int position) {
       if (position >= 0 && position < list.length) {
           return list.data[position];
       } else {
           return -1; // 返回一个特定值表示越界或错误
       }
   }
   

   • 时间复杂度：O(1)
   • 空间复杂度：O(1)

5. 插入操作：

   • 在指定位置插入元素，需要将插入位置之后的元素向后移动。

   // 插入操作
   bool insertElement(LinearList &list, int element, int position) {
       if (position >= 0 && position <= list.length && list.length < MAX_SIZE) {
           // 将插入位置之后的元素向后移动
           for (int i = list.length; i > position; i--) {
               list.data[i] = list.data[i - 1];
           }
           list.data[position] = element;
           list.length++;
           return true;
       } else {
           return false; // 插入位置无效或顺序表已满
       }
   }
   

   • 时间复杂度：O(n)（最坏情况下需要移动 n 个元素）
   • 空间复杂度：O(1)

6. 删除操作：

   • 删除指定位置的元素，需要将删除位置之后的元素向前移动。

   // 删除操作
   bool deleteElement(LinearList &list, int position) {
       if (position >= 0 && position < list.length) {
           // 将删除位置之后的元素向前移动
           for (int i = position; i < list.length - 1; i++) {
               list.data[i] = list.data[i + 1];
           }
           list.length--;
           return true;
       } else {
           return false; // 删除位置无效
       }
   }
   

   • 时间复杂度：O(n)（最坏情况下需要移动 n 个元素）
   • 空间复杂度：O(1)

以上是顺序表的基本操作及其时间复杂度和空间复杂度的分析。请注意，时间复杂度和空间复杂度是根据算法执行的最坏情况来估算的，实际性能可能会更好。

优化初始化
在实际编程中，初始化顺序表时应该分配一个大小为 MAX_SIZE 的数组，同时需要确保内存分配是否成功。这可以提高代码的健壮性，并防止潜在的内存溢出问题。以下是经过修改的初始化操作：

// 初始化操作
bool initLinearList(LinearList &list) {
    list.length = 0;
    list.data = new int[MAX_SIZE];
    if (!list.data) {
        // 内存分配失败，显示溢出并返回错误
        cerr << "Memory allocation failed (overflow)." << endl;
        return false;
    }
    return true;
}

这个初始化操作将首先尝试分配一个大小为 MAX_SIZE 的整数数组，然后检查内存分配是否成功。如果分配失败，它会显示溢出错误并返回 false，否则返回 true 表示初始化成功。

这种健壮的做法确保了在内存不足或分配失败的情况下能够适当地处理问题，避免了潜在的崩溃或内存问题。

---

- 注cerr：

---

cerr 是 C++ 中的标准错误输出流，通常用于向标准错误设备（通常是终端或控制台）输出错误消息。它是 C++ 标准库的一部分，对应于 C 语言中的 stderr。

与 cout（标准输出流）类似，cerr 也用于输出信息，但它的主要目的是输出错误信息，以便开发人员能够更容易地识别和调试程序中的问题。与 cout 不同，cerr 通常不会被缓冲，这意味着消息会立即显示在终端上，而不会等待缓冲区填满或遇到换行符等情况。

在 C++ 中，你可以使用 cerr 来输出错误消息，例如：

#include 
using namespace std;

int main() {
    int denominator = 0;
    if (denominator == 0) {
        cerr << "Error: Division by zero." << endl;
    }
    return 0;
}

在上面的示例中，如果 denominator 的值为零，程序将输出错误消息到标准错误流 cerr，以指示发生了除零错误。这有助于开发人员识别问题并进行调试。