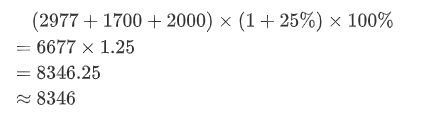JMU第十五届蓝桥校选--菜鸡的92分伪题解
校选打完了 还是没进前十┭┮﹏┭┮
大佬的题解真看不懂 所以自己写了一篇
填空第一题和编程前五题满分题解,后面暴力+骗分(啊反正不是正解)
填空题
题目:
今天是2023年11月22日,小明想知道在 [2023,20231122] 范围内有多少个整数出现过 1122 。
例如: 整数 11122122 出现过 1122 ,整数 11322 没有出现过 1122 。
题解:
字符串判断,判断1122是否在字符串里面 可以用python 把数字转成字符再判断
代码:
ss="1122"
ans=0
for i in range(2023,20231123):
s=str(i) #数字转化成字符串
if(ss in s):#如果1122在这个字符串里 就加一
ans+=1
print(ans)编程题
题目1:
7-1 JMU最菜的人是谁?分数:5
问题描述】
显然善良的贝贝不会为难来签到的你的~
请回答出“集美大学最菜的人是谁?”这个问题的答案
这道题答案是众所周知的。
你只需要输出“林贝宁是集美大学最菜的人”这句话的全拼,出题人就会因为你的诚实可贵而奖励你5分。
【输入格式】
本题无输入。
【输出格式】
仅一行,包含一个字符串,为“林贝宁是集美大学最菜的人”这句话的全拼,每个汉字的拼音之间请使用空格隔开。
【样例输入】
这题当然没有输入
【样例输出】
这里当然也没有输出~
【提示】
提示1:假如你需要输出“王丹薇是集美大学最强的人”的全拼
- 则你的输出应该为:
wang dan wei shi ji mei da xue zui qiang de ren - 但本题并不要求你输出这句话,而是输出“林贝宁是集美大学最菜的人”这句话的全拼,此处仅做举例。
提示2:
- 考虑到你可能是一个土生土长的南方人,你可能区分不了
l和n,以及in和ing。 - 但你是一位熟练使用手机输入法的大学生,善良的出题人提醒你,使用本机的中文输入法是合法的,你可以以此来得到
林和宁的全拼。
提示3:
- 复制提示1的全拼字符串时,记得将“最强的”替换为“最菜的”哦
题解:
直接输出 用python写的少一点点 “林”的拼音没有g
代码:
print("lin bei ning shi ji mei da xue zui cai de ren")题目2:
7-2 烽火大都督 分数10
问题描述】
贝贝平时最大的乐趣,就是在闲暇的时候,开一把紧张刺激的《王(dan)者(zai)荣(pai)耀(dui)》。
而贝贝最喜欢的英雄莫过于“烽火大都督”——周瑜
- 两年半前,他曾日夜不停的刷着荣耀战力
- 终于以9055的荣耀战力,成为了全村第一周瑜,最终成功当上了村里的烧烤摊老板(bushi
而荣耀战力的计算公式如下:荣耀战力 =(胜场战力+排位表现分+巅峰战力)*(1 + 巅峰系数)*(活跃系数)
请你写一个程序,帮贝贝计算他的荣耀战力。
【输入格式】
仅一行,包含5个整数a,b,c,d,e,分别表示贝贝的某个英雄的胜场战力、排位表现分、巅峰战力、巅峰系数、活跃系数。
其中巅峰系数和活跃系数,将以百分数的形式给出(不含百分号)。
【输出格式】
仅一行,包含一个整数,表示贝贝的某个英雄的荣耀战力。
【样例输入】
2977 1700 2000 25 100
【样例输出】
8346
【样例解释】
【评测用例规模与约定】
对于100%的数据,0≤a≤3000,0≤b≤3000,0≤c≤10000,0≤d,e≤100。
注1:关于输出
- 由于公式的计算结果可能不是整数,所以你需要保留0位小数输出,即将最终的结果四舍五入。
注2:关于判题程序
- 考虑到你的程序中可能会有精度问题,若你的答案跟正确答案相差1,善良的贝贝也认为你是正确的。
- 简言之,我们放宽了要求,若你的答案为X,标准答案为Y,当∣X−Y∣≤1时,你的答案被认为是正确的。
注3:关于“格式错误”
- 因为本题采用特殊评测机制。若你的答案输出的是小数,会优先返回“格式错误”(并不会检测你的答案是否正确)。
- 所以请严格按照题意输出一个整数。另外多余的行末空格,在本题中也会导致“格式错误”。
题解:
模拟题,主要是最后要保留0位小数 所以用c++里的fixed setprecision(0)来保留就行
代码:
#include
using namespace std;
int main()
{
double a,b,c,d,e;
cin>>a>>b>>c>>d>>e;
d=d/100;
e=e/100;
double ans=(a+b+c)*(1+d)*e;
cout< 题目3:
7-3 背单词 分数:15
问题描述】
小明正在为四级做准备,他计划至少背 n 个新单词。
为了完成这个目标,小明决定在每天结束前背一些新单词,具体来说:
- 第 1 天结束前,小明会背 m 个新单词;
- 第 i 天(i≥2)结束前,小明会根据第 i−1 天背的单词数计算第 i 天背多少个新单词
假设小明在第 i−1 天背了 t 个新单词:- 如果 t 是奇数,小明将会在第 i 天结束前背 3×t+1 个新单词;
- 如果 t 是偶数,小明将会在第 i 天结束前背 2t 个新单词。
现在小明想知道按照这个方式背单词,最早在第几天结束时累计背了至少 n 个新单词。
【输入格式】
输入一行,包含两个整数 n,m ,分别代表小明计划背的新单词总数和小明第一天背的新单词数量。
【输出格式】
输出一行,包含一个整数 d ,代表小明在第 d 天结束时累计背了至少 n 个新单词。
【样例输入】
100 100
【样例输出】
1
第一天背了 100 个新单词,最早在第一天结束时完成背至少 100 个新单词的计划。
【样例输入】
100 50
【样例输出】
3
第一天背了 50 个新单词,第二天背了 25 个新单词,第三天背了 76 个新单词,累计背了 151 个新单词,最早在第三天结束时完成了背至少 100 个新单词的计划。
【评测用例规模与约定】
对于 60% 分数的评测用例,1≤n≤106,1≤m≤1000 。
对于 100% 分数的评测用例,1≤n≤1012,1≤m≤1000 。
题解:
用暴力模拟可以得9分 但是n最大是10^12 会超时
枚举一下会发现 最后都会进入4 2 1 4 2 1的循环 所以遇到这种情况 可以把4 2 1这三天为一组,总的为7,可以快速减少循环次数
代码:
#include
using namespace std;
#define ll long long
ll n,m;
ll day;
int main()
{
cin>>n>>m;
while(n>0)
{
n-=m;
day++;
//现正常模拟
if(m%2==0)
{
m/=2;
}
else
{
m=3*m+1;
}
//遇到最终的情况了
if(m==1||m==2||m==4)
{
day+=(n/7)*3;//4+2+1=7 三天为一组
n%=7;
}
}
cout< 题目4:
7-4 堆 分数:15
【问题描述】
在本题中,你需要实现一个数据结构,它需要支持以下操作:
- 插入:给定整数x,将数x插入该数据结构中。
- 删除:将该数据结构的其中一个最小值从该数据结构中删除。
- 加法:给定整数x,将该数据结构中的所有元素全部加上x。
对于每个操作2,你需要输出被删除的值。
【输入格式】
第一行包含一个正整数 Q(2≤Q≤106),Q表示操作的次数。
接下来Q行,每行将以下方的格式来描述每次操作:
1 x:表示题目描述中的操作1。2:表示题目描述中的操作2。3 x:表示题目描述中的操作3。
对于操作1和操作3的x满足∣x∣≤109。
保证每次操作2时该数据结构内至少有一个元素。
具体可见样例。
【输出格式】
输出包含若干行,每行有一个整数。第i行的整数表示第i次操作2所删除的数的大小。
【样例输入】
13
1 1
1 1
1 2
1 3
1 4
2
3 10
2
1 1
2
1 12
2
2
【样例输出】
1
11
1
12
12
【评测用例规模与约定】
对于40%分数的数据,满足∣x∣≤109,2≤Q≤1000。
对于100%的数据,满足∣x∣≤109,2≤Q≤106。
题解:
用priority_queue优先队列可以自动把放入的元素从小到大排序 然后依次取出
难点在于怎么把全部加上x后不超时
定义一个add 用来存加了多少数 每次1操作要加入x的时候 在堆里加(x-add)可以保证大小顺序不变 然后在3操作加x的时候 add+=x 在2操作删除的时候 输出当前最小的值+add 这样就能保证新加入的数不会受之前的影响
代码:
#include
using namespace std;
#define ll long long
priority_queue ,greater > q;//优先队列 greater是自动从小到大排序
ll add;
int main()
{
ios::sync_with_stdio(0);//关流加速
cin.tie(0);
cout.tie(0);
int Q;
cin>>Q;
while(Q--)
{
int op;
cin>>op;
if(op==1)
{
ll x;
cin>>x;
q.push(x-add);//用add来控制
}
else if(op==2)
{
cout<>x;
add+=x;
}
}
return 0;
} 题目5:
7-5 玩《Minecraft》的贝贝 分数:15
问题描述】
贝贝通过./give指令获得了n个木棍和m个钻石,以及一个工作台,他想要制造尽可能多的工具。
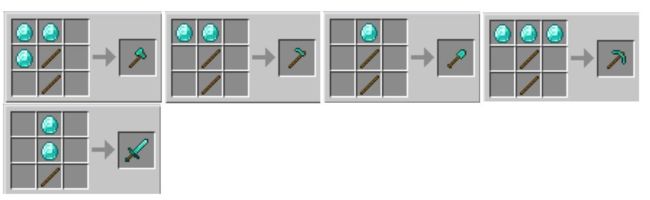
一共有五种钻石工具,下面是每种钻石工具的合成方案:
【输入格式】
第一行,一个整数,为数组组数T。
接下来的T行,每行两个以空格分隔的整数n,m。
【输出格式】
输出T行,每行一个整数,表示该组数据可制作工具数量的最大值。
【样例输入】
3
2 9
5 4
6 7
【样例输出】
2
3
4
【评测用例规模与约定】
对于20%的数据,1≤T≤5,0≤n,m≤20。
对于100%的数据,1≤T≤105,0≤n,m≤109。
伪题解:
因为要制造最多的工具数量,所以制造工具所用的材料当然越少越好 所以只有2钻石1木棍和1钻石2木棍的组合可以选择
设2 1的个数有x个
设1 2的个数有y个
求x+y的max
木棍不能超过n个 所以2x+y<=n
钻石不能超过m个 所以x+2y<=m
所以x+y<=(n+m)/3
再判断现在的这个max是否比木根和钻石的最小值谁大
因为如果在达到这个最大值之前 木棍或者钻石用完了 就已经结束了
代码:
#include
using namespace std;
#define ll long long
int main()
{
int t;
cin>>t;
while(t--)
{
ll n,m;
cin>>n>>m;
ll temp=(n+m)/3;
ll ans=0;
if(temp>=min(n,m))
{
ans=min(n,m);
}
else{
ans=temp;
}
cout< 题目6:
7-6 卯酉东海道 分数:20
问题描述】
琪露诺想找三月精一起玩。她计划乘坐广重 36 号列车从雾之湖去到博丽神社。
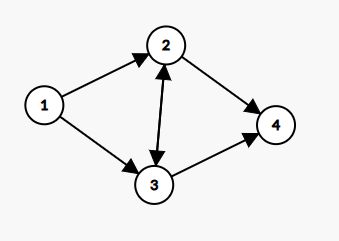
整个隙间交通网络目前具有 n 个站台,但是由于需要收费,因而每个通道都是单向道路,同时每条通道具有一定的颜色和费用(冰块)。总的隙间通道一共有 m 条,总的通道颜色一共有 l 种。
琪露诺有一张通行卡,在她出发前,她可以任意染色该通行卡而不花费费用。当通行卡的颜色与琪露诺想要经过的通道颜色相同时,琪露诺就可以借助该通路到达下一站,花费这条道路的冰块数 w。若通行卡的颜色与琪露诺想要经过的通道颜色不相同,琪露诺需要支付冰块数 base×w ,同时将通行卡颜色改为该通道的颜色后,才可通过。
现在琪露诺在 1 号雾之湖站,要去 n 号博丽神社站。问在最优决策的情况下,琪露诺需要最少花费多少冰块。
【输入格式】
输入的第一行包括三个正整数 n,m,l,base ,分别表示节点的个数、边的个数、所有通道的颜色种类数量,通行卡改变颜色时的费用倍率。
接下来 m 行,表示该隙间交通网络的总边数。每一行给出三个正整数 u,v,col,w ,表示一条从 u 到 v 、颜色为 col 、支付冰块数为 w 的有向边。
【输出格式】
如果不存在任何方案,则输出一行一个整数 −1 。否则输出整数,表示在最优决策下,琪露诺从 1 到达 n 最少花费的冰块数。
【样例输入】
4 6 3 2
1 2 1 3
1 3 3 2
2 4 2 2
3 4 1 3
2 3 1 10
3 2 3 5
【样例输出】
7
【样例输入】
10 1 1 1
1 2 1 14
【样例输出】
-1
【样例解释】
对于第一个样例,最佳路径为 1→2→4 ,颜色变化为 1→2 ,费用为 3+2×2=7 。
对于第二个样例,由于没有从 1 到达 v 的路径,因而无解。
【评测用例规模与约定】
对于 20% 分数的数据有:l=1 。
对于 20% 分数的数据有:n≤100 。
对于 100% 的测试点,保证 1≤n≤5×103,1≤m≤3×105,1≤l≤64,2≤base≤4 。
对于 100% 的测试点,保证 1≤u,v≤n ,1≤col≤l,1≤w≤108 ,保证没有自环。
伪题解:
一看就是dp的题 但我不会
输出-1可以骗1分 over
题目7:
7-7 简单的背包问题 分数:20
问题描述】
这是一个背包问题。
你有n个物品,其中第i个物品的重量为wi,价值为vi。
现给定Q次询问,每次询问给出一个背包上限W,在总重量不超过背包上限W的情况下,最大化装入背包的物品的价值。
【输入格式】
第一行包含一个正整数 n,n表示物品数量。
接下来n行,每行给出两个正整数wi,vi,其中第i个wi表示第i个物品的重量,第i个wi表示第i个物品的价值。
接下来有一个数Q,表示询问次数。
每次询问只有一行,包含一个正整数W,W的意义见题目描述。
【输出格式】
输出Q行,第i行表示第i次询问的答案。
【样例输入】
2
2 3
3 4
4
2
3
4
5
【样例输出】
3
4
4
7
【评测用例规模与约定】
对于30%的数据,1≤n≤10,1≤wi≤100,1≤vi≤100,1≤Q≤1000,1≤W≤1000。
对于60%的数据,1≤n≤100,1≤wi≤100,1≤vi≤100,1≤Q≤1000,1≤W≤10000。
对于100%的数据,1≤n≤100,1≤wi≤109,1≤vi≤100,1≤Q≤105,1≤W≤1011。
伪题解:
乍一看好像就是一个动态规划---背包的题目 但是数据范围太大了 正解用了二分
我只会裸背包 所以暴力12分
用背包的模板就可以有12分
代码:
#include
using namespace std;
#define ll long long
ll n;
ll w[100005],v[100005];
ll dp[100005];
ll Q;
ll W;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
}
cin>>Q;
while(Q--)
{
cin>>W;
//每一次都要重置dp数组 否则会出问题
for(int i=1;i<=W;i++)
{
dp[i]=0;
}
//背包模板
for(int i=1;i<=n;i++)//背包个数
{
for(int j=W;j>=w[i];j--)//从背包容量开始往下循环
{
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout< 题目8:
7-8 響符「パワーレゾナンス」 分数:25
【问题描述】
幽谷响子最近在妖怪之山中依靠回声朗诵经文。
她事先已经朗诵过 n 篇经文,其中第 i 篇经文回声的响度为 ai 。由于城管正在妖怪之山泡温泉,因而她计划在执行完 q 次操作后立刻离开。
响子酱的操作有以下两种:
1 l r:表示响子酱根据所有满足 l≤i≤r 的经文回声响度 ai ,再次进行朗诵,即 ai=F(ai);2 l r:表示响子酱接收所有满足 l≤i≤r 的的经文响度 ai 后,在本子上记录下一行,一行只有一个数字,表示 ∑i=lrai ,即经文响度之和。
其中,响子再次朗诵经文的操作 F(x) 表示如下。
F(x)=2⌊3x2+1∣x3−3x∣⌋
在响子执行完 q 次操作以后,她在本子上记录的内容是什么呢?
⌊x⌋ 为向下取整,即 ⌊1.9⌋=1,⌊2⌋=2 。
【输入格式】
第一行,两个正整数 n,q ,分别表示响子酱朗诵的经文数与其操作数。
第二行,给出 n 个整数,表示响子酱事先朗诵经文的响度 ai ,i 从 1 开始。
接下来 q 行,每行给出三个正整数 opt,l,r 。
- 若 opt=1 ,表示第一种操作,即对于区间 [l,r] 内的每个响度 x ,x=F(x) ;
- 若 opt=2 ,表示第二种操作,即输出对于区间 [l,r],响度之和 ∑i=lrai 。
【输出格式】
对于每一个 opt=2 的操作,输出单独一行一个数字,表示询问区间 [l,r] 经文的响度之和 ∑i=lrai。
【样例输入】
1 3
114
2 1 1
1 1 1
2 1 1
【样例输出】
114
74
【样例输入】
5 5
114 514 1919 810 495
2 1 5
1 1 4
2 4 5
1 3 5
2 2 4
【样例输出】
3852
1033
1550
【样例解释】
对于第一个样例,其计算过程如下:
F(114)=2×⌊3×1142+1∣1143−3×114∣⌋=2×⌊389891481202⌋=2×37=74
【评测用例规模与约定】
对于 20% 分数的数据,保证 1≤n,q≤102 。
对于 40% 分数的数据,保证 1≤n≤5×104,1≤q≤105 。
对于 100% 的数据,保证 1≤n≤105,1≤q≤3×105。
对于所有的 ai ,保证 0≤ai≤106 。
对于所有的 opt ,保证 opt∈{1,2} 。
对于所有的 l,r ,保证 1≤l≤r≤n 。
伪题解:
这个要用线段树 但是好长哦 不太会
根据题意模拟能5分
用快读加速一下能8分 快读yyds
代码:
#include
using namespace std;
#define ll long long
ll n,q;
ll a[100005];
inline ll read()//快速读入的模板
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
ll F(ll x)//模拟题目的函数
{
return 2*(abs(x*x*x-3*x)/(3*x*x+1));
}
int main()
{
//cin>>n>>q;
n=read();
q=read();
for(int i=1;i<=n;i++)
{
//cin>>a[i];
a[i]=read();
}
while(q--)
{
int op;
//cin>>op;
op=read();
ll l,r;
//cin>>l>>r;
l=read();
r=read();
if(op==1)
{
//暴力循环他丫的
for(int i=l;i<=r;i++)
{
a[i]=F(a[i]);
}
}
else if(op==2)
{
ll sum=0;
for(int i=l;i<=r;i++)
{
sum+=a[i];
}
cout< 题目9:
7-9 平方数 分数:25
【问题描述】
贝贝有一个长度为 n 的序列 A,第 i 个元素为 Ai,贝贝现在需要选出一些下标,并且需要使得选出的这些下标中没有任意一对 (i,j) 下标对应的 Ai×Aj 是一个平方数,你需要输出贝贝最多能选出多少个下标。
【输入格式】
第一行,一个数字 n 表示数组长度
第二行, n 个正整数表示给定的 A 序列。
【输出格式】
一行一个整数表示最多能选出的下标个数。
【样例输入】
5
1 1 2 3 4
【样例输出】
3
【样例输入】
7
1 3 2 5 4 9 1
【样例输出】
4
【评测用例规模与约定】
对于 32% 分数的数据有 : n≤1000,Ai≤106
对于 60% 分数的数据有 : n≤105,Ai≤106
对于 100% 分数的数据有 :1≤n≤105,1≤Ai≤109
伪题解:
考试的时候没啥思路 但是能骗分 从0开始往上一个个输出 或者从n往下一个个减小输出
输出n-2就能骗3分
题目10:
7-10 贝贝的石子游戏 分数:30
【问题描述】
贝贝在玩一个石子游戏。n个石子按从左往右的顺序排成一行,每个石子有一个重量和一个类型,类型分为A和B两种。其中第i个石子的类型为si,其重量为wi。
- 贝贝可以进行n次操作,每次选择一个石子将其移走。
- 显然,最终所有石子都将被移走。
在这个过程中,你的得分如下:
- 对于一次操作,假设贝贝要移走第j个石子(初始编号):
- 如果石子j是还未移走的石子中最左侧或最右侧的石子,则得分为0。
- 若与石子j相邻的两个石子中(当前状态,不是初始状态),存在一个石子的类型与其相同,则得分为0。
- 否则,得分为wj。
- 整个过程的得分为所有操作的得分之和。
贝贝的目标是最大化最终的得分。但是众所周知贝贝是个菜狗,于是他向聪明的你寻求帮助,请你写一个程序告诉他得分的最大值为多少。
【输入格式】
第一行,包含一个整数 n。
第二行,包含一个长为 n 的字符串 S=s1s2⋯sn,每个字符只可能为 A 或 B,描述该石子的类型。
第三行,包含 n 个整数 w1,w2,⋯,wn,描述每个石子的重量。
【输出格式】
仅一行,包含一个整数,表示最大的得分。
【样例输入1】
3
ABA
1 2 3
【样例输出1】
2
【样例输入2】
7
AABBABA
2 4 5 1 3 7 6
【样例输出2】
12
【评测用例规模与约定】
对于至少 10% 分数的数据有:1≤n≤3
对于至少 20% 分数的数据有:1≤n≤8
对于至少 30% 分数的数据有:1≤n≤20
对于至少 50% 分数的数据有:1≤n≤1000
对于至少 70% 分数的数据有:1≤n≤105
对于 100% 的数据有:1≤n≤106,1≤wi≤109。
伪题解:
传说中给验题人做的压轴题
但是一看范围 诶嘿 最小是n<=3
那可以先枚举一下n=1 2 3 的情况 看看会发生什么 然后就骗了3分
代码:
#include
using namespace std;
int a[100];
int main()
{
int n;
cin>>n;
string s;
cin>>s;
int maxn=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
if(n==1)//只有一种可能
{
cout<<0< 全屏浏览题目
切换布局