day14 二叉树part1
统一迭代法只搞懂了大概,真的没时间再写了。二刷的你如果有时间可以再琢磨琢磨,思路我理了个大概了。
(labuladong)先在开头总结一下,二叉树解题的思维模式分两类:
1、是否可以通过遍历一遍二叉树得到答案?如果可以,用一个 traverse 函数配合外部变量来实现,这叫「遍历」的思维模式。
2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn,注意我这里没有说unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。(这个我还真不清楚,等以后再补吧,先记下了)
所以大家使用自己熟悉的编程语言写算法,一定要知道常用的容器底层都是如何实现的,最基本的就是map、set等等,否则自己写的代码,自己对其性能分析都分析不清楚!
前置知识
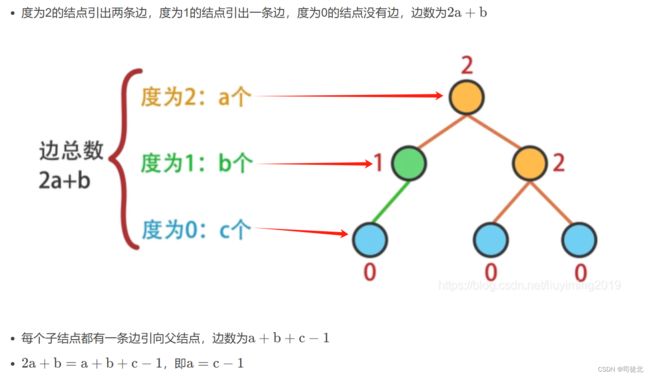
①度:(我的理解:就是这个节点有几条边的意思)
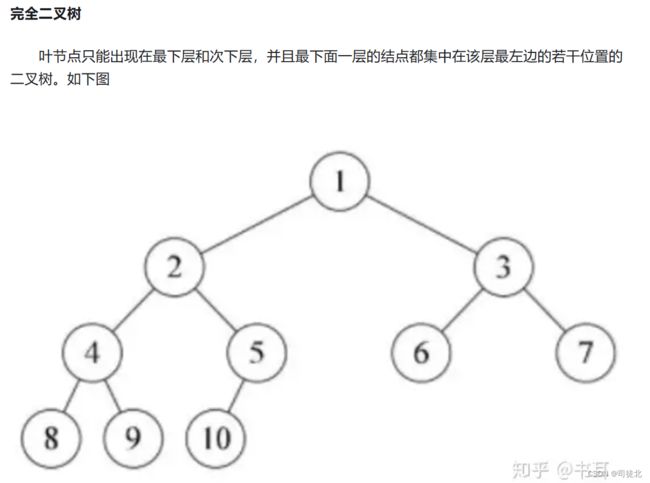
②在我们解题过程中二叉树有两种主要的形式:满二叉树和完全二叉树。
图片引自:满二叉树和完全二叉树 - 书耳的文章 - 知乎
https://zhuanlan.zhihu.com/p/152285992

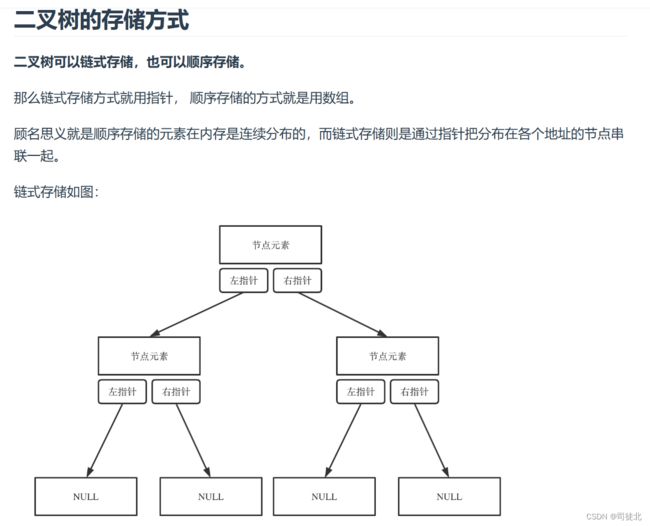

二叉树主要有两种遍历方式:
①深度优先遍历:先往深走,遇到叶子节点再往回走。
②广度优先遍历:一层一层的去遍历。
以下内容来自:
一文搞懂二叉树的前序遍历,中序遍历,后序遍历 - 育树霖疯的文章 - 知乎
https://zhuanlan.zhihu.com/p/404837352
所谓前序,中序,后续遍历命名的由来是我们访问二叉树,根节点的顺序。前序遍历就是优先访问根节点,中序遍历是第二个访问根节点,后续遍历就是访问完左右节点之后,最后访问根节点。注意访问二字。访问和获取是两个不同的概念,我们可以获取一个节点,但是不访问他。对应在计算机里的概念是,获取一个节点表示将他入栈,访问一个节点是他处于栈顶,我们即将让他出栈。
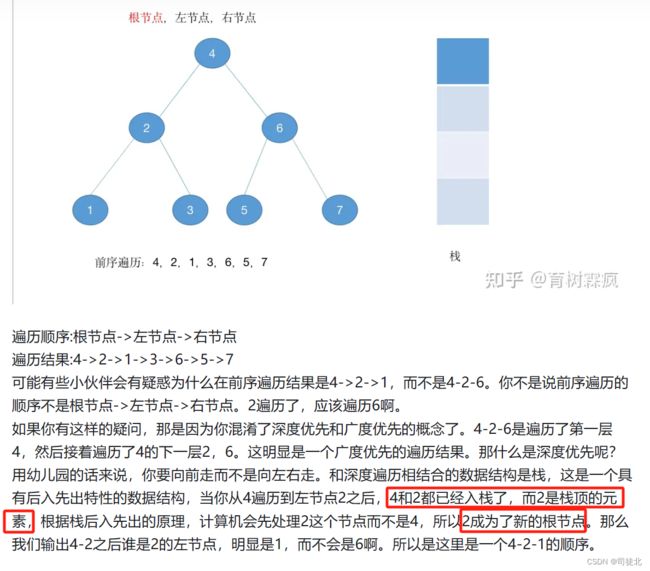
以下内容来自labuladong:https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-66994/dong-ge-da-334dd/#%E6%B7%B1%E5%85%A5%E7%90%86%E8%A7%A3%E5%89%8D%E4%B8%AD%E5%90%8E%E5%BA%8F

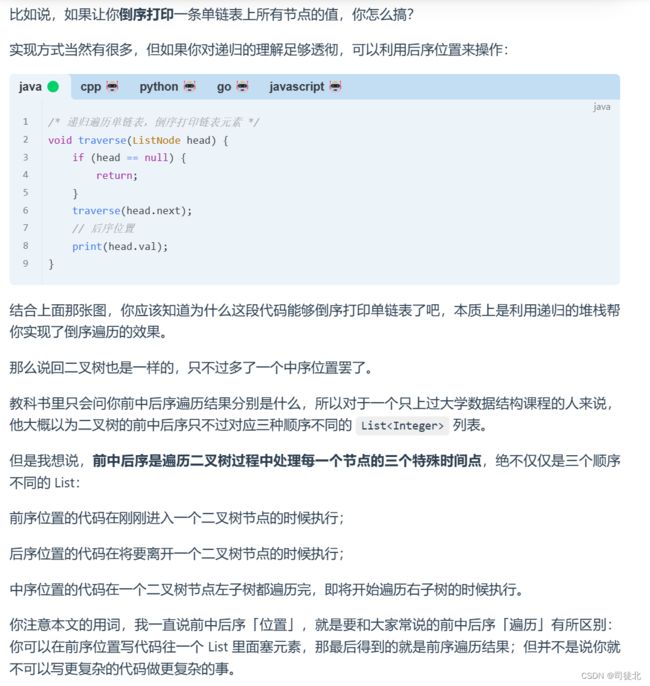
二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的,你只需要单独思考每一个节点应该做什么,其他的不用你管,抛给二叉树遍历框架,递归会在所有节点上做相同的操作。
递归遍历
难点:什么时候记录(访问)本节点的值?
肯定不能写什么 res.add(root.left.val); 因为每个结点我们都能访问到,那么每个结点的值我们也能访问到,就不应该用root.left.val(左节点的值),就应该是res.add(root.val)来记录,只不过是什么时候来记录的问题。
比如下列后序遍历的写法(左右中),意思就是,先遍历左边结点,再遍历右边结点,然后记录当前结点。所以res.add(root.val);放在最后。
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val);
前序
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
preorder(root, res);
return res;
}
public void preorder(TreeNode root, List<Integer> res){
//退出条件
if (root == null){
return;
}
res.add(root.val);
preorder(root.left, res);
preorder(root.right, res);
}
}
中序
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inorder(root, res);
return res;
}
public void inorder(TreeNode root, List<Integer> res){
if (root == null){
return;
}
inorder(root.left, res);
res.add(root.val); // 注意这句
inorder(root.right, res);
}
}
后序
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
postorder(root, res);
return res;
}
public void postorder(TreeNode root, List<Integer> res){
if (root == null){
return;
}
postorder(root.left, res);
postorder(root.right, res);
res.add(root.val); // 注意这句
}
}
迭代遍历
前序
整体的过程就是:先顺着最左边走到底,然后逆着这个顺序不断回退,如果有右树,就进入右树。这个过程其实就是一个先进后出的过程,是符合stack栈的数据结构。
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Stack<TreeNode> stk = new Stack<>();
if (root == null){
return res;
}
stk.push(root);
while (!stk.isEmpty()){
TreeNode cur = stk.pop();
res.add(cur.val);
//要先加入右孩子,再加入左孩子, 因为这样出栈的时候才是中左右的顺序
if (cur.right != null){
stk.push(cur.right);
}
if (cur.left != null) {
stk.push(cur.left);
}
}
return res;
}
}
中序
遇到当前节点,不能立刻遍历,而是需要先在栈中保存,然后顺着最左边不断向下,如果无法向下了,就把栈顶元素取出来,访问栈顶元素,然后转向栈顶元素的右子树。
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Stack<TreeNode> stk = new Stack<>();
//每一个节点都是一个中间节点,哪怕它度为0,那也是左右结点为空的中间节点,所以每次都add一个中间节点是能访问完所有元素的,如果还是不懂,建议画个二叉树跟着走一遍
if (root == null){
return res;
}
TreeNode cur = root;
while (cur != null || !stk.isEmpty()){
if (cur != null){ // 如果当前结点不为空,那就将它压入栈,并移动当前结点为它的左结点
stk.push(cur);
cur = cur.left;
} else{ // 此时当前结点为空(代表栈顶元素的左节点为空,说明左边无法继续向下了,该回到栈顶元素了)
cur = stk.pop();
res.add(cur.val); //访问完当前中间节点了,该访问右边了
cur = cur.right;
}
}
return res;
}
}
后序(后序遍历其实比较麻烦,比较简单的就是改动前序遍历,然后反转了,记住就行)
// 后序遍历顺序 左-右-中 入栈顺序:中-左-右 出栈顺序:中-右-左, 最后翻转结果
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null){
return result;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()){
TreeNode node = stack.pop();
result.add(node.val);
if (node.left != null){
stack.push(node.left);
}
if (node.right != null){
stack.push(node.right);
}
}
Collections.reverse(result);
return result;
}
}
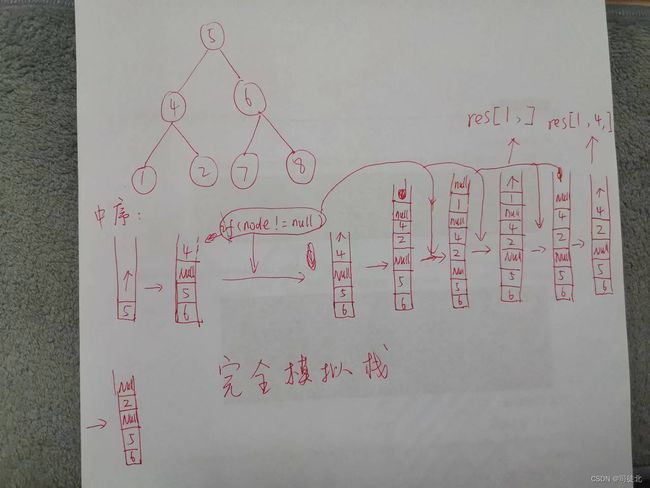
统一版本的迭代法(前中后序几乎不用改代码就能迭代遍历):
!!!!其本质是用显示栈去模拟递归, 这里的模拟是真正做到了完全模拟递归,递归是怎么递归的,栈就是怎么模拟的。 NULL的意思是,该节点刚才已经走过了,这次再遇到它要取出来记录了

class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek(); //创建当前节点 并判断是否访问过
if (node != null) { //非空说明没有访问过,然后右节点入栈,左节点入栈,最后根节点入栈,最后压入一个空节点(重要)
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
//如果弹出的节点为空节点,表明当前栈顶节点已经访问过
st.pop(); // 将空节点弹出
node = st.peek(); // 重新取出栈中元素
st.pop();
result.add(node.val); // 加入到结果集
}
}
return result;
}
}