机器学习算法实战案例：GRU 实现多变量多步光伏预测

1 数据处理

1.1 数据集简介

实验数据集采用数据集7：常州普利司通光伏数据集，包括数据集包括时间、场站名称、辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)等5个特征，时间间隔5min。（注意：辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)特征名前有个空格）

def visualize_data(data, row, col):

    cycol = cycle('bgrcmk')

    cols = list(data.columns)

    fig, axes = plt.subplots(row, col, figsize=(16, 4))

    if row == 1 and col == 1:  # 处理只有1行1列的情况

        axes = [axes]  # 转换为列表，方便统一处理

    for i, ax in enumerate(axes.flat):

        if i < len(cols):

            ax.plot(data.iloc[:,i], c=next(cycol))

            ax.set_title(cols[i])

            ax.axis('off')  # 如果数据列数小于子图数量，关闭多余的子图

    plt.subplots_adjust(hspace=0.5)

visualize_data(data, 1, 3)

​

单独查看部分光伏发电功率数据，发现有较强的规律性。

​

1.2 导入库文件

import matplotlib.pylab as plt

from tensorflow.keras.models import Sequential

from tensorflow.keras.layers import GRU, Dropout, Dense

from sklearn.preprocessing import MinMaxScaler

from sklearn.metrics import mean_squared_error

from itertools import cycle

plt.rcParams['font.sans-serif'] = ['SimHei']     # 显示中文

plt.rcParams['axes.unicode_minus'] = False

plt.rcParams.update({'font.size':18})

1.3 数据集处理

首先检查数据的缺失值情况，通过统计数据可以看到，存在少量缺失值。

时间、场站名称无效信息可以删除，辐照强度(Wh/㎡)、 环境温度(℃)、全场功率(kW)存在少量缺失值，用前后项值进行填充（这里缺失值填充可根据自己的方法处理）。

data.drop(['时间','场站名称'], axis=1, inplace=True)

data = data.fillna(method='ffill')

data = data[[' 辐照强度(Wh/㎡)', ' 环境温度(℃)', ' 全场功率(kW)']]

然后将数据转化为数值类型便于后续处理。

dataf = data.values

1.4 训练数据构造

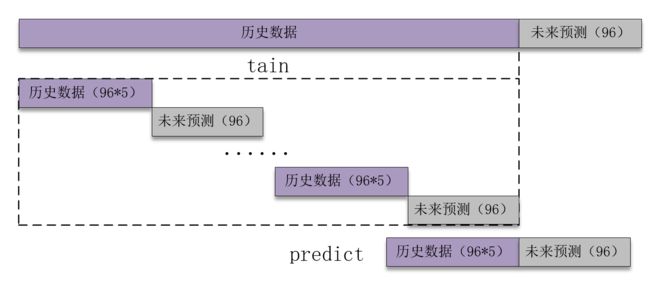
计划预测后1/4天的数据96个，将要预测的数据保留（也就是未来未知的数据），单独提取出前面训练的数据（也就是历史数据），并对数据集进行滚动划分，特征和标签分开划分。

​

def create_dataset(datasetx,datasety,timesteps=36,predict_size=6):

    for each in range(len(datasetx)-timesteps - predict_steps):

        x = datasetx[each:each+timesteps,0:6]

        y = datasety[each+timesteps:each+timesteps+predict_steps,0]

    return datax, datay#np.array(datax),np.array(datay)

接着设置预测的时间步、每次预测的步长、最后总的预测步长，参数可以根据需要更改。跟前面文章不同的是，这里没有滚动预测，因为没有持续的特征传入，在实际运用有特征传入时可以滚动预测。

timesteps = 96*5 #构造x，为96*5个数据,表示每次用前5/4天的数据作为一段

predict_steps = 96 #构造y，为96个数据，表示用后1/4的数据作为一段

length = 96 #预测多步，预测96个数据据

接着对数据进行归一化处理，特征和标签分开划分，并分开进行归一化处理。

datafy = dataf[:,-1].reshape(dataf.shape[0],1)

scaler1 = MinMaxScaler(feature_range=(0,1))

scaler2 = MinMaxScaler(feature_range=(0,1))

datafx = scaler1.fit_transform(datafx)

datafy = scaler2.fit_transform(datafy)

最后对这行数据集进行划分，并将数据变换为满足模型格式要求的数据。

trainx, trainy = create_dataset(datafx[:-predict_steps*6,:],datafy[:-predict_steps*6],timesteps, predict_steps)

trainx = np.array(trainx)

trainy = np.array(trainy)

2 模型训练与预测

2.1 模型训练

首先搭建模型的常规操作，然后使用训练数据trainx和trainy进行训练，进行20个epochs的训练，每个batch包含128个样本。此时input_shape划分数据集时每个x的形状。（建议使用GPU进行训练，因为本人电脑性能有限，建议增加epochs值）

physical_devices = tf.config.list_physical_devices('GPU')

tf.config.experimental.set_memory_growth(physical_devices[0], True)

start_time = datetime.datetime.now()

model.add(GRU(128, input_shape=(timesteps, trainx.shape[2]), return_sequences=True))

model.add(GRU(64, return_sequences=False))

model.add(Dense(predict_steps))

model.compile(loss="mean_squared_error", optimizer="adam")

model.fit(trainx, trainy, epochs=20, batch_size=128)

end_time = datetime.datetime.now()

running_time = end_time - start_time

model.save('gru_model.h5')

2.2 模型多步预测

下面介绍文章中最重要，也是真正没有未来特征的情况下预测未来标签的方法。整体的思路也就是，前面通过前96*5个数据训练后面的96个未来数据，预测时取出前96*5个数据预测未来的96个未来数据。这里与单变量预测不同，没有进行滚动预测，因为单变量预测的结果可以作为历史数据进行滚动，这里多变量只产生了预测值，并没有预测标签，不能进行滚动预测，在实际有数据源源不断时可以采用滚动预测。（里面的数据可以根据需求进行更改）

​首先提取需要带入模型的数据，也就是预测前的96*5行特征和后96个标签。

然后加载训练好的模型：

2.3 预测可视化

预测并计算误差，并进行可视化，将这些步骤封装为函数。

def predict_and_plot(x, y_true, model, scaler, timesteps):

    predict_x = np.reshape(x, (1, timesteps, 2))  

    predict_y = model.predict(predict_x)

    predict_y = scaler.inverse_transform(predict_y)

    y_predict.extend(predict_y[0])

    train_score = np.sqrt(mean_squared_error(y_true, y_predict))

    print("train score RMSE: %.2f" % train_score)

    cycol = cycle('bgrcmk')

    plt.plot(y_true, c=next(cycol), markevery=5)

    plt.plot(y_predict, c=next(cycol), markevery=5)

    plt.legend(['y_true', 'y_predict'])

最后运行结果，发现预测的效果大致捕捉了趋势，预测值存在一定程度的波动，也出现功率值小于0的情况，可以自行处理。

y_predict = predict_and_plot(predictx1, y_true1, model, scaler2, timesteps)

答疑&技术交流

技术要学会分享、交流，不建议闭门造车。一个人可以走的很快、一堆人可以走的更远。

本文完整代码、相关资料、技术交流&答疑，均可加我们的交流群获取，群友已超过2000人，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友。

​方式①、微信搜索公众号：Python学习与数据挖掘，后台回复：加群
方式②、添加微信号：dkl88194，备注：来自CSDN + 技术交流

机器学习算法实战案例系列

• 机器学习算法实战案例：确实可以封神了，时间序列预测算法最全总结！

• 机器学习算法实战案例：时间序列数据最全的预处理方法总结