leetcode

代码随想录计划

Day 23–回溯算法

组合总和

组合总和

这个和之前的组合系列都是类似的，唯一要注意的就是这里的元素可以重复使用。本来以为不需要 start 来标注开始位置了，不过没有start标注位置会出现重复的组合所以仍然需要。

本题还需要startIndex来控制for循环的起始位置，对于组合问题，什么时候需要startIndex呢？

举过例子，如果是一个集合来求组合的话，就需要start Index

如果是多个集合取组合，各个集合之间相互不影响，那么就不用start Index

class Solution {
    private List<List<Integer>> result;
    private List<Integer> list;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        result = new LinkedList<>();
        list = new LinkedList<>();
        backtracking(candidates,target,0);
        return result;
    }

    public void backtracking(int[] candidates,int target,int start){
        if(target == 0){
            result.add(new LinkedList(list));
            return;
        }
        for(int i = start;i<candidates.length;i++){
            if(target-candidates[i]<0) break;
            list.add(candidates[i]);
            backtracking(candidates,target-candidates[i],i);
            list.remove(list.size()-1);
        }
    }
}

if(target-candidates[i]<0) break;这句是为了剪枝操作。

组合总和 II

组合总和 II

本题的难点在于：集合（数组candidates）有重复元素，但还不能有重复的组合。代码随想录 (programmercarl.com)

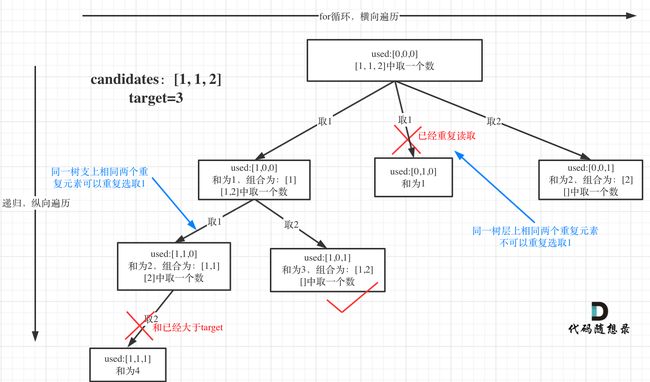
我们从回溯树中分析：

在深度的遍历中，数组中的重复元素是可以重复选用的，就比如，数组中有两个1，为了凑成target == 2是可以使用的。这是两个元素只不过是值相同。

在宽度遍历中，由于1是重复的，我们前面以及深度递归过1这个元素，后面还有1的话我们再次深度遍历1这个元素势必会和前面出现过的组合重复。所以我们要做的是在宽度遍历时去重。

这里去重的方法：

1.对数组排序 ，对数组排序这个操作是必须的，这样才能够将重复的元素相邻在一起才能判断。不然无法知道重复的元素两个的坐标关系。

2.判断该元素之前是否深度遍历过。 这个方法有两种，一个是用一个 used数组来标记是否使用过，一个是使用start 标记开始位置的变量来判断。具体看代码

使用used数组：这里i>0 && candidates[i] == candidates[i-1]&&used[i-1] == false 其实就是标记这次循环是深度还是宽度。当为false的时候为宽度时的for循环需要去重

class Solution {
    private List<List<Integer>> result;
    private List<Integer> list;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        result = new LinkedList<>();
        list = new LinkedList<>();
        Arrays.sort(candidates);
        boolean[] used = new boolean[candidates.length];
        backtracking(candidates,target,0,used);
        return result;
    }
    public void backtracking(int[] candidates,int target,int start,boolean[] used){
        if(target < 0 ) return;
        if(target == 0){
            result.add(new LinkedList<>(list));
            return;
        }
        for(int i = start;i<candidates.length;i++){
            if(i>0 && candidates[i] == candidates[i-1]&&used[i-1] == false) continue;
            list.add(candidates[i]);
            used[i] = true;
            backtracking(candidates,target - candidates[i],i+1,used);
            list.remove(list.size() -1 );
            used[i] = false;
        }
    }
}

不适用used数组：这里的去重体现在这里if(i>start && candidates[i] == candidates[i-1]) continue;由于每次深度遍历时，start都是i+1 而排序后相同元素又相邻，所以在深度遍历时，一开始i>start是永远无法满足的，这样对取重复值就不会有影响。而在宽度时，由于start此时对同一宽度的情况下是一样的，i>start就排除了使用相同元素深度遍历的情况。

class Solution {
    private List<List<Integer>> result;
    private List<Integer> list;
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        result = new LinkedList<>();
        list = new LinkedList<>();
        Arrays.sort(candidates);
        backtracking(candidates,target,0);
        return result;
    }
    public void backtracking(int[] candidates,int target,int start){
        if(target < 0 ) return;
        if(target == 0){
            result.add(new LinkedList<>(list));
            return;
        }
        for(int i = start;i<candidates.length;i++){
            if(i>start && candidates[i] == candidates[i-1]) continue;
            list.add(candidates[i]);
            backtracking(candidates,target - candidates[i],i+1);
            list.remove(list.size() -1 );
        }
    }
}

分割回文串

这题就算一开始知道要用回溯写，也比较难写。

具体遇到的问题：

• 如何进行字符串的分割
• 切割问题中递归如何终止
• 对字符串是否为回文串的判断
• 判断子串后的处理

一下子想出来每个点是不容易的

具体看看题解或者视频

代码随想录 (programmercarl.com)

带你学透回溯算法-分割回文串（对应力扣题目：131.分割回文串）| 回溯法精讲！_哔哩哔哩_bilibili

class Solution {
    List<List<String>> result;
    List<String> list;
    public List<List<String>> partition(String s) {
        result = new LinkedList<>();
        list = new LinkedList<>();
        backtracking(s,0);
        return result;
    }
    public void backtracking(String s,int startIndex){
        if(startIndex >= s.length()){
            result.add(new LinkedList<>(list));
            return;
        }
        for(int i = startIndex; i<s.length();i++){
            if(isPolindrome(s,startIndex,i)){
                list.add(s.substring(startIndex,i+1));
            }else continue;
            backtracking(s,i+1);
            list.remove(list.size()-1);
        }

    }

    public boolean isPolindrome(String s,int start ,int end){
        while(start < end){
            if(s.charAt(start) != s.charAt(end)) return false;
            start++;
            end--;
        }
        return true;
    }
}

剩下的优化就在于如何让判断子串是否为回文串更加高效，学有余力可以进行。