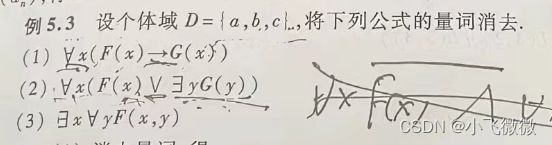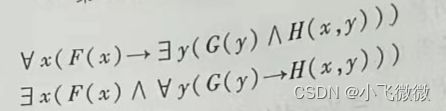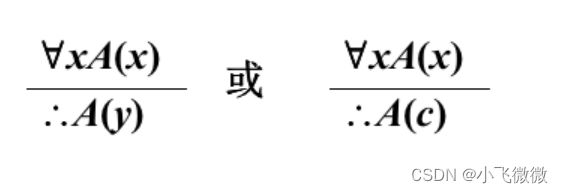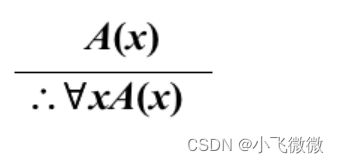离散数学（屈婉玲）一阶逻辑等值演算与推理

前言

这节知识点比较重要吼，期末考试老喜欢考了~~

这个我尽量写的更加详细一点~

好好学哈

---

一阶逻辑等值式与置换规则

先引入定义等值式：

设A，B是一阶逻辑中任意两个任意公式，若A<->B是永真式，则称A与B等值，记作A <=>B.称A<=>B是等值式。

由定义可知，判断公式A与B是否等值，等价于判断公式A与B是否为永真式

同命题逻辑中一样，证明了一些常用的重要等值式，并用这些等值式推演出更多的等值式，这就是一阶逻辑等值演算的内容.

举个栗子：

 ∀xF(x)<=>¬¬∀xF(x)
 ∀x∃y(F(x,y)->G(x,y))<=>¬¬∀x∃y(F(x,y)->G(x,y))

 

量词否定等值式：

可以如下直观解释

对于(1)“并不是所有的 都有性质 A”与“存在 没有性质 A”是一回事.

对于(2)，“不存在有性质A 的”与“所有 都没有性质 A”是一回事

量词辖域收缩与扩张等值式

这部分等值式非常重要，并且使用时要求符合成立条件，即“A(x)是含自由变量x的公式、并且x不在B中出现”

量词分配等值式

进行等值演算,除以上基本等值式外,还有以下2 条规则:

1). 置换规则：

设Φ(A)是含A的公式, 那么, 若A⇔B, 则Φ(A)⇔Φ(B).

2). 换名规则
设A为一公式，将A中某量词辖域中个体变项的所有约束
出现及相应的指导变元换成该量词辖域中未曾出现过的个
体变项符号，其余部分不变，设所得公式为A’，则A’⇔A.

举个栗子 ：

将下而公式化成等值的公式,使其不含既是约束出现又是自由出现的个体变项

.(1) ∀xF(x,y,z)一>∃yG(x,y,z)

(2)  ∀x(F(x,y)一>∃yG(x,y,z))

解：

(1) 公式中x,y 都是既约束出现,又自由出现的个体变项,可以通过换名消去这种情况

∀xF(x,y,z)一>∃yG(x,y,z)

<=>∀tF(t,y,z)一>∃yG(x,y,z)      (换名规则)

<=>∀tF(t,y,z)一>∃wG(x,w,z)     (换名规则)

(2)公式中y既有约束出现,又有自由出现,需要处理.而x 只有约束出现，z只有自由出现,保持不变.
∀x(F(x,y)一>∃yG(x,y,z))
<=>∀x(F(x,y)一>∃tG(x,t,z))        (换名规则)

再举个栗子：

证  (1) 取A(x)= F(x),B(x)= G(x),并证明∀x(F(x)VG(x)) <->∀xF(x)V ∀xG(x)不
是永真式

,其中 F(x)和 G(x)是谓词变项.

取解释1为:

个体域为自然数集合 N,F(x):x 是奇数,G(x): 是偶数,则∀x(F(x)VG(x)) 在解释1下为真命题,而∀xF(x)V ∀xG(x)为假命题.故∀x(F(x)VG(x)) <->∀xF(x)V ∀xG(x)不是永真式.

可以类似地证明(2).

在看一道不错的好题：

解：

   （1）：

消去量词：

(F(a)->G(a))∧(F(b)->G(b))∧(F(c)-G(c))

剩下的如图：

---

一阶逻辑前束范式

例如：

∀x∀y(F(x)∧G(y)->H(x,y))
∀x∀y∃z(F(x)∧G(y)∧H(z)->L(x,z))等都是前束范式

但是

不是！！！

前束范式要求的是所有量词都要在最外面！！！

举些栗子：

注意:
1.在(1)中使用∀对∧的分配律,得到只带一个量词的前束范式

2.∀对V不适合分配律,在(2)中要使用辖域扩张式(5.2)的第一式。

为此需通过换名使得V前后两项中的指导变元不重名.使用式(5.3)时也与此类似.

---

 一阶逻辑的推论理论

大白话就是：给你条件A1，A2...Ak

利用这么多条件给证明B；

能证明出来就称推理正确；

否则：推理不正确

推理定理就是：永真式的蕴含式

一些常用的重要的推理定律：

量词消去引入规则

1. 全称量词消去规则（∀-）

其中x,y是个体变项符号, c是个体常项符号, 且在A中x不在∀y
和 ∃y的辖域内自由出现.

2.全称量词引入规则(∀+)

其中x是个体变项符号, 且不在前提的任何公式中自由出现

3.存在量词消去规则( ∃-)

其中x是个体变项符号, 且不在前提的任何公式和B中自由
出现

4.存在量词引入消去规则(∃+)

其中x,y是个体变项符号, c是个体常项符号, 且在A中y和c不在
∀x和∃x的辖域内自由出现.

---

 自然推理系统NL 定义如下:

1. 字母表. 同一阶语言L的字母表
2. 合式公式. 同L 的合式公式

     3.推理规则:
(1) 前提引入规则
(2) 结论引入规则
(3) 置换规则
(4) 假言推理规则
(5) 附加规则
(6) 化简规则
(7) 拒取式规则
(8) 假言三段论规则
(9) 析取三段论规则
(10) 构造性二难推理规则
(11) 合取引入规则
(12) ∀-规则
(13) ∀+规则
(14) ∃-规则
(15) ∃+规则
要特别注意使用∀-、∀+、∃-、∃+规则的条件

再来一些栗子：

---

一阶逻辑知识点到此就全部分享结束啦~~

如果哪里写错了，或者对于某个知识点有更好的理解，欢迎在评论区留言吼~

谢谢大家哈~