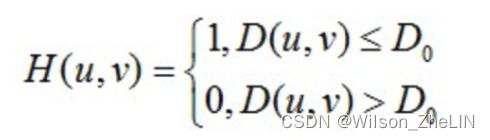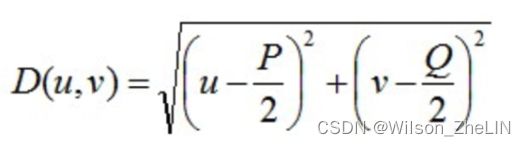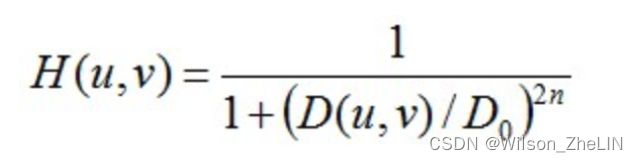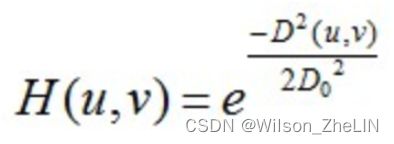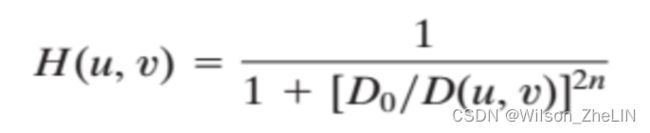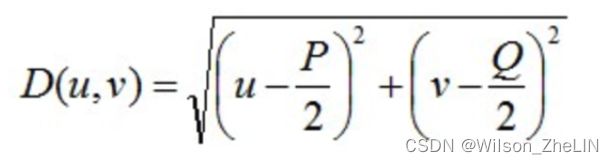C语言数字图像处理（六）：低通滤波器和高通滤波器
0. 完整仓库&教程：
这一章节的完整代码在：Chapter 6. Low Pass Filter and High Pass Filter
如果你喜欢这个系列的文章或者感觉对你有帮助，请给我的仓库一个⭐️。
1. 低通滤波器
-
1.1 理想低通滤波器（Ideal Low Pass Filter）
算法：
首先对图像进行二维离散傅里叶变换（这部分的原理可以参考：离散傅里叶变换和重建），得到每个像素的复数数组。 每个复数的实部和虚部分别乘以 (, )。 (, ) 的公式为：
其中 
代表通带(passband)的半径。(, )的计算方法是通过以下公式计算两点之间的距离:
其中， 和 是图像的长和宽。 最后，使用二维离散傅里叶逆变换（iDFT）恢复处理后的图像。
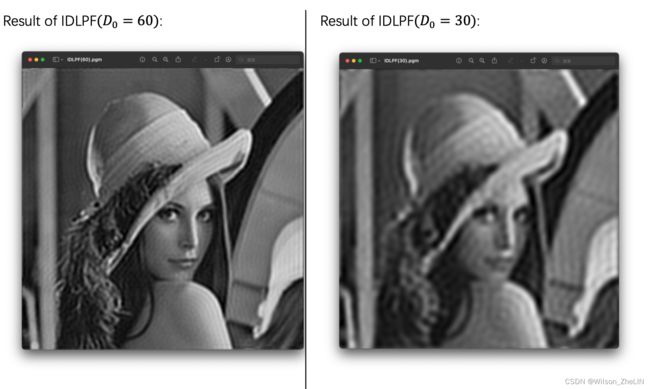
图像和结果对比（lena）：
结果分析：
理想的低通滤波器可以完全抑制所有高于截止频率的频率信号，而低于截止频率的信号可以不受影响地通过。 由于理想低通滤波器的过渡特性过于尖锐，因此会出现振铃现象（ringing）。 它滤除了图像的高频部分，从而使图像变得模糊。 另外， 选择的值越小，图像处理的效果越明显，即越模糊。
代码：
void IDLPF(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float height = image->Height, width = image->Width;
float real[(int)(height*width)], imaginary[(int)(height*width)];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
int H;
if(dis <= 60) H = 1;
else H = 0;
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("IDLPF Finished!\n");
outimage = iDFT(image, real, imaginary);
SavePNMImage(outimage, (char*)"IDLPF.pgm");
}1.2 巴特沃斯低通滤波器（Butterworth Low Pass Filter）：
算法：
与上面 IDLFT 相比唯一的区别是它改变了 (, ) 的公式：
其中 是巴特沃斯滤波器的阶数。
图像和结果对比（lena）：
结果分析：
根据巴特沃斯滤波器的特性，在通带（pass band）内频率响应曲线是平坦的、无纹波，且在阻带（stop band）内逐渐降至零。 因此它处理的图像明显比上面的IDLPF 更自然、更平滑。 选择的 值越小，图像会越模糊。不过随着次数的增加，振铃现象会变得更加明显。
代码实现(完整代码见顶部GitHub)：
void BLPF(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float height = image->Height, width = image->Width;
float real[(int)(height*width)], imaginary[(int)(height*width)];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H = 1 / (1 + pow(dis / (float)60, 2));
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("BLPF Finished!\n");
outimage = iDFT(image, real, imaginary);
SavePNMImage(outimage, (char*)"BLPF.pgm");
}1.3 高斯低通滤波器（Gaussian Low Pass Filter）：
算法：
高斯低通滤波器中，(, )的公式为：
其他部分与之前的算法相同。
图像和结果对比（lena）：
结果分析：
高斯滤波器的过渡特性非常平坦，因此即使非常小，也不会出现振铃现象。处理后的图像非常平滑，选择较小的值会导致图像更加模糊。此外，这个算法也可适用于去除图像噪音和背景模糊。
代码实现(完整代码见顶部GitHub)：
void GLPF(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float height = image->Height, width = image->Width;
float real[(int)(height*width)], imaginary[(int)(height*width)];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H = pow(M_E, pow(dis, 2) * -1 / (pow(60, 2) * 2));
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("GLPF Finished!\n");
outimage = iDFT(image, real, imaginary);
SavePNMImage(outimage, (char*)"GLPF.pgm");
}2. 高通滤波器
算法：
首先对图像进行DFT变换，得到每个像素的复数数组。 每个复数的实部和虚部分别乘以 (, )。 (,)的公式如下（为了图像锐化的效果，这里选择巴特沃斯低通滤波器）：
其中表示通带的半径。 (, )的计算方法也是两点之间的距离，通过公式：
其中， 和 是图像的长和宽。 最后，使用iDFT恢复处理后的图像。
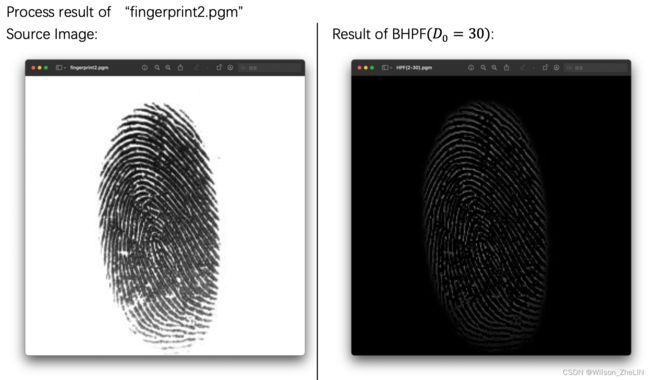
图像和结果对比（fingerprint1, fingerprint2）：
结果分析：
为了获得更明显的锐化效果这里选择了巴特沃斯高通滤波器。 从输出结果可以看出，高频值被去除，低频值被保留，因此指纹的边缘被锐化并突出显示。 的值越低，图像处理的效果越明显。
代码实现(完整代码见顶部GitHub)：
void HPF(Image *image, float *real_array, float *imaginary_array) {
unsigned char *tempin, *tempout;
float height = image->Height, width = image->Width;
float real[(int)(height*width)], imaginary[(int)(height*width)];
Image *outimage;
outimage = CreateNewImage(image, (char*)"#testing function");
tempin = image->data;
tempout = outimage->data;
for(int i = 0; i < height; i++) {
for(int j = 0; j < width; j++) {
float dis = sqrt(pow((float)i - height/2, 2) + pow((float)j - width/2, 2));
float H = 1 / (1 + pow((float)30 / dis, 2));
real[(int)(i*height + j)] = real_array[(int)(i*height + j)] * H;
imaginary[(int)(i*height + j)] = imaginary_array[(int)(i*height + j)] * H;
}
}
printf("HPF Finished!\n");
outimage = iDFT(image, real, imaginary);
SavePNMImage(outimage, (char*)"HPF.pgm");
}3. 完整代码
这一章节的完整代码在：Chapter 6. Low Pass Filter and High Pass Filter
更多关于数字图像处理的章节，以及所有的原图像在：Introduction to Digital Image Processing
整理代码、翻译原理，和可视化每一个章节的工作非常耗时耗力，并且不会有任何收入和回报。如果你喜欢这个系列的文章或者感觉对你有帮助，请给我的仓库一个⭐️，这将是对独立作者最大的鼓励。
-END-