基于决策树的规则挖掘实战分析,值得细嚼慢咽
今天,为大家分享基于决策树算法的风控规则挖掘实战分析哦。
基于决策树挖掘风控规则实战分析
决策树算法
1.来源背景
决策树算法最早于20世纪60年代提出,由于其直观易懂的特点,迅速成为人们研究和解决决策问题的重要工具。随着机器学习的发展,决策树算法逐渐演化为一种强大的预测和分类方法。其中,CART算法作为决策树算法的重要分支,于1984年由Breiman等人提出,以其出色的性能和灵活的应用而受到广泛关注。
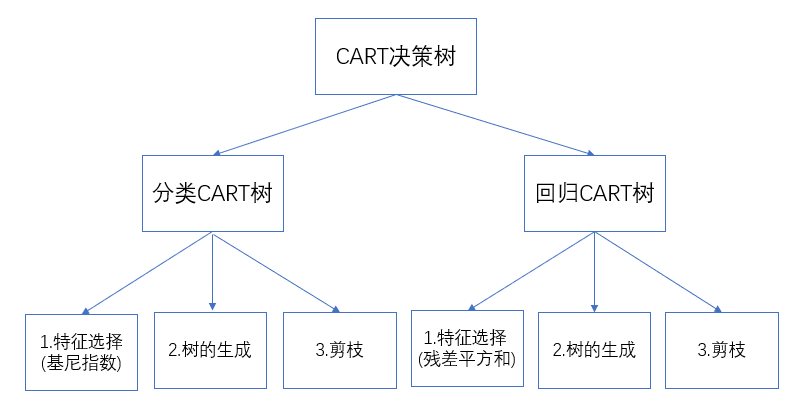
2.CART算法
CART(Classification And Regression Tree)算法是一种基于GINI系数的决策树算法。它通过计算GINI系数来度量节点的纯度,进而选择最佳的切分点将样本划分为不同的子集。CART算法在构建决策树时,采用贪心策略,以最小化GINI系数的变化作为判断标准,逐步构建出一个优化的决策树模型。此外,CART算法还支持分类问题和回归问题,使其具备更广泛的应用。
3.应用场景和优势
CART算法在各个领域有着广泛的应用。在金融领域,CART算法可以帮助银行和保险公司进行客户信用评估和风险预测;在医疗领域,CART算法可用于疾病诊断和药物反应预测;在市场营销中,CART算法可用于用户分类和推荐系统等。相比其他算法,CART算法具有简单易懂、计算效率高、可解释性强等优势,因此备受青睐。
4.决策树算法逻辑
对于分类问题,CART算法使用GINI系数来度量一个节点的纯度。GINI系数衡量了从一个数据集中随机选择两个样本,这两个样本属于不同类别的概率。具体而言,对于一个节点上的样本集合,其GINI系数的计算公式如下:
GINI(p) = 1 - Σ(pi^2)
其中,p是节点上每个类别的概率,pi表示某个特定类别的概率。
在构建CART决策树时,算法会根据GINI系数的变化选择最佳的切分点,将样本分为不同的子集。这个过程会递归地进行,直到满足某个停止条件,例如树的深度达到一定的限制或节点上的样本数量小于某个阈值。最终构建出的CART决策树可以用于做分类或回归。
需要注意的是,CART算法可以用于分类问题和回归问题。在分类问题中,每个叶节点代表一个类别;而在回归问题中,每个叶节点代表一个数值。因此,CART算法是一种灵活且广泛应用于各种场景的决策树算法。
5.决策树剪枝
训练集中预测值和真实值越接近说明拟合效果越好,但是有时数据过度地拟合训练数据,导致模型的泛化能力较差,在测试数据中的表现并不好。
为了防止模型发生过拟合,可以对“完全生长”的CART树底端剪去一些枝,使得决策树变小从而变得简单。
其实剪枝分为预剪枝和后剪枝,预剪枝是在构建决策树的过程中,提前终止决策树的生长,从而避免过多的节点产生。但是由于很难精确判断何时终止树的生长,导致预剪枝方法虽然简单但实用性不强。
后剪枝是在决策树构建完成之后,通过比较节点子树用叶子结点代替后的误差大小,如果叶子结点合并后误差小于合并前,则进行剪枝,否则不剪枝。
挖掘规则逻辑
CART决策树的构建是一个递归过程,可以大致分为以下几个步骤:
1. 数据准备:
- 收集数据:确保数据集中包含目标变量和预测变量。
- 数据清洗:处理缺失值、异常值,可能需要进行数据转换或编码。
2. 特征选择:
- 对于每一个节点,计算每个特征的最佳分割点,这通常根据GINI指数或均方误差(回归树的情况下)来确定。
- 选择具有最小GINI指数(分类)或最小均方误差(回归)的特征和对应的分割点。
3. 树的构建:
- 使用上一步找到的最佳分割点,将数据分为两个子集。
- 对每个子集递归执行步骤2,继续分割,直至满足停止条件。
- 停止条件包括:达到最大深度、节点中的样本数量少于最小分割所需样本量、节点的纯度(GINI指数或均方误差)已经足够低或其他自定义条件。
4. 剪枝:
- 树构建完成后,可能会进行剪枝操作以避免过拟合。
- 剪枝包括预剪枝(在构建过程中提前停止树的增长)和后剪枝(在树构建完成后去除一些分支)。
- 选择最优的剪枝参数(如最小的成本复杂度剪枝)以提高模型的泛化能力。
5. 模型评估:
- 在独立的测试集上评估模型的性能。
- 使用适当的评估指标,如准确率、召回率、ROC曲线、均方误差等来评估分类或回归树的表现。
6. 使用模型:
- 将评估合格的模型应用于实际的分类或回归问题中。
- 决策树模型可以直接对新的数据样本做出预测。
这个过程可以通过机器学习库(如Python的scikit-learn)中的CART实现自动完成。模型构建后,你可以使用各种方法对决策树进行可视化,直观了解模型的决策路径。
7.cart树每个treenode存储了哪些数据?
在CART决策树中,每个节点(TreeNode)通常存储以下数据:
-
划分特征:这是用于根据某种条件划分数据集的特征。例如,如果一个节点用"年龄 > 30"作为分割条件,那么"年龄"就是这个节点的划分特征。
-
划分阈值:与划分特征配合使用,定义了数据应如何分割。在上面的例子中,阈值是30。
-
左子节点:满足划分条件的数据子集的节点。例如,在上面的"年龄 > 30"例子中,大于30岁的数据会被划分到左子节点。
-
右子节点:不满足划分条件的数据子集的节点。在上面的例子中,30岁及以下的数据会被划分到右子节点。
-
类标签:只在叶节点中有效。表示该节点所代表的数据子集中最常见的类别。当新数据通过决策树进行预测时,最终到达的叶节点的类标签就是其预测结果。
-
数据子集:节点当前代表的数据子集。在许多实际实现中,为了节省内存,节点可能不直接存储数据子集,而是存储数据索引或其他引用。
-
基尼不纯度或其他不纯度指标:代表当前数据子集的不纯度。在构建树的过程中,这个指标用于判断是否应该继续划分当前节点。
-
其他可选信息:如节点深度、父节点引用、数据点的数量等。
8.决策树算法
```python
# 导入所需的库
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# 读取数据
data = pd.read_csv('credit_data.csv') # 假设数据保存在名为credit_data.csv的文件中
# 数据预处理
# 对于决策树算法,需要将文本数据转换为数字数据
data['income'] = data['income'].map({'high': 1, 'low': 0})
data['age'] = data['age'].map({'young': 0, 'middle-aged': 1, 'senior': 2})
# 划分特征和标签
X = data.drop('default', axis=1)
y = data['default']
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建决策树模型
model = DecisionTreeClassifier()
# 在训练集上拟合模型
model.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = model.predict(X_test)
# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("准确率:", accuracy)
```9.决策树参数介绍
在Python中,使用`scikit-learn`库的`DecisionTreeClassifier`或`DecisionTreeRegressor`类可以实现基于分类和回归树(CART)算法的决策树。这些类的关键参数如下:
### DecisionTreeClassifier
1. `criterion`: 用来测量分割质量的函数。对于分类树,默认是`'gini'`(基尼不纯度),也可以选择`'entropy'`(信息增益)。
2. `splitter`: 用于在节点分割时选择最优分割策略的方法。默认是`'best'`,表示选择最优分割,也可以设置为`'random'`随机分割。
3. `max_depth`: 树的最大深度。如果没有设置,那么节点会扩展直到所有叶子节点都是纯净的(所有的样本都属于同一个类),或者包含的样本数小于`min_samples_split`。
4. `min_samples_split`: 分割一个节点需要的最小样本数,默认是2。
5. `min_samples_leaf`:
一个叶子节点需要包含的最小样本数,默认是1。
6. `max_features`: 分割节点时考虑的最大特征数。可以设置为整数、浮点数、字符串或者`None`。默认是`None`,表示考虑所有的特征。
7. `random_state`: 控制算法随机状态的整数。可以用于确保多次运行的可复现性。
8. `max_leaf_nodes`: 最大叶子节点数量,如果设置了这个参数,那么`max_depth`将会被忽略。
这些参数对于避免过拟合、优化计算效率和决策树的性能都非常关键。
### DecisionTreeRegressor
回归决策树`DecisionTreeRegressor`的参数和分类决策树`DecisionTreeClassifier`大体相同,不同之处在于回归树的默认`criterion`是`'squared_error'`,表示使用均方差分割;其他参数功能与分类树保持一致。
这些参数允许对决策树的训练和结构进行细粒度的控制,但同时也需要注意,不合理的参数设置可能会导致模型过拟合或者欠拟合。通常需要通过交叉验证来选择最合适的参数。
风控实战代码
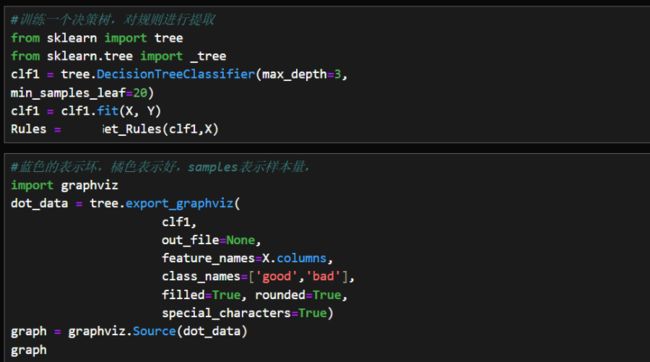
调用sklearn中的决策树回归模型,设定树的最大深度为2层。将x作为挖掘变量,将creditability作为y标签。使用graphviz对输出结果进行可视化展示。
可视化
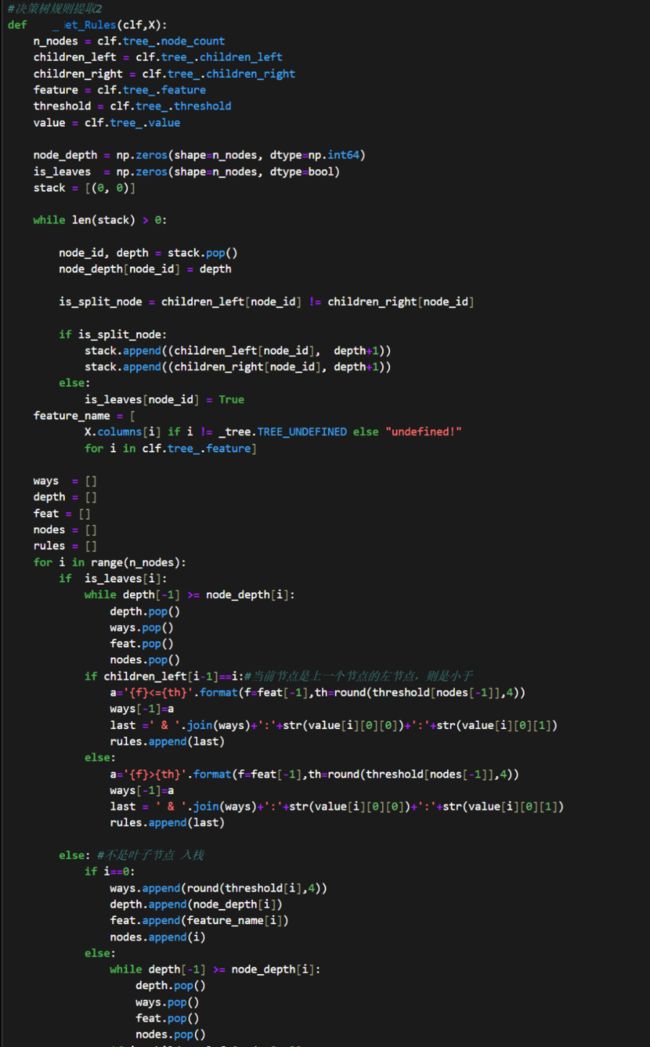
规则生成