基于协方差矩阵自适应演化策略(CMA-ES)的高效特征选择
特征选择是指从原始特征集中选择一部分特征,以提高模型性能、减少计算开销或改善模型的解释性。特征选择的目标是找到对目标变量预测最具信息量的特征,同时减少不必要的特征。这有助于防止过拟合、提高模型的泛化能力,并且可以减少训练和推理的计算成本。
如果特征N的数量很小,那么穷举搜索可能是可行的:比如说尝试所有可能的特征组合,只保留成本/目标函数最小的那一个。但是如果N很大,那么穷举搜索肯定是不可能的。因为对于N的组合是一个指数函数,所以在这种情况下,必须使用启发式方法:以一种有效的方式探索搜索空间,寻找能够最小化用于执行搜索的目标函数的特征组合。
找到一个好的启发式算法并非易事。R中的regsubsets()函数有一些可以使用的选项。此外,scikit-learn提供了几种执行启发式特征选择的方法,但是找到一个好的、通用的启发式——以最通用的形式——是一个难题。所以本文将探讨一些即使在N相当大的情况下也能很好地工作的方法。
数据集
我们这里使用Kaggle上非常流行的House Prices数据集(MIT许可)——然后经过一些简单的特征转换后,最终得到一个213个特征(N=213)和1453个观察值的数据集。我使用的模型是线性回归,statsmodels.api.OLS(),我们试图最小化的目标函数是BIC,贝叶斯信息标准,一种信息损失的度量,所以BIC越低越好。它与AIC相似,只不过BIC倾向于生成更简洁的模型(它更喜欢特征较少的模型)。最小化AIC或BIC可以减少过拟合。但也可以使用其他目标函数,例如r方(目标中已解释的方差)或调整后的r方——只要记住r平方越大越好,所以这是一个最大化问题。
目标函数的选择在这里是无关紧要的。重要的是我们要有一个目标函数,因为需要尝试使用各种技术来优化它。
但首先,让我们看看一些众所周知的、久经考验的特征选择技术,我们将使用它与后面描述的更复杂的技术进行基线比较。
顺序特征搜索 SFS
SFS相当简单,它从选择一个特征开始,然后选择使目标函数最小的特征。一旦一个特性被选中,它就会永远被选中。然后它会尝试添加另一个特征(这时就有2个了),然后再次最小化目标。当所有特征一起被尝试时,搜索就结束了,使目标最小化的组合最为特征选择的结果。
SFS是一种贪婪算法——每个选择都是局部最优的——而且它永远不会回去纠正自己的错误。但他有一个优点就是即使N很大,它还是很快的。它尝试的组合总数是N(N+1)/2,这是一个二次多项式。
在Python中使用mlextend库的SFS代码是这样的
import statsmodels.api as sm
from mlxtend.feature_selection import SequentialFeatureSelector as SFS
from sklearn.base import BaseEstimator
class DummyEstimator(BaseEstimator):
# mlxtend wants to use an sklearn estimator, which is not needed here
# (statsmodels OLS is used instead)
# create a dummy estimator to pacify mlxtend
def fit(self, X, y=None, **kwargs):
return self
def neg_bic(m, X, y):
# objective function
lin_mod_res = sm.OLS(y, X, hasconst=True).fit()
return -lin_mod_res.bic
seq_selector = SFS(
DummyEstimator(),
k_features=(1, X.shape[1]),
forward=True,
floating=False,
scoring=neg_bic,
cv=None,
n_jobs=-1,
verbose=0,
# make sure the intercept is not dropped
fixed_features=['const'],
)
n_features = X.shape[1] - 1
objective_runs_sfs = round(n_features * (n_features + 1) / 2)
t_start_seq = time.time()
# mlxtend will mess with your dataframes if you don't .copy()
seq_res = seq_selector.fit(X.copy(), y.copy())
t_end_seq = time.time()
run_time_seq = t_end_seq - t_start_seq
seq_metrics = seq_res.get_metric_dict()
它快速找到了这些组合:
best k: 36
best objective: 33708.98602877906
R2 @ best k: 0.9075677543649224
objective runs: 22791
total run time: 44.850 sec
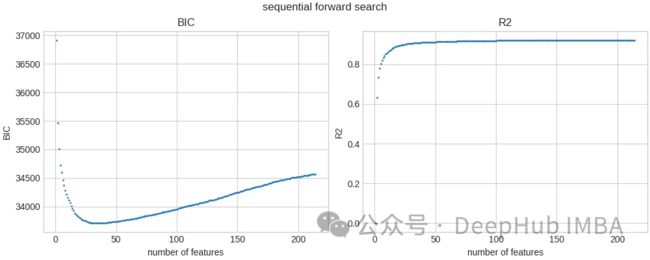
213个特征,最好的是36个。最好的BIC是33708.986,在我的系统上完成不到1分钟。它调用目标函数22.8k次。
以下是最佳BIC值和r平方值,作为所选特征数量的函数:
现在我们来试试更复杂的。
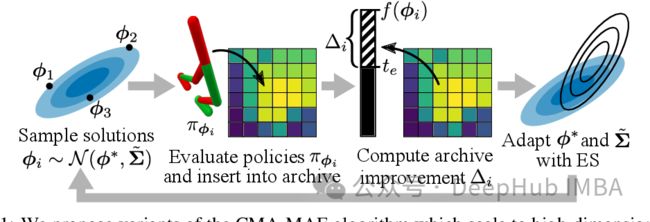
协方差矩阵自适应演化 CMA-ES
这是一个数值优化算法。它与遗传算法属于同一类(它们都是进化的),但CMA-ES与遗传算法截然不同。它是一个随机算法,没有导数,不需要计算目标函数的导数(不像梯度下降,它依赖于偏导数)。它的计算效率很高,被用于各种数值优化库,如Optuna。在这里我们只简要介绍一下CMA-ES,有关更详细的解释,请参阅最后链接部分的文献。
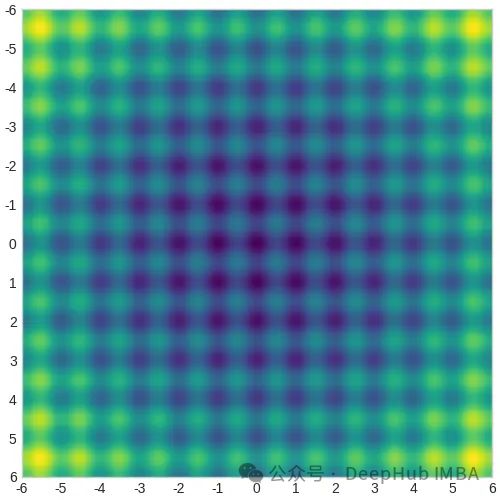
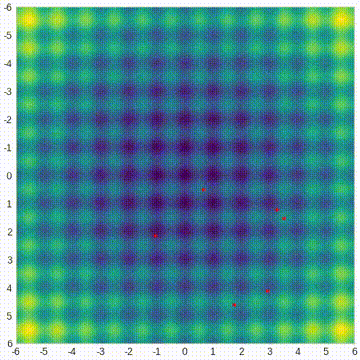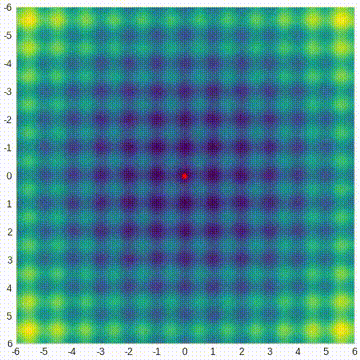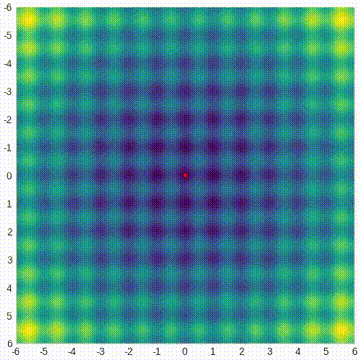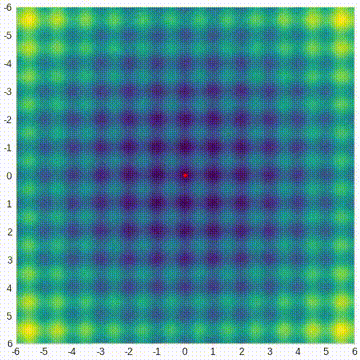
下面的热图显示了这个函数的值——颜色越亮意味着值越高。该函数在原点(0,0)处具有全局最小值,但它夹杂着许多局部极值。我们想通过CMA-ES找到全局最小值。
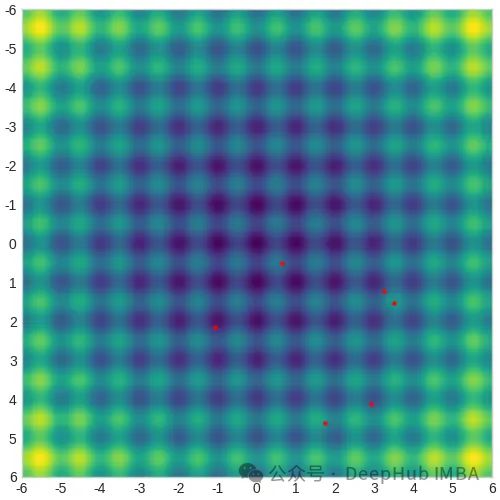
CMA-ES基于多元正态分布。它从这个分布中生成搜索空间中的测试点。但在开始之前,必须必须猜测分布的原始均值,以及它的标准差,但之后算法会迭代地修改所有这些参数,在搜索空间中扫描分布,寻找最佳的目标函数值。
Xi是算法在搜索空间中每一步产生的点的集合。Lambda是生成的点的个数。分布的平均值在每一步都会被更新,并且最终会收敛于真正的解。Sigma是分布的标准差——测试点的分布。C是协方差矩阵,它定义了分布的形状。根据C值的不同,分布可能呈“圆形”或更细长的椭圆形。对C的修改允许CMA-ES“潜入”搜索空间的某些区域,或避开其他区域。
上图中生成了6个点的种群,这是优化器为这个问题选择的默认种群大小。这是第一步。然后算法进行下面的步骤:
1、计算每个点的目标函数(Rastrigin)
2、更新均值、标准差和协方差矩阵,根据从目标函数中学到的信息,有效地创建一个新的多元正态分布
3、从新的分布中生成一组新的测试点
4、重复,直到满足某个准则(要么收敛于某个平均值,要么超过最大步数等)。
对于更新分布的均值是很简单的:计算每个测试点的目标函数后,给这些点分配权重,目标值越好的点权重越大,并从它们的位置计算加权和,这就成为新的均值。CMA-ES有效地将分布均值向目标值较好的点移动:
如果算法收敛于真解,那么分布的平均值也将收敛于该解。标准差会收敛于0。协方差矩阵将根据目标函数的位置改变分布的形状(圆形或椭圆形),扩展到有希望的区域,并避开不好的区域。
下面是一个显示了CMA-ES解决拉斯特里金问题时测试点的时间演变的GIF动画:
将CMA-ES用于特征选择
2D Rastrigin函数相对简单,因为它只有2个维度。但对于我们的特征选择问题,有N=213个维度。而且空间是不连续的。每个测试点是一个n维向量,其分量值为{0,1}。换句话说,每个测试点看起来像这样:[1,0,0,1,1,1,0,…]-一个二进制向量。
下面是使用cmaes库进行特征选择的CMA-ES代码的简单版本:
def cma_objective(fs):
features_use = ['const'] + [
f for i, f in enumerate(features_select) if fs[i,] == 1
]
lin_mod = sm.OLS(y_cmaes, X_cmaes[features_use], hasconst=True).fit()
return lin_mod.bic
X_cmaes = X.copy()
y_cmaes = y.copy()
features_select = [f for f in X_cmaes.columns if f != 'const']
dim = len(features_select)
bounds = np.tile([0, 1], (dim, 1))
steps = np.ones(dim)
optimizer = CMAwM(
mean=np.full(dim, 0.5),
sigma=1 / 6,
bounds=bounds,
steps=steps,
n_max_resampling=10 * dim,
seed=0,
)
max_gen = 100
best_objective_cmaes_small = np.inf
best_sol_raw_cmaes_small = None
for gen in tqdm(range(max_gen)):
solutions = []
for _ in range(optimizer.population_size):
x_for_eval, x_for_tell = optimizer.ask()
value = cma_objective(x_for_eval)
solutions.append((x_for_tell, value))
if value < best_objective_cmaes_small:
best_objective_cmaes_small = value
best_sol_raw_cmaes_small = x_for_eval
optimizer.tell(solutions)
best_features_cmaes_small = [
features_select[i]
for i, val in enumerate(best_sol_raw_cmaes_small.tolist())
if val == 1.0
]
print(f'best objective: {best_objective_cmaes_small}')
print(f'best features: {best_features_cmaes_small}')
CMA-ES优化器定义了对平均值和标准差的一些初始猜测。然后它循环许多代,创建测试点x_for_eval,用目标评估,修改分布(mean, sigma, covariance matrix)等等。每个x_for_eval点都是一个二进制向量[1,1,1,0,0,1,…]]用于从数据集中选择特征。
这里使用的是CMAwM()优化器(带边距的CMA)而不是默认的CMA()。默认的优化器可以很好地处理规则的、连续的问题,但是这里的搜索空间是高维的,并且只允许两个离散值(0和1)。默认优化器会卡在这个空间中。CMAwM()稍微扩大了搜索空间(虽然它返回的解仍然是二进制向量),可以以解除阻塞。
下图显示了CMA-ES代码寻找最佳解决方案的运行记录。热图显示了每一代每个特征的流行/流行程度(越亮=越受欢迎)。你可以看到有些特征总是很受欢迎,而另一些特征很快就过时了,还有一些特征后来才被“发现”。给定该问题的参数,优化器选择的总体大小为20个点(个体),因此特征受欢迎程度是在这20个点上平均的。
运行结果如下:
best objective: 33703.070530508514
best generation: 921
objective runs: 20000
time to best: 46.912 sec
它能够找到比SFS更好(更小)的目标值,它调用目标函数的次数更少(20k),并且花费了大约相同的时间。
在研究了传统的优化算法(遗传算法、模拟退火等)之后,CMA-ES是一个非常好的解决方案,它几乎没有超参数,计算量很轻,它只需要少量的个体(点)来探索搜索空间,但它的性能却很好。如果需要解决优化问题,用它来测试对比是非常有帮助的。
遗传算法
最后我们再看看常用的遗传算法
遗传算法受到生物进化和自然选择的启发。在自然界中,生物(粗略地说)是根据它们所处环境中促进生存和繁殖成功的基因(特征)而被选择的。
对于特征选择,有N个特征并试图找到n个长度的二进制向量[1,0,0,1,1,1,…],选择特征(1 =特征选择,0 =特征拒绝),以最小化成本/目标函数。
每个这样的向量可以被认为是一个“个体”。每个向量分量(值0或值1)成为一个“基因”。通过应用进化和选择,有可能进化出一个个体群体,使其接近于我们感兴趣的目标函数的最佳值。
以下是GA的简要介绍。首先生成一群个体(向量),每个向量的长度为n。向量分量值(基因)是从{0,1}中随机选择的。在下面的图表中,N=12,总体规模为8。
在群体创建后,通过目标函数评估每个个体。
保留客观价值最好的个体,抛弃客观价值最差的个体。这里有许多可能的策略,从单纯的排名(这与直觉相反,并不是很有效)到随机对比选择(从长远来看,这是非常有效的)。还记得“explore-exploit ”困境吗?使用GA,我们很容易陷入这个问题,所以随机对比会比排名好好很多。
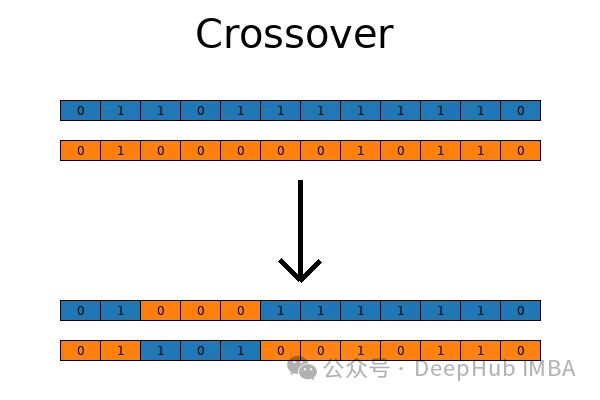
一旦最优秀的个体被选择出来,不太适合的个体被抛弃,就可以通过两种技术在基因库中引入变异了:交叉和突变。
交叉的工作原理与自然界完全一样,当两个生物交配并产生后代时:来自父母双方的遗传物质在后代中“混合”,具有一定程度的随机性。
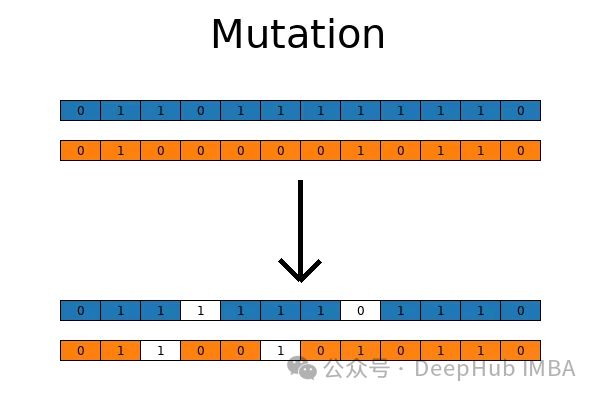
突变也是自然中发生的事情,当遗传物质发生随机突变时,新的价值被引入基因库,增加了它的多样性。
然后个体再次通过目标函数进行评估,选择发生,然后交叉,突变等等。
如果目标函数在某些代数内停止改进,则循环可能会被中断。或者可以为评估的总代数设置一个值,或者运行时间等等,在停止后具有最佳客观价值的个人应该被认为是问题的“解决方案”。
我们可以将GA封装在Optuna中,让Optuna自己寻找最佳的超参数——但这在计算上是非常非常耗时的。
将遗传算法用于特征选择
为了演示,我们使用了非常强大的deep库,如果你不熟悉这个库可能看起来有点困难,我们将尽量保持代码的简单。
# to maximize the objective
# fitness_weights = 1.0
# to minimize the objective
fitness_weights = -1.0
# copy the original dataframes into local copies, once
X_ga = X.copy()
y_ga = y.copy()
# 'const' (the first column) is not an actual feature, do not include it
X_features = X_ga.columns.to_list()[1:]
try:
del creator.FitnessMax
del creator.Individual
except Exception as e:
pass
creator.create("FitnessMax", base.Fitness, weights=(fitness_weights,))
creator.create(
"Individual", array.array, typecode='b', fitness=creator.FitnessMax
)
try:
del toolbox
except Exception as e:
pass
toolbox = base.Toolbox()
# Attribute generator
toolbox.register("attr_bool", random.randint, 0, 1)
# Structure initializers
toolbox.register(
"individual",
tools.initRepeat,
creator.Individual,
toolbox.attr_bool,
len(X_features),
)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
def evalOneMax(individual):
# objective function
# create True/False selector list for features
# and add True at the start for 'const'
cols_select = [True] + [i == 1 for i in list(individual)]
# fit model using the features selected from the individual
lin_mod = sm.OLS(y_ga, X_ga.loc[:, cols_select], hasconst=True).fit()
return (lin_mod.bic,)
toolbox.register("evaluate", evalOneMax)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
random.seed(0)
pop = toolbox.population(n=300)
hof = tools.HallOfFame(1)
pop, log = algorithms.eaSimple(
pop, toolbox, cxpb=0.5, mutpb=0.2, ngen=10, halloffame=hof, verbose=True
)
best_individual_ga_small = list(hof[0])
best_features_ga_small = [
X_features[i] for i, val in enumerate(best_individual_ga_small) if val == 1
]
best_objective_ga_small = (
sm.OLS(y_ga, X_ga[['const'] + best_features_ga_small], hasconst=True)
.fit()
.bic
)
print(f'best objective: {best_objective_ga_small}')
print(f'best features: {best_features_ga_small}')
代码创建了定义个体和整个种群的对象,以及用于评估(目标函数)、交叉、突变和选择的策略。它从300个个体的种群开始,然后调用eaSimple()(一个交叉、突变、选择的固定序列),我们这里只运行10代,其中绝对最好的个体被保留下来,以免在选择过程中意外突变或被跳过等。
这段简单的代码很容易理解,但效率不高,运行的结果如下:
best objective: 33705.569572544795
best generation: 787
objective runs: 600525
time to best: 157.604 sec
下面的热图显示了各代中每个特征的受欢迎程度(颜色越亮=越受欢迎)。可以看到有些特征总是很受欢迎,有些特征很快就被拒绝了,而另一些特征可能随着时间的推移变得更受欢迎或不那么受欢迎。
方法对比总结
我们尝试了三种不同的技术:SFS、CMA-ES和GA。
这些测试是在AMD Ryzen 7 5800X3D(8/16核)机器上进行的,运行Ubuntu 22.04和Python 3.11.7。SFS和GA是使用有16个线程来运行目标函数。CMA-ES是单进程的——在多线程中运行它似乎并没有提供显著的改进,这可能是算法没有支持多线程,下面是运行时间
SFS: 44.850 sec
GA: 157.604 sec
CMA-ES: 46.912 sec
目标函数调用的次数:
SFS: 22791
GA: 600525
CMA-ES: 20000
目标函数的最佳值-越少越好:
SFS: 33708.9860
GA: 33705.5696
CMA-ES: 33703.0705
CMA-ES找到了最佳目标函数。它的运行时间与SFS相当。它只调用目标函数20k次,是所有方法中调用次数最少的。别忘了,他还是单线程的
GA能够在目标函数上超过SFS,但它是最慢的。它调用目标函数的次数比其他方法多一个数量级。这是因为我们可以认为他是一个半随机的过程,因为遗传突变这个东西没有算法可解释。
SFS速度很快(可以在所有CPU内核上运行),但性能一般。但它是目前最简单的算法。
如果你只是想用一个简单的算法快速估计出最佳的特征集,那么SFS还不错。如果你想要绝对最好的客观价值,CMA-ES似乎是首选,并且它也不慢。
最后本文的代码:
https://avoid.overfit.cn/post/3bd329a18abe4ab4af36e6b7ceaef469
作者:Florin Andrei