5.逻辑回归 Logistic Regression
这章感觉也不难,但终究是感觉而已。所有的不难终归都是不熟练,自己只是看着好搞而已,等到自己亲自上手用这个知识敲一段时,说不定又磕磕绊绊了呢。
我觉得这章的知识可以用于我的毕业设计,即用某个算法替代论文中的某个算法,提高预测结果。
先mark一下。
————————————————————————分割线————————————————————————
逻辑回归的定义:
逻辑回归,是一种名为“回归”的线性分类器,其本质是由线性回归变化而来的,一种广泛使用于分类问题中的广义回归算法。
θ被统称为模型的参数。(θ是一组参数,具体数学背景和定理推导就略过了,记住就好了,只讲怎么用。)
我们使用”损失函数“这个评估指标,来衡量参数θ的优劣,即这一组参数能否使模型在训练集上表现优异:
损失函数小,模型在训练集上表现优异,拟合充分,参数优秀
损失函数大,模型在训练集上表现差劲,拟合不足,参数糟糕
我们追求能够让损失函数最小化的参数组合。
对逻辑回归中过拟合的控制,通过正则化来实现。
正则化及重要参数penalty和C:
正则化是用来防止模型过拟合的过程,常用的有L1正则化和L2正则化两种选项,分别通过在损失函数后加上参数向量θ的L1范式和L2范式的倍数来实现。这个增加的范式,被称为“正则项”,也被称为"惩罚项"(penalty)。
penalty:
可以输入"l1"或"l2"来指定使用哪一种正则化方式,不填写默认"l2"。
注意,若选择"l1"正则化,参数solver仅能够使用”liblinear",
若使用“l2”正则化,参数solver中 所有的求解方式都可以使用。
C:
正则化强度的倒数,必须是一个大于0的浮点数,不填写默认1.0,即默认一倍正则项。C越小,对损失函数的惩罚越重,正则化的效力越强,参数θ会逐渐被压缩得越来越小。
当正则化/惩罚度的强度逐渐增大(即C逐渐变小), 参数θ的取值会逐渐变小,
但L1正则化会将参数压缩为0,L2正则化只会让参数尽量小,不会取到0。
什么情况用L1和L2?
L1正则化本质是一个特征选择的过程,掌管了参数的“稀疏性”。L1正则化越强,参数向量中就越多的参数为0,参数就越稀疏,选出来的特征就越少,以此来防止过拟合。因此,如果 特征量很大,数据维度很高,我们会倾向于使用L1正则化。
L2正则化在加强的过程中,会尽量让每个特征对模型都有一些小的贡献,但携带信息少,对模型贡献不大的特征的参数会非常接近于0。
通常来说,如果我们的主要目的只是为了防止过拟合,选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合,模型在未知数据集上的效果表现很差,就可以考虑L1正则化。
以下为一个实例,建立两个逻辑回归,L1正则化和L2正则化的差别就一目了然了:
from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split # 要看逻辑回归在训练集上的表现如何,所以导入这个库
from sklearn.metrics import accuracy_score
data=load_breast_cancer()
x=data.data
y=data.target
lrl1=LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2=LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
lrl1=lrl1.fit(x,y)
# 逻辑回归的重要属性coef_(其实就是θ),查看每个特征所对应的参数θ
lrl1.coef_lrl2=lrl2.fit(x,y)
lrl2.coef_可以看见,当我们选择L1正则化的时候,许多特征的参数都被设置为了0,这些特征在真正建模的时候,就不会出现在我们的模型当中了,而L2正则化则是对所有的特征都给出了参数。
以下代码用来判断L1和L2哪个正则化的效果最好
知识点说明:
np.linspace(0.05, 1, 19) 从0.05到1,从小到大取出19个数字
LR()的参数:
penalty:可选择的值为"l1"和"l2".分别对应L1的正则化和L2的正则化,默认是L2的正则化。
solver:决定了我们对逻辑回归损失函数的优化方法,有4种算法可以选择:liblinear,lbfgs,newton-cg,sag
C:正则化强度的倒数,必须是一个大于0的浮点数,不填写默认1.0,即默认一倍正则项。C越小,对损失函数的惩罚越重,正则化的效力越强,参数θ会逐渐被压缩得越来越小。
max_iter:迭代次数
lrl1.predict(Xtrain):预测特征矩阵对应的逻辑回归的结果
Ytrain:真实的结果
accuracy_score(模型的预测值,数据的真实值) 输出两者的差异的精确度
——————————————————————————————————————————————————————————————————————————————————————————————————
代码:
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(x,y,test_size=0.3,random_state=420)
for i in np.linspace(0.05,1,19):
# 实例化模型
lrl1=LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
lrl2=LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
lrl1=lrl1.fit(Xtrain,Ytrain)
l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
lrl2 = lrl2.fit(Xtrain,Ytrain)
l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
# 画图
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):
plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4)
#图例的位置在哪里?4表示,右下角
plt.show()
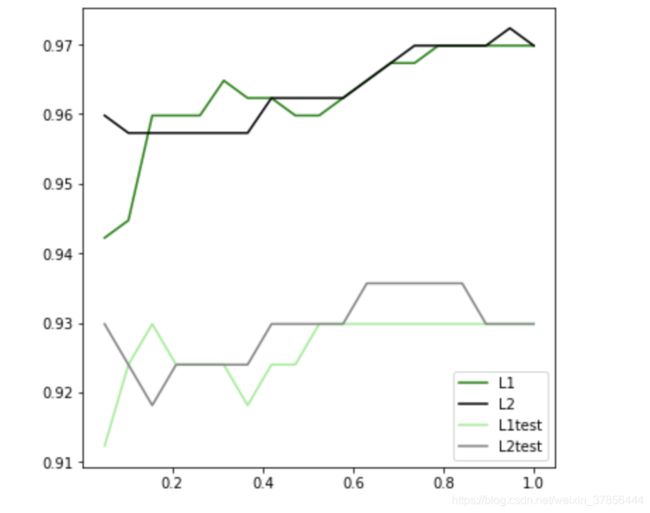
可见,至少在我们的乳腺癌数据集下,两种正则化的结果区别不大。
但随着C的逐渐变大,正则化的强度越来越小,模型在训练集和测试集上的表现都呈上升趋势,直到C=0.8左右,训练集上的表现依然在走高。
但模型在未知数据集上的表现开始下跌,这时候就是出现了过拟合。
我们可以认为,C设定为0.9会比较好。
在实际使用时,基本就默认使用l2正则化,如果感觉到模型的效果不好,那就换L1试试看。