【数据结构和算法】反转链表

其他系列文章导航

Java基础合集
数据结构与算法合集

设计模式合集

多线程合集

分布式合集

ES合集

---

文章目录

其他系列文章导航

文章目录

前言

一、题目描述

二、题解

2.1 方法一：迭代（双指针）

2.2 方法二：递归

三、代码

3.1 方法一：迭代（双指针）

3.2 方法二：递归

四、复杂度分析

4.1 方法一：迭代（双指针）

4.2 方法二：递归

---

前言

这是力扣的 206 题，难度为简单，解题方案有很多种，本文讲解我认为最奇妙的一种。

继续开始链表的模块了，这道题是一道非常好的队列的例题，很有代表性。

---

一、题目描述

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

---

二、题解

因为进阶要求两种方法来解决这道题目，所以本文都讲解！

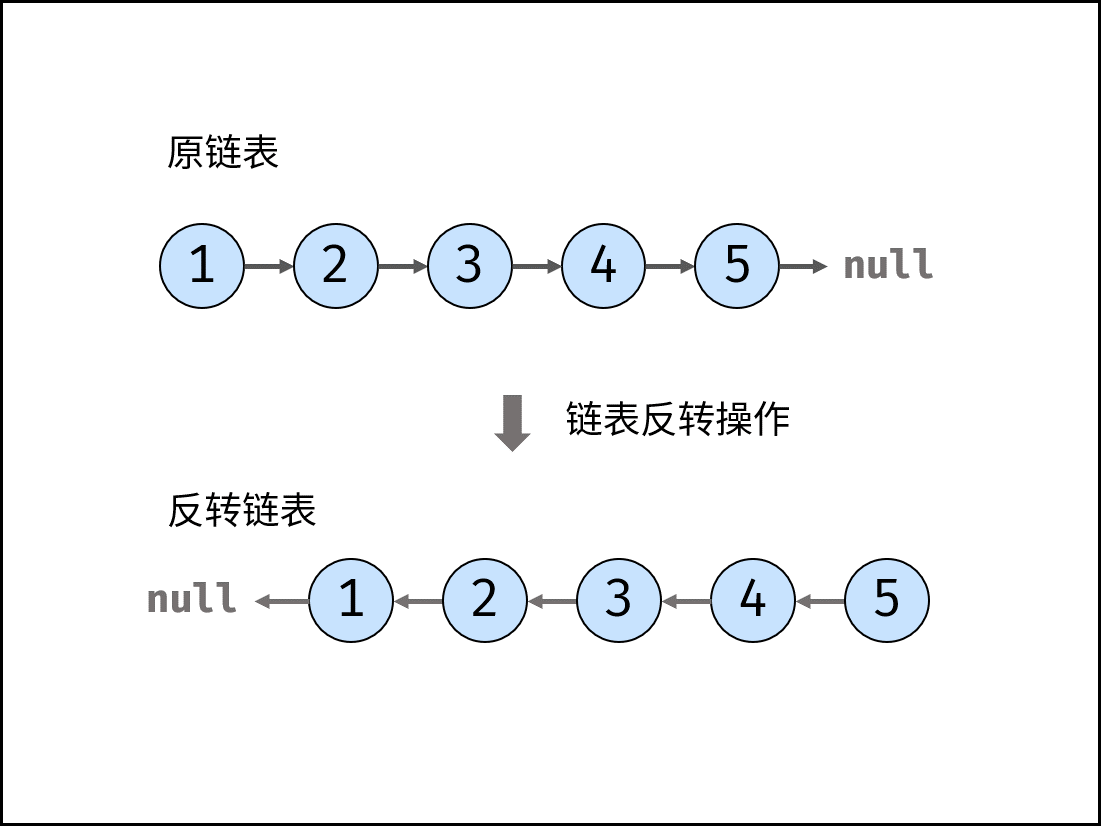
如下图所示，题目要求将链表反转。本文介绍迭代（双指针）、递归两种实现方法。

2.1 方法一：迭代（双指针）

思路与算法：

假设链表为 1→2→3→∅，我们想要把它改成 ∅←1←2←3。

在遍历链表时，将当前节点的 next 指针改为指向前一个节点。由于节点没有引用其前一个节点，因此必须事先存储其前一个节点。在更改引用之前，还需要存储后一个节点。最后返回新的头引用。

2.2 方法二：递归

递归版本稍微复杂一些，其关键在于反向工作。假设链表的其余部分已经被反转，现在应该如何反转它前面的部分？

假设链表为：
n1→…→nk−1→nk→nk+1→…→nm→∅

若从节点 nk+1到 nm已经被反转，而我们正处于 nk。

n1→…→nk−1→nk→nk+1←…←nm

我们希望 nk+1的下一个节点指向 nk。

所以，nk.next.next=nk

需要注意的是 n1的下一个节点必须指向 ∅。如果忽略了这一点，链表中可能会产生环。

---

三、代码

3.1 方法一：迭代（双指针）

Java版本：

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head, pre = null;
        while(cur != null) {
            ListNode tmp = cur.next; // 暂存后继节点 cur.next
            cur.next = pre;          // 修改 next 引用指向
            pre = cur;               // pre 暂存 cur
            cur = tmp;               // cur 访问下一节点
        }
        return pre;
    }
}

C++版本：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *cur = head, *pre = nullptr;
        while(cur != nullptr) {
            ListNode* tmp = cur->next; // 暂存后继节点 cur.next
            cur->next = pre;           // 修改 next 引用指向
            pre = cur;                 // pre 暂存 cur
            cur = tmp;                 // cur 访问下一节点
        }
        return pre;
    }
};

Python版本：

class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        cur, pre = head, None
        while cur:
            tmp = cur.next # 暂存后继节点 cur.next
            cur.next = pre # 修改 next 引用指向
            pre = cur      # pre 暂存 cur
            cur = tmp      # cur 访问下一节点
        return pre

3.2 方法二：递归

Java版本：

 public ListNode reverseList(ListNode head) {
        return recur(head, null);
    }

    private ListNode recur(ListNode cur, ListNode pre) {
        if (cur == null) return pre;
        ListNode res = recur(cur.next, cur);
        cur.next = pre;
        return res;
    }

C++版本：

class ListNode {
public: 
    int val;
    ListNode* next;
};

ListNode* reverseList(ListNode* head) {
    ListNode* pre = nullptr;
    ListNode* cur = head;
    while (cur) {
        ListNode* next = cur->next;
        cur->next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}

Python版本：

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def reverseList(head):
    def recur(cur, pre):
        if not cur:
            return pre
        res = recur(cur.next, cur)
        cur.next = pre
        return res

    return recur(head, None)

---

四、复杂度分析

4.1 方法一：迭代（双指针）

• 时间复杂度 O(N) ： 遍历链表使用线性大小时间。
• 空间复杂度 O(1) ： 变量 pre 和 cur 使用常数大小额外空间。

4.2 方法二：递归

• 时间复杂度 O(N) ： 遍历链表使用线性大小时间。
• 空间复杂度 O(N) ： 遍历链表的递归深度达到 N ，系统使用 O(N) 大小额外空间。

---