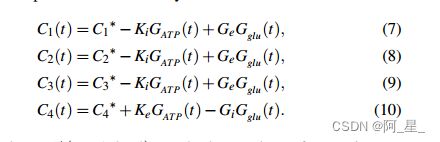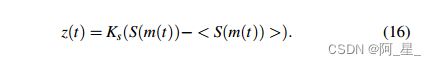学习日记4-星形胶质细胞释放的胶质递质在阿尔茨海默症中的重要作用：从动力学建模的角度

The important role of glial transmitters released by astrocytes in Alzheimer’s disease a perspective from dynamical modelling（星形胶质细胞释放的胶质递质在阿尔茨海默症中的重要作用：从动力学建模的角度）

未完待续~（学不动了，先更这些）

        本文旨在建立神经元群与星形胶质细胞的耦合模型，并在此基础上从动力学建模的角度探讨阿尔茨海默病(AD)脑电图(EEG)减慢的可能机制。

1. 星形胶质细胞

        胶质细胞可通过细胞突起连接血管和神经元，组成血脑屏障的一部分，此外还可以去除微环境中过多的钾离子、回收神经递质、调控血流方向、同步轴突的信号传导以及调节脑部能量代谢和稳态等。目前，研究人员发现星形胶质细胞功能障碍与许多神经退行性疾病有关，例如肌萎缩性脊髓侧索硬化症，亨廷顿综合征，帕金森病等。

Ⅱ. Methods

A. The proposed neuronal population-astrocyte population (NA) coupling network model（神经元群-星形胶质细胞群(NA)耦合网络模型）

        该模型是基于JR神经质量模型的改进，包含三个种群：锥体神经元种群(PY)，兴奋性中间神经元种群(EI)和抑制性中间神经元种群(II)。

        PY对EI和II都有兴奋性的投射。EI和II对PY分别有兴奋性和抑制性的投射。

神经元群-星形胶质细胞群(NA)耦合网络模型示意图

        图中C表示不同神经元群体之间突触接触的平均次数，Ks表示三个神经元群体对星形胶质细胞的相应反馈系数。红色箭头表示星形胶质细胞神经递质对兴奋性突触连接的影响，包含谷氨酸的兴奋作用和ATP的抑制作用；红色圆头表示星形胶质细胞神经递质对抑制性突触连接的影响。而绿色箭头则表示三个神经元群对星形胶质细胞的反馈。

        神经元群动力学方程：

y1y2y3分别代表投射到PY的兴奋性和抑制性作用，y3y4y5是他们的导数。y = y1−y2为感兴趣的模型输出，表示EEG放电活动。A、B、te、ti、p分别为兴奋性突触平均增益、抑制性突触平均增益、兴奋性时间常数、抑制性时间常数和兴奋性外部输入。S是将平均突触后膜电位转化为平均放电速率的S型函数e0, X0和r分别为种群最大发射率的一半，50%发射率时的电位值和X0处的s型函数斜率。

考虑到星形胶质递质对突触连接的影响，将Ci改为依赖星形胶质细胞的Ci(t)

C *为突触连接的基值。Ki和Ke分别是ATP对抑制性和兴奋性突触连接的影响系数。Gi和Ge分别代表谷氨酸对抑制性和兴奋性突触连接的影响系数。gllu (t)和GAT P(t)分别表示胶质谷氨酸和ATP的产生。

Cacyt和CaER分别是星形细胞细胞质和内质网中的钙浓度。

z(t)有助于星形胶质细胞与神经元群之间的相互作用，显示神经元群的突触活动并产生星形胶质细胞的输入信号。

S(m(t))表示PY、EI和II的平均发射速率，< S(m(t)) >由实际射速估算的，将时间常数w设置为0.5。至此，PY-EI-II-AS耦合网络的动力学由式(1)-(17)建模。

模型参数的简要说明及基线值

B.Data analysis and simulation methods（数据分析和仿真实验）

采用标准的四阶龙格-库塔积分法求解NA耦合网络模型的微分方程，时间分辨率固定为4ms。时序图的暂态时间会影响相对功率。

下面是四阶龙格-库塔积分法

本文所有的分析都是基于稳定时间序列，也就是说，所有的分析都不包括初始瞬态数据。模型输出采用下截止频率为1 Hz、上截止频率为50 Hz的带通滤波器进行滤波。功率谱密度的定量分析包括主导频率和特定频段的相对功率。

最大峰值频率被定义为振荡的主导频率。一个频段(8 ~ 13hz)或d + q频段(1 ~ 8hz)的相对功率是通过对相应频段内的相对功率谱密度求平均值来计算的。动态分岔图是使用延续包XPPAUTO完成的。

Ⅲ Resuls

1. 兴奋性和抑制性时间常数诱导AD的动力学机制

在本节中，我们改变兴奋和抑制时间常数来研究它们对AD的影响。

相对密度

 y1、y2分别代表投射到PY的兴奋性和抑制性作用，y1-y2表示模型shu'c'zhi

Ti表示抑制性时间常数；Te表示固定兴奋性时间常数；α频段(α波段，红线)、δ+θ频段(δ+θ波段，蓝线)和神经活动主导频率(DF，黄线)的相对功率演变。

改变抑制性时间常数ti，固定兴奋性时间常数te=10，可诱发AD的脑电图减慢现象。当ti在(21,37)范围内增大时，α波段的相对功率和DF减小，而δ+θ波段的相对功率增大。

如图2(a)所示，当ti 2(19;21)时，a波段的相对功率基本稳定在25.5左右，d + q波段的相对功率基本稳定在0.08左右。也就是说，神经振荡的力量主要集中在a波段，这与10.74左右的神经振荡的主导频率(DF)相吻合。

总的来说，随着ti从19增加到37，神经振荡的a波段功率减小，δ+θ波段功率增大。当ti > 37或ti < 19时，系统不呈现振荡节律状态。该结果与传统的实验脑电图测量结果一致，显示AD49-51患者的a波段活性降低，d +q波段活性增加。

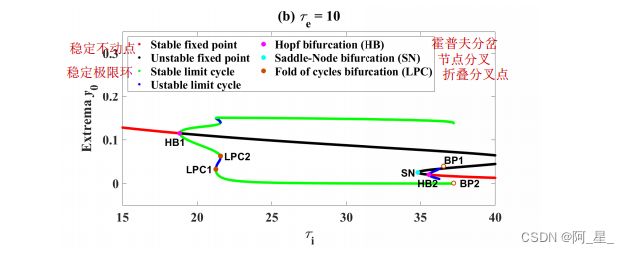
在ti 2(18:8287;37:2232)时，系统处于稳定极限环状态，即图2(a)所示的振荡节律状态。否则，系统将处于稳定平衡点状态，对应于图2(a)中的非振荡状态。也就是说，系统在超临界HB1(18.8287, 0.1151)之后和BP2(37.2232, 0.0011)之前都可能处于振荡状态。对于标记为BP的分叉点极限环，XPPAUTO不自动跟踪和计算分叉点。

当LPC1(21.2498,0.0400)出现而LPC2(21.5633, 0.0630)不出现即ti 2(21:24 . 98;21:56 . 33)时，系统处于两种节律振荡共存的稳定状态。在此参数区间内，与图2(a)相比，a频段的相对功率急剧下降，d频段的相对功率急剧上升。提示阿尔茨海默病脑电图减慢的动态性是LPC引起的振荡模式改变。在ti = 34:8286时，出现了一个鞍节点分岔(即SN)，但它显然不会改变系统的稳定解。当ti增加到35.5726时，出现亚临界HB2(35.5726, 0.0204)，系统呈现由稳定平衡点和稳定极限环组成的双稳态。

(c1-c6) y1−y2的时间序列和相对功率谱密度。

同样，兴奋时间常数te对神经振荡行为的影响如图3所示。我们还观察到与AD相关的脑电图节律的变化，包括a波段的相对功率降低，d +q波段的相对功率增加，振荡的主导频率降低(如图3(a)所示)。图3(c1-c6)给出了图3(a)中典型参数对应的时间序列和相对功率谱密度。我们可以看到，神经活动都是谐波振荡，但频率和振幅不同。有趣的是，图3(b)和图3(d)的分岔图显示，尽管神经振荡的DF和不同频段的相对功率有变化趋势，但动力系统在(10,33)范围内没有分岔。也就是说，在此参数设置下，te诱发的脑电图慢化现象的动态性更多是由于振荡幅度的变化，而不是频率的变化，这与ti不同。