机器学习练习 6 - Support Vector Machines(支持向量机)
机器学习练习 6 - Support Vector Machines(支持向量机)
Introduction
在本实验中,将使用支持向量机(SVMs)来构建垃圾邮件分类器。
1 Support Vector Machines(支持向量机)
在本实验的前半部分,将使用包含各种 2 D 2D 2D数据集的支持向量机(SVMs)。对这些数据集进行实验可以更加直观地了解SVMs的工作原理,以及如何在SVMs上使用高斯核。在本实验的后半部分,将使用SVMs来构建垃圾邮件分类器。
1.1 Example Dataset 1
从一个可以由线性边界分隔的二维数据集开始。在这个数据集中,正例子(用+表示)和负例子(用o表示)的位置表明可以由线性边界分割。但是,注意,在最左边有一个异常的正例子+,大约是 ( 0.1 , 4.1 ) (0.1,4.1) (0.1,4.1)。在本实验中,将看到这种特殊的例子如何影响SVM的决策边界。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.io import loadmat
from sklearn import svm
import seaborn as sns
def load_mat(path):
data=loadmat(path)
X=data['X']
y=data['y']
return X,y
path="./data/ex6data1.mat"
X,y=load_mat(path)
def plot_data(X,y,fig,ax):
data=pd.DataFrame(X,columns=['X1','X2'])
data['y']=y
positive=data[data['y'].isin([1])]
negative=data[data['y'].isin([0])]
ax.scatter(positive['X1'],positive['X2'],s=30,marker='+',c='black',label='Positive')
ax.scatter(negative['X1'],negative['X2'],s=30,marker='o',c='orange',label='Negative')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.legend()
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X, y,fig,ax)
plt.title("Example Dataset 1")
plt.show()
在本部分的实验中,将尝试对SVMs使用不同的C参数值。C参数是一个正数,它控制了对错误分类的训练数据的惩罚,其中C较大,说明SVM尝试正确地分类所有的数据,C类似于 1 λ \frac{1}{\lambda} λ1, λ \lambda λ是之前用于逻辑回归的正则化参数。
大多数SVM库会自动添加额外的特征,比如: x 0 , θ 0 x_0,\theta_0 x0,θ0,所以无需手动添加。
svc = svm.SVC(C=1, kernel='linear')
svc
SVC(C=1, kernel='linear')
svc.fit(X,y.flatten())
svc.score(X,y.flatten())
0.9803921568627451
可视化分类边界
def plot_boundary(svc,X,y,C,diff=10**-3):
x1,x2=decision_boundary(svc,X,diff)
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X, y,fig,ax)
ax.scatter(x1,x2,s=5,c='blue',label='Boundary')
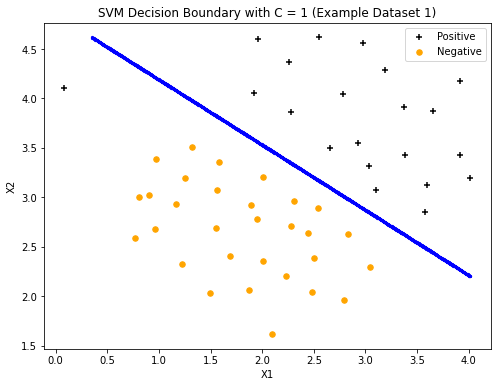
plt.title("SVM Decision Boundary with C = {} (Example Dataset 1)".format(C))
plt.show()
def decision_boundary(svc,X,diff=10**-3):
x1_min,x1_max=X[:,0].min(),X[:,0].max()
x2_min,x2_max=X[:,1].min(),X[:,1].max()
x1=np.linspace(x1_min,x1_max,2000)
x2=np.linspace(x2_min,x2_max,2000)#将整个平面分割为2000*2000的小方格,如果后面感觉运行太久可以适当缩小到500
cordinates = [(x, y) for x in x1 for y in x2]
x1, x2 = zip(*cordinates)
c_val=pd.DataFrame({'x1':x1,'x2':x2})
c_val['cval']=svc.decision_function(c_val[['x1','x2']])#对所有的小方格的:预测样本的置信度得分(接近0的就是分割边界)
decision=c_val[np.abs(c_val['cval'])<diff]
return decision.x1,decision.x2
当C=1时,发现SVM将决策边界放在两个数据集之间的间隙中,并将最左边的数据点错误分类。
plot_boundary(svc,X,y,1,10**-3)
svc2 = svm.SVC(C=100,kernel='linear')
svc2
SVC(C=100, kernel='linear')
svc2.fit(X,y.flatten())
svc2.score(X,y.flatten())
1.0
当C=100时,发现SVM对每个数据都正确分类,但是该决策边界与数据匹配并不自然。
plot_boundary(svc2,X,y,100,10**-3)
综上:
- 当
C比较小时模型对错误分类的惩罚较小,比较宽松,允许一定的错误分类存在,间隔较大。 - 当
C比较大时模型对错误分类的惩罚较大,比较严格,错误分类少,间隔较小。
1.2 SVM with Gaussian Kernels
在这节实验,将使用SVMs来进行非线性分类并且在非线性可分的数据集上使用高斯核SVMs。
1.2.1 Gaussian Kernel(高斯核)
为了用SVM找到非线性决策边界,需要实现一个高斯核。可以把高斯核看作一个相似度函数,用来度量一对数据 ( x ( i ) , x ( j ) ) (x^{(i)},x^{(j)}) (x(i),x(j))之间的"距离"。高斯核有一个参数 σ \sigma σ,决定了相似性下降至 0 0 0的速度。
高斯核定义如下:
这里使用sklearn自带的svm中的核函数即可:
def GaussKernel(x1,x2,sigma):
return np.exp(-np.sum((x1-x2)**2)/(2*sigma**2))
使用示例数据 x 1 = [ 1 , 2 , 1 ] , x 2 = [ 0 , 4 − 1 ] , σ = 2 x_1=[1,2,1],x_2=[0,4-1],\sigma=2 x1=[1,2,1],x2=[0,4−1],σ=2运行的结果约为 0.324652 0.324652 0.324652。
x1,x2,sigma=np.array([1,2,1]),np.array([0,4,-1]),2
GaussKernel(x1, x2, sigma)
0.32465246735834974
1.2.2 Example Dataset 2
接下来的实验中的数据的分布图如下图所示,可以观察到,该数据集的正例子和负例子之间没有线性决策边界。不过,通过使用高斯核SVM,将能够学习到一个非线性决策边界,它在该数据集表现得相当好。
path="./data/ex6data2.mat"
X2,y2=load_mat(path)
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X2,y2,fig,ax)
plt.title("Example Dataset 2")
plt.show()
上面已经正确地实现了高斯核函数GaussKernel,接下来将继续在这个数据集上用高斯核训练SVM。下图绘制了具有高斯核的SVM所找到的决策边界,该决策边界能够正确地分离大多数正负例子,并且很自然地遵循了数据集的轮廓。
sigma=0.1
gamma=np.power(sigma,-2)/2
clf=svm.SVC(C=1,kernel='rbf',gamma=gamma)
model=clf.fit(X2, y2.flatten())
clf.score(X2, y2.flatten())
0.9895712630359212
dx1,dx2=decision_boundary(model,X2,diff=0.01) #找到决策边界的点
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X2, y2, fig, ax)
ax.scatter(dx1,dx2,s=5)
plt.title("SVM (Gaussian Kernel) Decision Boundary (Example Dataset 2)")
plt.show()
1.2.3 Example Dataset 3
在这部分实验中,将进了解关于如何使用具有高斯核的SVM。首先绘制样例数据集 3 3 3中的数据分布图:
def load_mat3(path):
data=loadmat(path)
X=data['X']
y=data['y']
Xval=data['Xval']
yval=data['yval']
return X,y,Xval,yval
path="./data/ex6data3.mat"
X3,y3,X3val,y3val=load_mat3(path)
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X3,y3,fig,ax)
plt.title("Example Dataset 3")
plt.show()
第 3 3 3个数据集给出了训练集和验证集,并且基于验证集的性能来为SVM模型找到最优超参数。对于 C , σ C,\sigma C,σ,有候选值 ( 0.01 , 0.03 , 0.1 , 0.3 , 1 , 3 , 10 , 30 ) (0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30) (0.01,0.03,0.1,0.3,1,3,10,30)。尝试上面列出的 C C C和 σ \sigma σ的 8 8 8个值中的每个,最终将训练和评估(在交叉验证集上)共 64 64 64个不同的模型。
C_values=[0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
sigma_values=[0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30]
best_score=0
best_params={'C':None,'sigma':None}
for C in C_values:
for sigma in sigma_values:
clf=svm.SVC(C=C,kernel='rbf',gamma=sigma)
model=clf.fit(X3, y3.flatten())
score=clf.score(X3val, y3val.flatten())
if score>best_score:
best_score=score
best_params['C'],best_params['sigma']=C,sigma
best_score,best_params
(0.965, {'C': 3, 'sigma': 30})
clf=svm.SVC(C=best_params['C'],kernel='rbf',gamma=best_params['sigma'])
model=clf.fit(X3, y3.flatten())
clf.score(X3val, y3val.flatten())
0.965
根据上面的代码找到了最佳参数C和sigma,SVM得到了下图的决策边界。
dx1,dx2=decision_boundary(model,X3,diff=0.005) #找到决策边界的点
fig,ax=plt.subplots(figsize=(8,6))
plot_data(X3, y3, fig, ax)
ax.scatter(dx1,dx2,s=5)
plt.title("SVM (Gaussian Kernel) Decision Boundary (Example Dataset 3)")
plt.show()
2 Spam Classification(垃圾邮件分类)
在本部分的实验中,将使用SVMs来构建垃圾邮件过滤器。
接下来将训练一个分类器来分类给定的电子邮件(x)是垃圾邮件(y=1)还是非垃圾邮件(y=0),需要将每个电子邮件转换为一个特征向量 x ∈ R n x \in R^n x∈Rn
2.1 Preprocessing Emails(预处理电子邮件)
在开始执行机器学习任务之前,查看电子邮件的类型,下图显示了一个包含一个URL、电子邮件地址(在末尾)、数字和美元金额的电子邮件。虽然许多电子邮件包含类似实体(例如,数字、URL、电子邮件地址),但特定的实体(例如,特定的URL或特定的金额)在几乎每封电子邮件中都是不同的。因此,在处理电子邮件时经常使用的一种方法是"规范化"这些值,这样所有的url都处理成相同的,所有数字都处理成相同的。例如,用字符串httpaddr替换电子邮件中的URL,表示存在一个URL。这样做可以让垃圾邮件分类器根据是否存在URL来做出分类决定。这可以提高垃圾邮件分类器的性能,因为垃圾邮件发送者通常会将URL随机化,因此在新的垃圾邮件片段中再次看到特定出现过的URL的几率非常小。
with open("./data/emailSample1.txt","r") as f:
email=f.read()
print(email)
> Anyone knows how much it costs to host a web portal ?
>
Well, it depends on how many visitors you're expecting.
This can be anywhere from less than 10 bucks a month to a couple of $100.
You should checkout http://www.rackspace.com/ or perhaps Amazon EC2
if youre running something big..
To unsubscribe yourself from this mailing list, send an email to:
[email protected]
所以接下来,需要对读取到的邮件作如下处理:
- Lower-casing: 把整封邮件转化为小写
- Stripping HTML: 移除所有
HTML标签,只保留内容 - Normalizing URLs: 将所有的
URL替换为字符串httpaddr - Normalizing Email Addresses: 所有的地址替换为
emailaddr - Normalizing Dollars: 所有dollar符号(
$)替换为dollar - Normalizing Numbers: 所有数字替换为
number - Word Stemming(词干提取): 将所有单词还原为词源。例如
discount,discounts,discountedanddiscounting都替换为discount - Removal of non-words: 移除所有非文字类型,所有的空格(
tabs,newlines,spaces)调整为一个空格
将上面的邮件进行上述的预处理,结果如下图所示。虽然预处理留下了单词片段和非单词,但这种形式对于执行特征提取更容易处理。
import re
def processEmail(email):
email=email.lower()
email=re.sub('<[^<>]>',' ',email)
email=re.sub('(http|https)://[^\s]*','httpaddr',email)
email=re.sub('[^\s]+@[^\s]+','emailaddr',email)
email=re.sub('[\$]+','dollar',email)
email=re.sub('[\d]+','number',email)
return email
processEmail(email)
"> anyone knows how much it costs to host a web portal ?\n>\nwell, it depends on how many visitors you're expecting.\nthis can be anywhere from less than number bucks a month to a couple of dollarnumber. \nyou should checkout httpaddr or perhaps amazon ecnumber \nif youre running something big..\n\nto unsubscribe yourself from this mailing list, send an email to:\nemailaddr\n\n"
接下来提取词干并且去除非字符内容。
import nltk, nltk.stem.porter # 英文分词算法
def email_TokenList(email):
stemmer=nltk.stem.porter.PorterStemmer()
email=processEmail(email)
tokens=re.split('[ \@\$\/\#\.\-\:\&\*\+\=\[\]\?\!\(\)\{\}\,\'\"\>\_\<\;\%]',email)
tokenList=[]
for token in tokens:
token=re.sub('[^a-zA-Z0-9]','',token)
stemmed = stemmer.stem(token)#提取词根
if(len(token)):
tokenList.append(stemmed)
return tokenList
在对电子邮件进行预处理后,得到电子邮件的单词列表(如下)。接下来选择在分类器中使用哪些词,以及需要忽略哪些词。
email_TokenList(email)
['anyon',
'know',
'how',
'much',
'it',
'cost',
'to',
'host',
'a',
'web',
'portal',
'well',
'it',
'depend',
'on',
'how',
'mani',
'visitor',
'you',
're',
'expect',
'thi',
'can',
'be',
'anywher',
'from',
'less',
'than',
'number',
'buck',
'a',
'month',
'to',
'a',
'coupl',
'of',
'dollarnumb',
'you',
'should',
'checkout',
'httpaddr',
'or',
'perhap',
'amazon',
'ecnumb',
'if',
'your',
'run',
'someth',
'big',
'to',
'unsubscrib',
'yourself',
'from',
'thi',
'mail',
'list',
'send',
'an',
'email',
'to',
'emailaddr']
2.1.1 Vocabulary List
在本节实验中,只选择最经常出现的单词作为单词集(词汇表)。由于在训练集中很少出现的单词一般也只出现在少数电子邮件中,它们可能会导致模型过拟合。词汇表vocab.txt里面存储了在实际中经常使用的单词,共 1899 1899 1899个。(在实践中,词汇表大约有1万到5万字)。在词汇表中,将预处理电子邮件中的每个单词映射到一个单词索引列表中,其中包含词汇和单词索引。
完成processEmail函数,传入字符串str(处理过的电子邮件中的单个单词),然后在词汇表中查找该单词,看它是否存在于词汇表列表中,如果存在,将单词的索引添加到单词索引变量中;如果不存在,可以跳过这个词。
def processEmail_index(email,vocab):
token=email_TokenList(email)
index=[i for i in range(len(vocab)) if vocab[i] in token]
return index
vocab = pd.read_table('./data/vocab.txt',names=['words'])
vocab=vocab.values
processEmail_index(email, vocab)
[70,
85,
88,
161,
180,
237,
369,
374,
430,
478,
529,
530,
591,
687,
789,
793,
798,
809,
882,
915,
944,
960,
991,
1001,
1061,
1076,
1119,
1161,
1170,
1181,
1236,
1363,
1439,
1476,
1509,
1546,
1662,
1675,
1698,
1757,
1821,
1830,
1892,
1894,
1895]
2.2 Extracting Features from Emails(从电子邮件中提取特征)
接下来实现功能提取,将每个电子邮件转换为一个 R n R^n Rn的向量。电子邮件的特性 x i ∈ { 0 , 1 } x_i\in \lbrace0,1\rbrace xi∈{0,1}表示第 i i i个单词是否出现在电子邮件中,如果第 i i i个单词在电子邮件中,那么 x i = 1 x_i=1 xi=1;否则 x i = 0 x_i=0 xi=0。因此,一个电子邮件中的特征将看起来就像:
编写函数emailFeatures完成上述的功能,运行代码,可以看到特征向量的长度为 1899 1899 1899并且有 45 45 45个非零项。
def emailFeatures(email):
df = pd.read_table('./data/vocab.txt',names=['words'])
vocab=df.values
vector=np.zeros(len(vocab))
vocal_index=processEmail_index(email,vocab)
for i in vocal_index:
vector[i]=1
return vector
vector=emailFeatures(email)
print('vector had length {} and {} non-zero entries'.format(len(vector), int(vector.sum())))
vector had length 1899 and 45 non-zero entries
2.3 Training SVM for Spam Classification(垃圾邮件分类-SVM)
spamTrain.mat包含 4000 4000 4000个垃圾邮件和非垃圾邮件的训练数据,spamTest.mat包含 1000 1000 1000个测试数据。每个原始电子邮件使用processEmail函数和emailFeatures函数处理,并转换为一个向量 x ( i ) ∈ R 1899 x^{(i)}\in R^{1899} x(i)∈R1899。
加载数据集之后,训练SVM进行分类:垃圾邮件 y = 1 y=1 y=1和非垃圾邮件(y=0)。训练完成,分类器得到的训练准确率约为 99.8 % 99.8\% 99.8%,测试准确率约为 98.5 % 98.5\% 98.5%。
path="./data/spamTrain.mat"
X,y=load_mat(path)
path="./data/spamTest.mat"
data=loadmat(path)
Xtest,ytest=data["Xtest"],data["ytest"]
X.shape,y.shape,Xtest.shape,ytest.shape
((4000, 1899), (4000, 1), (1000, 1899), (1000, 1))
每个文档已经转换为一个向量,其中 1899 1899 1899对应于词汇表中的 1899 1899 1899个单词。 它们的值为二进制,表示文档中是否存在单词。
clf=svm.SVC(C=0.1,kernel='linear')
clf.fit(X,y)
clf.score(X,y)
D:\Python\lib\site-packages\sklearn\utils\validation.py:63: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
return f(*args, **kwargs)
0.99825
clf.score(Xtest,ytest)
0.989
2.4 Top Predictors for Spam
为了更好地理解垃圾邮件分类器是如何工作的,可以检查参数,看看分类器认为哪些词最能预测到垃圾邮件。接下来在分类器中找到最大的参数(正数),并显示相应的单词。因此,如果电子邮件包含"保证"、“删除”、"美元"和"价格"等词,它很可能被归类为垃圾邮件。
kw=np.eye(1899)
spam_val=pd.DataFrame({'index':range(1899)})
spam_val['is_spam']=clf.decision_function(kw)
spam_val['is_spam'].describe()
count 1899.000000
mean 0.184175
std 0.086875
min -0.418804
25% 0.141325
50% 0.185384
75% 0.225760
max 0.686941
Name: is_spam, dtype: float64
decision=spam_val[spam_val['is_spam']>0.4]
decision
| index | is_spam | |
|---|---|---|
| 49 | 49 | 0.423638 |
| 155 | 155 | 0.531392 |
| 173 | 173 | 0.415344 |
| 297 | 297 | 0.652244 |
| 390 | 390 | 0.419589 |
| 476 | 476 | 0.509960 |
| 478 | 478 | 0.415967 |
| 554 | 554 | 0.413357 |
| 698 | 698 | 0.434625 |
| 738 | 738 | 0.569949 |
| 791 | 791 | 0.432732 |
| 965 | 965 | 0.439794 |
| 1066 | 1066 | 0.443626 |
| 1088 | 1088 | 0.440269 |
| 1123 | 1123 | 0.401540 |
| 1190 | 1190 | 0.686941 |
| 1263 | 1263 | 0.447497 |
| 1298 | 1298 | 0.453625 |
| 1373 | 1373 | 0.411073 |
| 1397 | 1397 | 0.609197 |
| 1460 | 1460 | 0.419283 |
| 1795 | 1795 | 0.554038 |
| 1808 | 1808 | 0.418275 |
| 1851 | 1851 | 0.456052 |
vocab = pd.read_csv('./data/vocab.txt',names=['index','words'],sep='\t')
vocab.head()
| index | words | |
|---|---|---|
| 0 | 1 | aa |
| 1 | 2 | ab |
| 2 | 3 | abil |
| 3 | 4 | abl |
| 4 | 5 | about |
spam_voc=vocab.loc[list(decision['index'])]
spam_voc
| index | words | |
|---|---|---|
| 49 | 50 | al |
| 155 | 156 | basenumb |
| 173 | 174 | below |
| 297 | 298 | click |
| 390 | 391 | da |
| 476 | 477 | dollar |
| 478 | 479 | dollarnumb |
| 554 | 555 | enumb |
| 698 | 699 | ga |
| 738 | 739 | guarante |
| 791 | 792 | hour |
| 965 | 966 | lo |
| 1066 | 1067 | most |
| 1088 | 1089 | nbsp |
| 1123 | 1124 | numberb |
| 1190 | 1191 | our |
| 1263 | 1264 | pleas |
| 1298 | 1299 | price |
| 1373 | 1374 | recent |
| 1397 | 1398 | remov |
| 1460 | 1461 | se |
| 1795 | 1796 | visit |
| 1808 | 1809 | want |
| 1851 | 1852 | will |