力扣刷题框架——二叉树的搜索和回溯
二叉树的搜索和回溯
- 1. BFS
-
- 1.1 基本框架
- 1.2 例题
-
- 1.2.1 剑指offer 13. 机器人的运动范围
- 2. DFS
-
- 2.1 基本框架
- 2.2 例题
-
- 2.2.1 剑指offer 26. 树的子结构
- 2.2.2 矩阵中的路径
- 2.2.3 剑指 Offer 34. 二叉树中和为某一值的路径
都是剑指offer里面的题,关于二叉树的搜索和回溯算法还挺普遍的哈,之前总结过链接在下面:
- DFS+回溯剪枝
- BFS
所以这次算是温故而知新。
1. BFS
一般涉及到层序遍历(树、矩阵的横向搜索)可以考虑用BFS。
1.1 基本框架
public void bfs(TreeNode root){
if(root==null)//其他终止条件
return;
Queue<T> queue = new LinkedList<>();
Set<T> visited;//看情况,设置这个是为了避免走回头路
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
//由当前节点向四周扩散
for(int i=0;i<size;i++){
TreeNode cur = queue.poll();
if(cur is target){//如果当前节点满足要求
//加入到结果集合中
}
if(cur.left!=null){
queue.offer(cur.left);
visited.add(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
visited.add(cur.right);
}
}
}
}
1.2 例题
剑指offer32-I、II、III直接套框架可A。
1.2.1 剑指offer 13. 机器人的运动范围
题目描述
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
输入
m = 2, n = 3, k = 1
输出
3
结题思路
直接想法就是遍历所有格子,计算机器人所能到的格子数。这里机器人有两种运动方式:一个是向下走到底再回退——这就涉及到DFS+回溯/剪枝;另一个是以平推的方式进行,每向下走一格就横向搜索一次——BFS。这里先介绍BFS。
算法
- 初始化:初始化队列并加入(0,0),再初始化一个标记集合visited保存走过的格子。
- 循环遍历:遍历整个队列直至为空,如果所在坐标超过边界或者数位之和大于k那么这个格子不能用,否则就计入结果总数(格子可用);
- 更新队列和visited集合:把这个格子左边和下方的格子加入队列,该格子对应的坐标设为true。表示已经访问过了。
代码
public int movingCount(int m, int n, int k) {
//bfs
return bfs(m,n,k);
}
public int bfs(int m,int n,int k){
boolean[][] visited = new boolean[m][n];
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{0,0});//加入起点0,0
int res = 0;
while (!q.isEmpty()){
int[] cell = q.poll();
if(cell[0]>=m||cell[0]<0||cell[1]>=n||cell[1]<0||checkijk(cell[0],cell[1],k)||visited[cell[0]][cell[1]])
continue;//这个单元格不满足条件的情况
visited[cell[0]][cell[1]] = true;
res++;
q.offer(new int[]{cell[0]+1,cell[1]});
q.offer(new int[]{cell[0],cell[1]+1});
}
return res;
}
//检验数位和
private boolean checkijk(int i, int j, int k) {
int sum = 0;
while (i>0){
sum += (i % 10);
i /= 10;
}
while (j>0){
sum += (j % 10);
j /= 10;
}
return sum>k;
}
2. DFS
一般涉及二叉树、矩阵路径选择,树的子结构,树与树之间的匹配(路径匹配)等问题,联想DFS。DFS有三种遍历方式:先序、中序、后序。DFS实质上是一种递归思想,把问题分解成子问题。
2.1 基本框架
比较简单啦,就是先序、中序、后序遍历的框架。
public void dfs(TreeNode root){
//前序遍历——执行操作
dfs(root.left);
//中序
dfs(root.right)
//后序
}
2.2 例题
2.2.1 剑指offer 26. 树的子结构
题目描述
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。

输入
A = [1,2,3], B = [3,1]
输出
false
解题思路
判断B是不是A的子结构可以分解为两步:
- 以A为根节点的子树包含B;
- 以A.left为根节点的子树包含B;
- 以A.right为根节点的子树包含B;
特例处理:如果A为空或者B为空直接返回false。
所以递归的意思就出来了。关于如何判断以A为根节点的子树包含B,可以分三步(其实也就一个先序遍历):
- 判断A的值和B的值是否相等;
- 判断A的左节点和B的左节点是否相等;
- 判断A的左节点和B的左节点是否相等;
终止条件:
- 如果B为空说明匹配完了返回true;
- 如果A为空说明以及越过叶子节点了,没有匹配完返回false;
- 如果A节点的值不等于B节点的值说明匹配失败返回false;
这样子又一个递归关系就出来了。
代码
//dfs
public boolean isSubStructure(TreeNode A, TreeNode B) {
if(A==null||B==null)
return false;
return recur(A,B)||isSubStructure(A.left,B)||isSubStructure(A.right,B);
}
public boolean recur(TreeNode A,TreeNode B){
if(B==null)
return true;
if(A==null)
return false;
if(A.val!=B.val)
return false;
return recur(A.left,B.left)&&recur(A.right,B.right);
}
2.2.2 矩阵中的路径
题目描述
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
例如,在下面的 3×4 的矩阵中包含单词 “ABCCED”(单词中的字母已标出)。

输入
board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出
true
解题思路
一个直接想法就是遍历矩阵得出所有的字符串可能性。这边有两个遍历方法:DFS和BFS,DFS是先沿着一个方向搜到底然后再回溯到上一个节点继续搜索,DFS还有一个剪枝策略就是一边搜索一边匹配,如果遇到匹配不成功的情况就立即返回。
先要进行剪枝就要两个需要匹配的字符也就是board[i][j]和word[k]所以递归参数就是i,j,k。
- [i,j]先从[0,0]开始对应board[i][j] = ‘A’,word[k] = ‘A’,先向下搜索,发现不匹配,回溯;
- 再向上搜索,发现越界不匹配;
- 再向右搜索可以匹配,更新当前位置,并把该位置标记为已经访问;
- 继续沿着上、下、左、右搜索;
- 判断是否匹配(终止条件):a. 数组越界;b. 当前字符与word字符不一样;c. 当前矩阵元素已经访问过了。以上全部返回false。如果k == len(word)-1表示word中字符全部匹配完成,返回true。
一般来说递归要明确递归参数、递推工作以及终止条件,以上前4点就是递推工作最后一点就是终止条件。
代码
public boolean exist(char[][] board, String word) {
for(int i=0;i<board.length;i++){
for(int j = 0;j<board[i].length;j++){
if(dfs(board,word.toCharArray(),i,j,0)) return true;
}
}
return false;
}
public boolean dfs(char[][] board, char[] word, int i,int j,int k){
if(i>=board.length||i<0||j>=board[0].length||j<0||k>=word.length||board[i][j]!=word[k]) return false;//越界或者不匹配就返回false
if(k==word.length-1) return true;//匹配到了最后
char tmp = board[i][j];
board[i][j] = '\0';//搜索到的置空
boolean res = dfs(board,word,i+1,j,k+1)||dfs(board,word,i-1,j,k+1)
||dfs(board,word,i,j+1,k+1)||dfs(board,word,i,j-1,k+1);//向四周搜索看看有没有匹配的
board[i][j] = tmp;//搜索完回溯
return res;
}
2.2.3 剑指 Offer 34. 二叉树中和为某一值的路径
题目描述
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
示例
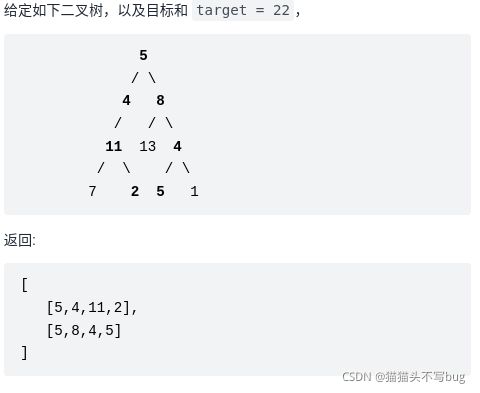
解题思路
一看就是DFS吧,遍历二叉树所有路径看是否有满足条件的路径。
- 递归参数:当前根节点以及target
- 递推工作:
- 先把当前节点的值加入路径序列,并更新target
- 如果到达叶子节点且target==0,就把该条路径返回
- 向左搜索路径
- 向右搜索路径
终止条件:当前为null,表示搜索完成。
记住要向前回溯,就是向左搜完要回到根节点再向右边搜索。对应操作就是清空路径序列。
代码
List<List<Integer>> res = new LinkedList<>();
Deque<Integer> route = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int target) {
dfs(root,target);
return res;
}
//dfs+回溯
public void dfs(TreeNode node,int target){
if(node==null)
return;
route.offerLast(node.val);//先把该节点加到路径
target -= node.val;
//如果到达叶子节点且满足target就返回
if(node.left==null&&node.right==null&&target==0){
res.add(new LinkedList<>(route));
}
dfs(node.left,target);
dfs(node.right,target);
route.pollLast();//回溯
}
这边可以再提一下二叉树回溯框架:
public void backtrack(TreeNode root){
if(满足终止条件){
return;
}
//加入选择
route.add(root);
//状态更新
backtrack(root.left);
backtrack(root.right);
//选择撤销
route.remove(root);
}