迷宫-深度优先搜索-打印所有可行路径
继上一篇“迷宫-广度优先搜索-最短路径并打印该条最短路径”——https://mp.csdn.net/postedit/103229718,想着如何才能把所有可行路径打印出来,网上看了些资料都是推荐使用深度优先搜索方法,但是没看到过完全的实现,因此有了这次自己记录。
目录
1.本文例子的迷宫如下:
2.深度优先的基本思路-
3.只考虑一条路径的实现
(1) 栈代码
(2)深度遍历代码
(3)运行结果
4.打印所有路径
(1)从3容易想的是以下2点
(2)代码
(3)运行结果
5.节点的遍历方向及节点出栈时恢复该节点的标记
(1)分析
(2)最终思路
(3)对节点已搜索的方向及点已在栈中的状态如何标记
(4)标记代码
(5)打印所有路径的深度搜索代码
6.源码链接
1.本文例子的迷宫如下:
起点(0,0),需要打印到终点(2,3)的所有可行路径?
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
| 0 |
0 |
1 |
0 |
上篇提到如果是只要求最短路径并打印推荐使用广度优先,求所有路径使用深度优先比较好。下面是一层层的加深思考
2.深度优先的基本思路-
一条道到黑,走不下去了立即回头。
1.起始点入栈,访问栈顶并寻找下一个合适的点,节点合法就入栈并用DP数组标记,1表示已在栈中(已遍历过)
2.继续1,一直循环直到该点找不到合适的下一个状态点就出栈返回上一层,直到栈为空结束遍历
3.只考虑一条路径的实现
用2的思路其实实现一条路径并打印其实是非常简单的,但是还是要手写栈,或者递归方式,本人暂时不喜欢用递归。
(1) 栈代码
/*栈开始*/
typedef struct Stack_
{
int cap;
int top;
int** data;
}STACK_S;
void Stack_Init(STACK_S* stack,int cap,int size)
{
int i = 0;
stack->cap = cap;
stack->top = -1;
stack->data = (int**)malloc(sizeof(int*)*cap);
for(i = 0; i <= cap -1 ;i++)
{
stack->data[i] = (int*)malloc(sizeof(int)*size);
memset(stack->data[i],0,sizeof(int)*size);
}
}
int Stack_Is_Full(STACK_S* stack)
{
return (stack->top == stack->cap) ? 1 : 0;
}
int Stack_Is_Empty(STACK_S* stack)
{
return (stack->top == -1) ? 1 : 0;
}
void Stack_Pushback(STACK_S* stack,int x,int y)
{
if(Stack_Is_Full(stack) != 1)
{
stack->top++;
stack->data[stack->top][0] = x;
stack->data[stack->top][1] = y;
}
}
int* Stack_GetTop(STACK_S* stack)
{
if(Stack_Is_Empty(stack) != 1)
{
return stack->data[stack->top];
}
else
return NULL;
}
void Stack_Pop(STACK_S* stack)
{
if(Stack_Is_Empty(stack) != 1)
{
stack->top--;
}
}
/******************栈结束***************/(2)深度遍历代码
/*打印栈中的路径**/
void printf_stack_path(STACK_S* stack)
{
STACK_S stack_temp = {0};
int* data = NULL;
Stack_Init(&stack_temp,stack->cap,2);
//把栈给放到另一个栈
while(Stack_Is_Empty(stack) != 1)
{
data = Stack_GetTop(stack);
Stack_Pushback(&stack_temp,data[0],data[1]);
Stack_Pop(stack);
}
while(Stack_Is_Empty(&stack_temp) != 1)
{
data = Stack_GetTop(&stack_temp);
printf("(%d,%d)->",data[0],data[1]);
Stack_Pushback(stack,data[0],data[1]);
Stack_Pop(&stack_temp);
}
//退格把最后一个"->"去掉
printf("\b\b\t\n");
}
void Maze_Dfs_All_Path(int** maze,int max_x,int max_y,int* start,int* end,STACK_S* stack,int** dp)
{
int i = 0;
int next_x = 0,next_y = 0;
int *cur = 0;
int pre_x = -1,pre_y = -1;
//起点入栈并标记
Stack_Pushback(stack,start[0],start[1]);
*(((int*)dp)+max_y*start[0]+start[1]) = 1;
while(Stack_Is_Empty(stack) != 1)
{
cur = Stack_GetTop(stack);
//printf("cur:(%d,%d)\n",cur[0],cur[1]);
for(i =0; i <= MAX_DIR -1;i++ )
{
next_x = cur[0]+s_dirs[i][0];
next_y = cur[1]+s_dirs[i][1];
//printf("next:(%d,%d)\n",next_x,next_y);
if(Point_Is_Boundry(max_x,max_y,next_x,next_y) == 1)//不能是边界意外
continue;
if( *(((int*)maze)+max_y*next_x+next_y) == 1)//不能是墙
continue;
if(*(((int*)dp)+max_y*next_x+next_y) == 1)//不能被标记,及已经在栈中了
{
//printf("dp is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//printf("now (%d,%d) push back\n",next_x,next_y);
Stack_Pushback(stack,next_x,next_y);
*(((int*)dp)+max_y*next_x+next_y) = 1;
if(next_x == end[0] && next_y == end[1])
{
printf_stack_path(stack);
return;
}
else
break;
}
if(i >= MAX_DIR)
Stack_Pop(stack);
}
}(3)运行结果
![]()
4.打印所有路径
(1)从3容易想的是以下2点
a.在找到终点时,不能return而是应该continue
b.continue前应将顶点出栈,并需要设置成非标记状态并,否则下次遇到终点,终点由于被标记无法入栈
(2)代码
void Maze_Dfs_All_Path(int** maze,int max_x,int max_y,int* start,int* end,STACK_S* stack,int** dp)
{
int i = 0;
int next_x = 0,next_y = 0;
int *cur = 0;
int pre_x = -1,pre_y = -1;
//起点入栈并标记
Stack_Pushback(stack,start[0],start[1]);
*(((int*)dp)+max_y*start[0]+start[1]) = 1;
while(Stack_Is_Empty(stack) != 1)
{
cur = Stack_GetTop(stack);
//printf("cur:(%d,%d)\n",cur[0],cur[1]);
for(i =0; i <= MAX_DIR -1;i++ )
{
next_x = cur[0]+s_dirs[i][0];
next_y = cur[1]+s_dirs[i][1];
//printf("next:(%d,%d)\n",next_x,next_y);
if(Point_Is_Boundry(max_x,max_y,next_x,next_y) == 1)//不能是边界意外
continue;
if( *(((int*)maze)+max_y*next_x+next_y) == 1)//不能是墙
continue;
if(*(((int*)dp)+max_y*next_x+next_y) == 1)//不能被标记,及已经在栈中了
{
//printf("dp is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//printf("now (%d,%d) push back\n",next_x,next_y);
Stack_Pushback(stack,next_x,next_y);
*(((int*)dp)+max_y*next_x+next_y) = 1;
if(next_x == end[0] && next_y == end[1])
{
printf_stack_path(stack);
//终点出栈如果不进行恢复标记的话,下一次就不会进了
*(((int*)dp)+max_y*end[0]+end[1]) = 0;
Stack_Pop(stack);
continue;
}
else
break;
}
if(i >= MAX_DIR)
Stack_Pop(stack);
}
}
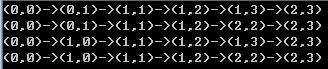
(3)运行结果
期望结果
实际结果
原因分析
可看出其实是少了2条路径的,打开代码中那些printf可以看到其实在(0,0)->(0,1) ->(1,1)时,访问栈顶(1,1)然后按照左、右、上、下的顺序,下一节点(1,0)入栈结果发现(1,0)这个节点的四个方向的下一个节点都不合法,导致(1,0)出栈,但是(1,0)已经被DP标记,所以导致在找完前2条路径后弹栈,知道栈顶为(0,0)时,开始“左、右、上、下”发现(1,0)已经被标记
5.节点的遍历方向及节点出栈时恢复该节点所有标记
(1)分析
由4中原因可以看出,当一个节点在栈中被弹出后他的“在栈标记”应该被取消,否则会导致路径遗漏。但是如果不考虑方向的情况下,(0,0)->(0,1) ->(1,1)->(1,0)当(1,0)被弹出后标记被取消,那么栈顶(1,1)又会从4个方向去遍历,从而又将(1,0)入栈,从而死循环。
因此弹栈取消“在栈标记”引出的新问题可以通过“方向标记”来避免进入死循环,即(1,1)向左遍历到(1,0)可入栈时,(1,1)节点的左遍历方向应该被标记。
(2)最终思路
a.根几点入栈,从四个方向中未被标记的方向搜寻合法的下一个状态(节点),如果合法,栈顶节点方向需要标记,下一节点的“在栈标记”被标记
b.继续访问栈顶,重复上一步骤,如果栈顶节点没有合法的下一个节点,则栈顶出栈,并将栈顶的“在栈标记取消”,【其实在栈标记是为了下一节点成为栈顶元素时不会反向遍历】,出栈取消可以避免路径遗漏;当然“方向标记”也要取消,否则即使该节点下次重新入栈成为栈顶,也不会起作用,因为方向标记全是已标记
c.期间如果下一个状态是终点,则调用打印路径函数打印,之后终点也当一般栈顶处理,出栈并取消标记
(3)对节点已搜索的方向及点已在栈中的状态如何标记
本代码中用DP数组的元素的bit0-3分表标识该节点的左右上下四个方向标记,bit4标识“在栈标记”
(4)标记代码
//判断DP的某个bit是否为1,比如查在栈标记IS_DP_BITN_TRUE(DP[0][1],4)
#define IS_DP_BITN_TRUE(value,bitn) ((value) >> (bitn)) & 0x1
//设置DP的某个bit为1或者0
#define SET_DP_BITN(value,bitn,flag) \
if((flag) == 1)\
{\
(value) = ((value) | (0x1 << bitn));\
}\
else\
(value) = ((value) & (~(0x1<(5)打印所有路径的深度搜索代码
tips:取消printf的注释可以显示节点进出站栈过程
void Maze_Dfs_All_Path(int** maze,int max_x,int max_y,int* start,int* end,STACK_S* stack,int** dp)
{
int i = 0;
int next_x = 0,next_y = 0;
int *cur = 0;
int pre_x = -1,pre_y = -1;
//起点入栈
Stack_Pushback(stack,start[0],start[1]);
SET_DP_BITN(*(((int*)dp)+max_y*start[0]+start[0]),4,1);
while(Stack_Is_Empty(stack) != 1)
{
cur = Stack_GetTop(stack);
//printf("cur:(%d,%d)\n",cur[0],cur[1]);
for(i =0; i <= MAX_DIR -1;i++ )
{
next_x = cur[0]+s_dirs[i][0];
next_y = cur[1]+s_dirs[i][1];
//printf("next:(%d,%d)\n",next_x,next_y);
if(Point_Is_Boundry(max_x,max_y,next_x,next_y) == 1)
{
//printf("Boundry:(%d,%d)\n",next_x,next_y);
continue;
}
if( *(((int*)maze)+max_y*next_x+next_y) == 1)
{
//printf("maze is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//如果下一个节点已经标记,则不合法继续寻找下一个方向
if(IS_DP_BITN_TRUE(*(((int*)dp)+max_y*next_x+next_y),4))
{
//printf("dp is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//如果本节点方向已经被遍历则不继续
if(IS_DP_BITN_TRUE(*(((int*)dp)+max_y*cur[0]+cur[1]),i))
{
//printf("(%d,%d) 的 %d 方向已经遍历\n",cur[0],cur[1],i);
continue;
}
//printf("now (%d,%d) push back\n",next_x,next_y);
Stack_Pushback(stack,next_x,next_y);
//设置下一节点为已经访问,以及本节点的方向
SET_DP_BITN(*(((int*)dp)+max_y*next_x+next_y),4,1);
SET_DP_BITN(*(((int*)dp)+max_y*cur[0]+cur[1]),i,1);
if(next_x == end[0] && next_y == end[1])
{
printf_stack_path(stack);
//终点出栈如果不进行恢复标记的话,下一次就不会进了
Stack_Pop(stack);
CLEAR_DP_ALL(*(((int*)dp)+max_y*end[0]+end[1]));
continue;
}
else
break;
}
if(i >= MAX_DIR)
{
CLEAR_DP_ALL(*(((int*)dp)+max_y*cur[0]+cur[1]));
//printf("(%d,%d) pop and clear all dp bit,dp %d\n",cur[0],cur[1],*(((int*)dp)+max_y*cur[0]+cur[1]));
Stack_Pop(stack);
}
}
}6.源码链接
PS:长度只需要在打印时统计栈中节点个数其实就可以,文中代码这部分未做
1.只求一条路径并打印长度:https://pan.baidu.com/s/1ZgL2bPIv6koNfoChBdJkwQ
2.打印所有路径:https://pan.baidu.com/s/1064x3hyQ23scaAho7e9Cbw
#include
#include
#include
/*大概的思路是:
1.找到一个合适的点(非边界,非标记)就入栈,访问栈顶,直到该栈顶找不到下一个点才出栈,返回上一层
2.入栈时需要进行标记,当找到终点时同样入栈,并调用打印函数,把这个终点出栈并恢复标记即可即可,继续搜索
其实需要考虑如下场景
0 0 0
0 0 0
1 0 0
路线(0,0)->(0,1)->(1,1)->(1,0)时,此时会对栈顶(1,0)进行4个方向的遍历,发现往左不行,往右已经被标记,往上也被标记,往下不行,
此时出栈,但是没有恢复比标记,当一直出栈到(0,0)发现往下元素本来合法的但是因为被标记导致(0,0)->(1,0)->(1,1)路线被堵顶,
所以需要增加如下方式:即对于一个当前的顶点,如果他的四个方向都没有遍历的话*/
#define MAZE_MAX_X 4
#define MAZE_MAX_Y 4
#define MAX_DIR 4
#define DIM 2
#define IS_DP_BITN_TRUE(value,bitn) ((value) >> (bitn)) & 0x1
#define SET_DP_BITN(value,bitn,flag) \
if((flag) == 1)\
{\
(value) = ((value) | (0x1 << bitn));\
}\
else\
(value) = ((value) & (~(0x1<cap = cap;
stack->top = -1;
stack->data = (int**)malloc(sizeof(int*)*cap);
for(i = 0; i <= cap -1 ;i++)
{
stack->data[i] = (int*)malloc(sizeof(int)*size);
memset(stack->data[i],0,sizeof(int)*size);
}
}
int Stack_Is_Full(STACK_S* stack)
{
return (stack->top == stack->cap) ? 1 : 0;
}
int Stack_Is_Empty(STACK_S* stack)
{
return (stack->top == -1) ? 1 : 0;
}
void Stack_Pushback(STACK_S* stack,int x,int y)
{
if(Stack_Is_Full(stack) != 1)
{
stack->top++;
stack->data[stack->top][0] = x;
stack->data[stack->top][1] = y;
}
}
int* Stack_GetTop(STACK_S* stack)
{
if(Stack_Is_Empty(stack) != 1)
{
return stack->data[stack->top];
}
else
return NULL;
}
void Stack_Pop(STACK_S* stack)
{
if(Stack_Is_Empty(stack) != 1)
{
stack->top--;
}
}
/******************栈结束***************/
int Point_Is_Boundry(int max_x,int max_y,int x,int y)
{
if(x < 0 || x >= max_x || y < 0 || y >= max_y)
return 1;
return 0;
}
/*打印栈中的路径**/
void printf_stack_path(STACK_S* stack)
{
STACK_S stack_temp = {0};
int* data = NULL;
Stack_Init(&stack_temp,stack->cap,2);
//把栈给放到另一个栈
while(Stack_Is_Empty(stack) != 1)
{
data = Stack_GetTop(stack);
Stack_Pushback(&stack_temp,data[0],data[1]);
Stack_Pop(stack);
}
while(Stack_Is_Empty(&stack_temp) != 1)
{
data = Stack_GetTop(&stack_temp);
printf("(%d,%d)->",data[0],data[1]);
Stack_Pushback(stack,data[0],data[1]);
Stack_Pop(&stack_temp);
}
//退格把最后一个"->"去掉
printf("\b\b\t\n");
}
void Maze_Dfs_All_Path(int** maze,int max_x,int max_y,int* start,int* end,STACK_S* stack,int** dp)
{
int i = 0;
int next_x = 0,next_y = 0;
int *cur = 0;
int pre_x = -1,pre_y = -1;
//起点入栈
Stack_Pushback(stack,start[0],start[1]);
SET_DP_BITN(*(((int*)dp)+max_y*start[0]+start[0]),4,1);
while(Stack_Is_Empty(stack) != 1)
{
cur = Stack_GetTop(stack);
//printf("cur:(%d,%d)\n",cur[0],cur[1]);
for(i =0; i <= MAX_DIR -1;i++ )
{
next_x = cur[0]+s_dirs[i][0];
next_y = cur[1]+s_dirs[i][1];
//printf("next:(%d,%d)\n",next_x,next_y);
if(Point_Is_Boundry(max_x,max_y,next_x,next_y) == 1)
{
//printf("Boundry:(%d,%d)\n",next_x,next_y);
continue;
}
if( *(((int*)maze)+max_y*next_x+next_y) == 1)
{
//printf("maze is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//如果下一个节点已经标记,则不合法继续寻找下一个方向
if(IS_DP_BITN_TRUE(*(((int*)dp)+max_y*next_x+next_y),4))
{
//printf("dp is 1 (%d,%d)\n",next_x,next_y);
continue;
}
//如果本节点方向已经被遍历则不继续
if(IS_DP_BITN_TRUE(*(((int*)dp)+max_y*cur[0]+cur[1]),i))
{
//printf("(%d,%d) 的 %d 方向已经遍历\n",cur[0],cur[1],i);
continue;
}
//printf("now (%d,%d) push back\n",next_x,next_y);
Stack_Pushback(stack,next_x,next_y);
//设置下一节点为已经访问,以及本节点的方向
SET_DP_BITN(*(((int*)dp)+max_y*next_x+next_y),4,1);
SET_DP_BITN(*(((int*)dp)+max_y*cur[0]+cur[1]),i,1);
if(next_x == end[0] && next_y == end[1])
{
printf_stack_path(stack);
//终点出栈如果不进行恢复标记的话,下一次就不会进了
Stack_Pop(stack);
CLEAR_DP_ALL(*(((int*)dp)+max_y*end[0]+end[1]));
continue;
}
else
break;
}
if(i >= MAX_DIR)
{
CLEAR_DP_ALL(*(((int*)dp)+max_y*cur[0]+cur[1]));
//printf("(%d,%d) pop and clear all dp bit,dp %d\n",cur[0],cur[1],*(((int*)dp)+max_y*cur[0]+cur[1]));
Stack_Pop(stack);
}
}
}
int main()
{
int len = 0, i =0,j = 0;
//bit0:1:2:3分别表示左右前后的标志位,bit4表示是否标记被访问
int dp[MAZE_MAX_X][MAZE_MAX_Y] = {0};
int maze[MAZE_MAX_X][MAZE_MAX_Y] = {
{0,0,1,0},
{0,0,0,0},
{1,1,0,0},
{0,0,1,0},
};
//起点、终点
int start[2] = {0,0};
int end[2] = {2,3};
STACK_S stack = {0};
Stack_Init(&stack,100,2);
memset((int*)dp,0,sizeof(int)*MAZE_MAX_X*MAZE_MAX_Y);
Maze_Dfs_All_Path((int**)maze,MAZE_MAX_X,MAZE_MAX_Y,start,end,&stack,(int**)dp);
return 0;
}