图的遍历(深度优先搜索法和广度优先搜索法)
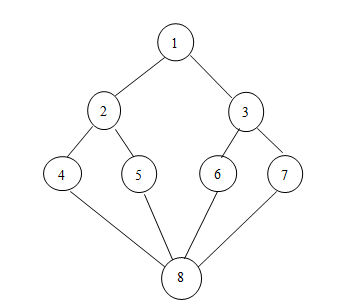
 深度搜索
深度搜索
//
----------------------------------------------------------------
//
图的深度优先搜索法
//
----------------------------------------------------------------
#include
"
iostream
"
#include
"
stdlib.h
"
using
namespace
std;
struct
node
//
图顶点结构声明
{
int
vertex;
//
顶点数据
struct
node
*
nextnode;
//
指下一顶点的指针
};
typedef
struct
node
*
graph;
//
图的结构新类型
struct
node head[
9
];
//
图的顶点结构数组
int
visited[
9
];
//
顶点记录数组
//
-----------------------------------------------------------------
//
创建图
//
-----------------------------------------------------------------
void
creategraph(
int
*
node,
int
num)
{
graph newnode;
//
新顶点指针
graph ptr;
int
from;
//
边的起点
int
to;
//
边的终点
int
i;
for
(i
=
0
;i
<
num;i
++
)
//
读取边的循环
{
from
=
node[i
*
2
];
//
边的起点
to
=
node[i
*
2
+
1
];
//
边的终点
//
-----------------创建新顶点内存------------------------------
newnode
=
(graph) malloc(
sizeof
(
struct
node));
newnode
->
vertex
=
to;
//
创建顶点内容
newnode
->
nextnode
=
NULL;
//
设置指针初值
ptr
=&
(head[from]);
//
顶点位置
while
(ptr
->
nextnode
!=
NULL)
//
遍历至链表尾
ptr
=
ptr
->
nextnode;
//
下一个顶点
ptr
->
nextnode
=
newnode;
//
插入结尾
}
}
//
------------------------------------------------------------------------
//
图的深度优先搜索
//
------------------------------------------------------------------------
void
dfs(
int
current)
{
graph ptr;
visited[current]
=
1
;
//
记录已遍历过
printf(
"
顶点[%d]
"
,current);
//
输出遍历顶点值
ptr
=
head[current].nextnode;
//
顶点位置
while
(ptr
!=
NULL)
//
遍历至链表尾
{
if
(visited[ptr
->
vertex]
==
0
)
//
如果没遍历过
dfs(ptr
->
vertex);
//
递归遍历调用
ptr
=
ptr
->
nextnode;
//
下一个顶点
}
}
//
----------------将遍历内容输出------------------------
int
main()
{
graph ptr;
int
node[
20
][
2
]
=
{
//
边数组
{
1
,
2
},{
2
,
1
},
{
1
,
3
},{
3
,
1
},
{
2
,
4
},{
4
,
2
},
{
2
,
5
},{
5
,
2
},
{
3
,
6
},{
6
,
3
},
{
3
,
7
},{
7
,
3
},
{
4
,
8
},{
8
,
4
},
{
5
,
8
},{
8
,
5
},
{
6
,
8
},{
8
,
6
},
{
7
,
8
},{
8
,
7
} };
int
i;
for
(i
=
1
;i
<=
8
;i
++
)
{
head[i].vertex
=
i;
//
设置顶点值
head[i].nextnode
=
NULL;
//
清除图指针
visited[i]
=
0
;
//
设置遍历初值
}
creategraph(
*
node,
20
);
//
创建图
printf(
"
图的邻接表内容:\n
"
);
for
(i
=
1
;i
<=
8
;i
++
)
{
printf(
"
顶点%d=>
"
,head[i].vertex);
//
顶点值
ptr
=
head[i].nextnode;
//
顶点位置
while
(ptr
!=
NULL)
//
遍历至链表尾
{
printf(
"
%d
"
,ptr
->
vertex);
//
输出顶点内容
ptr
=
ptr
->
nextnode;
//
下一个顶点
}
printf(
"
\n
"
);
}
printf(
"
图的深度优先遍历内容: \n
"
);
dfs(
1
);
printf(
"
\n
"
);
}
 广度搜索
广度搜索
//
----------------------图的广度优先搜索------------------------
#include
"
iostream
"
#include
"
stdlib.h
"
#define
MAXQUEUE 10
//
队列的最大容量
using
namespace
std;
struct
node
//
图顶点结构声明
{
int
vertex;
//
顶点数据
struct
node
*
nextnode;
//
指向下一顶点的指针
};
typedef
struct
node
*
graph;
//
图的结构新类型
struct
node head[
9
];
//
图的顶点结构数组
int
visited[
9
];
//
遍历记录数组
int
queue[MAXQUEUE];
//
队列数组声明
int
front
=-
1
;
//
队列的对头
int
rear
=-
1
;
//
队列的队尾
//
---------------------创建图-----------------------
void
creategraph(
int
*
node,
int
num)
{
graph newnode;
//
新顶点指针
graph ptr;
int
from;
//
边的起点
int
to;
//
边的终点
int
i;
for
(i
=
0
;i
<
num;i
++
)
//
读取边的循环
{
from
=
node[i
*
2
];
//
边的起点
to
=
node[i
*
2
+
1
];
//
边的终点
//
-----------创建新顶点内存---------------------
newnode
=
( graph ) malloc(
sizeof
(
struct
node));
newnode
->
vertex
=
to;
//
创建顶点内容
newnode
->
nextnode
=
NULL;
//
设置指针初值
ptr
=&
(head[from]);
//
顶点位置
while
(ptr
->
nextnode
!=
NULL)
//
遍历至链表尾
ptr
=
ptr
->
nextnode;
//
下一个顶点
ptr
->
nextnode
=
newnode;
//
插入结尾
}
}
//
-----------------------队列的数据存入-------------------------
int
enqueue(
int
value)
{
if
(rear
>=
MAXQUEUE)
//
检查队列是否全满
return
-
1
;
//
无法存入
rear
++
;
//
队尾指针往前移
queue[rear]
=
value;
//
存入队列
}
//
-----------------------队列数据的取出-----------------------
int
dequeue()
{
if
(front
==
rear)
//
检查队列是否为空
return
-
1
;
//
无法取出
front
++
;
//
对头指针往前移
return
queue[front];
//
队列取出
}
//
-------------------------图的广度优先搜索法--------------------------------
void
bfs(
int
current)
{
graph ptr;
//
处理第一个顶点
enqueue(current);
//
将顶点存入队列
visited[current]
=
1
;
//
记录已遍历过
printf(
"
顶点[%d]
"
,current);
//
输出遍历顶点值
while
(front
!=
rear )
//
队列是否为空
{
current
=
dequeue();
//
将顶点从队列中取出
ptr
=
head[current].nextnode;
//
顶点位置
while
(ptr
!=
NULL)
//
遍历至链表尾
{
if
(visited[ptr
->
vertex]
==
0
)
//
如果没有遍历过
{
enqueue(ptr
->
vertex);
//
递归遍历调用
visited[ptr
->
vertex]
=
1
;
//
记录已遍历过
printf(
"
顶点[%d]
"
,ptr
->
vertex);
}
ptr
=
ptr
->
nextnode;
//
下一个顶点
}
}
}
//
-----------------将遍历内容输出-----------------------
int
main()
{
graph ptr;
int
node[
20
][
2
]
=
{
//
边数组
{
1
,
2
},{
2
,
1
},
{
1
,
3
},{
3
,
1
},
{
2
,
4
},{
4
,
2
},
{
2
,
5
},{
5
,
2
},
{
3
,
6
},{
6
,
3
},
{
3
,
7
},{
7
,
3
},
{
4
,
8
},{
8
,
4
},
{
5
,
8
},{
8
,
5
},
{
6
,
8
},{
8
,
6
},
{
7
,
8
},{
8
,
7
} };
int
i;
for
(i
=
1
;i
<=
8
;i
++
)
{
head[i].vertex
=
i;
//
设置顶点值
head[i].nextnode
=
NULL;
//
清除图指针
visited[i]
=
0
;
//
设置遍历初值
}
creategraph(
*
node,
20
);
//
创建图
printf(
"
图的邻接表内容:\n
"
);
for
(i
=
1
;i
<=
8
;i
++
)
{
printf(
"
顶点%d =>
"
,head[i].vertex);
//
顶点值
ptr
=
head[i].nextnode;
//
顶点位置
while
(ptr
!=
NULL)
//
遍历至链表尾
{
printf(
"
%d
"
,ptr
->
vertex);
//
输出顶点内容
ptr
=
ptr
->
nextnode;
//
下一个顶点
}
printf(
"
\n
"
);
}
printf(
"
图的广度优先遍历内容: \n
"
);
bfs(
1
);
printf(
"
\n
"
);
}
