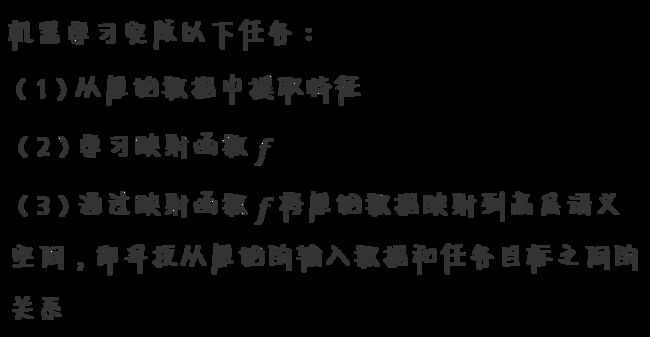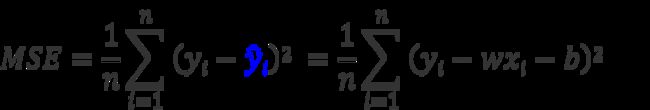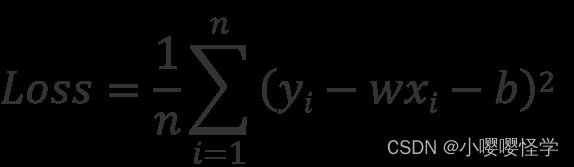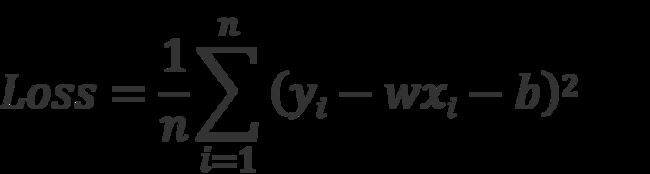机器学习||机器学习发展&人工智能 VS 机器学习 VS 深度学习一种新的编程范&机器学习机器学习分类&分类&回归&聚类$&降维&机器学习术语&机器学习的三个要素步骤假设空间\评价指标\优化目标寻解算
目录
一、机器学习发展
二、人工智能 VS 机器学习 VS 深度学习
三、机器学习
1.机器学习:一种新的编程范式
2.机器学习任务
四、机器学习分类
1.分类
2.回归
3.聚类
4.降维
五、机器学习术语
六、机器学习的三个要素(步骤)
1、假设空间
2、评价指标(优化目标)
3、优化目标寻解算法
小结:
一、机器学习发展
AlphaGo、无人驾驶、模式、语音识别等的突破性进展,人工智能得到了快速发展。作为人工智能的核心,机器学习(ML)备受瞩目。如今,机器学习的应用已遍及人工智能的各个分支,如专家系统、自动推理、自然语言理解、模式识别、计算机视觉、智能机器人等领域。
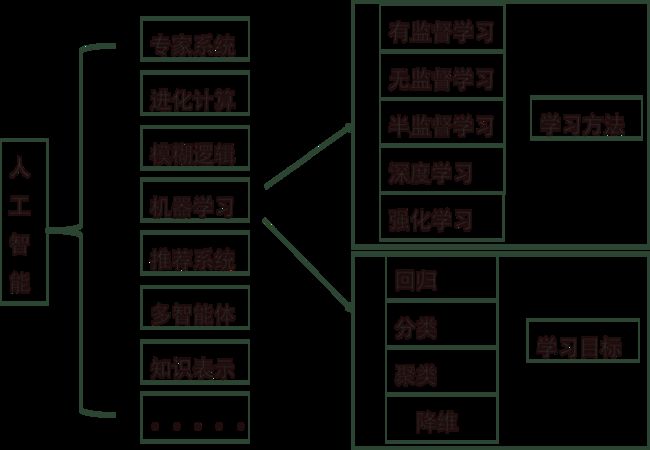
二、人工智能 VS 机器学习 VS 深度学习
人工智能、机器学习和深度学习三者之间的关系?
三者覆盖的技术范畴是逐层递减的,人工智能是最宽泛的概念。机器学习是实现人工智能的手段和方法。有些是可以不用机器学习的算法进行智能化的运算。
机器学习:专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能。
深度学习是机器学习算法中最热的一个分支,在近些年取得了显著的进展,并代替了多数传统机器学习算法。
三、机器学习
简而言之,机器的“学习”,是通过以往的经验,即历史数据(经验),学习数据内部的逻辑模型,并将学到的模型应用在新数据上,进行预测。
根据经验 E 来提高性能指标 P 的过程是一个典型的最优化过程。数学中各种最优化的理论都可以应用其中:演绎、归纳和演化。
优化模型(optimization model)是在给定条件下寻找最佳方案的模型。
最佳的含义有各种各样:成本最小、收益最大、利润最多、距离最短、时间最少、空间最小等,即在资源给定时寻找最好的目标,或在目标确定下使用最少的资源
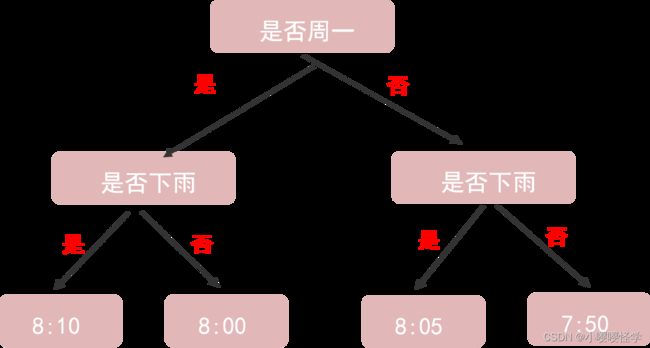
这张图就是一张简单的机器学习模型,称为决策树模型。
机器学习通常是从已知数据中去学习数据中蕴含的规律或者判断规则,从数据中训练出模型,然后通过迭代学习去不断优化模型,把学到的模型应用到未来的新数据上并作出判断或预测。
机器学习中的“训练”与“预测”过程可以对应到人类的“归纳”和“推测”过程。
所谓归纳,是指通过对特例的分析来引出普遍结论的一种推理形式。演绎则是从一般到个别。
机器学习中的每一种算法,究其根本,都是一种数学表达。无论是机器学习,还是深度学习,都是试图找到一个函数 。
这个函数可以简单,可以复杂,函数的表达并不重要,只是一个工具。重要的是这个函数能够尽可能准确的拟合出输入数据和输出结果间的关系。比如语音识别、图像识别、下围棋,人机问答系统。
1.机器学习:一种新的编程范式
在经典的程序设计中,人们输入的是规则(即程序)和需要根据这些规则进行处理的数据,系统输出的是答案。
机器学习:人们输入的是数据和从这些数据中预期得到的答案,系统输出的是规则。这些规则随后可应用于新的数据,并使计算机自主生成答案。
2.机器学习任务
四、机器学习分类
机器学习算法可以分为四类: 分类、回归、聚类、降维
1.分类
在机器学习中,分类问题中的某个类别叫作类(class)。数据点叫作样本(sample)。某个样本对应的类叫作标签(label)。
图中的每一个点代表一个样本,而一个样本由一组数据构成。这些数据 (X) 实际上都有一个标签 (Y) 。 Y 的值要么是圆,要么是三角。
分类 算法就是根据已知这些数据 (X) 的分类 (Y),找到这个边界。一旦进来一批新的没有标签的数据 (X) ,那么可以根据这个算法把这些数据 (X) 要么归类到圆,要么归类到三角。
例如:垃圾邮件分类(二分类)
2.回归
回归用于预测输入变量(自变量)和输出变量(因变量)之间的关系。特别是当输入变量的值发生变化时,输出变量值随之发生变化。
通过这些样本点拟合出来一条直线(曲线),称为回归曲线。这条线就是通过机器学习得到的。
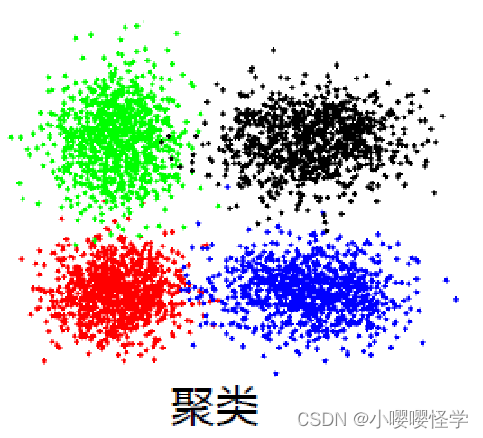
3.聚类
不管分类还是回归,都要有一个标签(label)。而聚类是没有标签的数据。输入被划分为若干个事先未知的组。通过一个算法学习,把它们归纳出几类。但并不知道这一类代表哪一类,因为事先数据没有标签。
4.降维
降维是机器学习另一个重要的领域。特征的维数过高, 会增加训练的负担与存储空间, 降维就是希望去除特征的冗余, 用更加少的维数来表示特征,降维是试图压缩数据的维度,通过降维算法,可以将具有几千个特征的数据压缩至若干个特征。降维主要用于数据压缩、数据可视化。例如将 5 维的数据压缩至 2 维,然后可以用二维平面来可视。奥卡姆剃刀定律(Occam’s Razor):“如无必要,勿增实体”,即“简单有效原理”。
五、机器学习术语
训练样本:即历史数据,相当于平时的各种学习资料和练习,目的是帮助提升学习能力。
测试样本:类似于考试试卷,检测学习成绩。
标签:可以认为是习题和考试的 标准答案。
特征:每个样本包含的多个属性(多维数据)被称作“特征”。
六、机器学习的三个要素(步骤)
1、假设空间
下表给出了夏威夷岛的一个火山从 1970-2005 年每五年的二氧化碳浓度,单位是百万分比浓度
按照这个规律,请预测一下 1982、2003、2015、2020 年的二氧化碳浓度?
存在两个变量:年份和二氧化碳浓度
把年份和二氧化碳浓度之间的关系可视化
假设:年份和二氧化碳浓度关系符合线性关系
采用线性回归模型,即拟合函数 f :
xi 是自变量,代表年份。 (yi) ̂ 是二氧化碳浓度预测值
2、评价指标(优化目标)
参数 , b 有无数组取值? 不同的值可以得到不同的直线方程 f
对于线性方程来说,最优的一组 , b 参数应该使拟合出的 预测值 (y ̂i) 与 观测值 ( yi ) 之差的平方和最小。该值也叫做:均方误差平方和(Mean Squared Error,MSE)。均方误差平方和函数也称为损失函数( Loss ),也就是给出的优化目标。
Loss 最小,就是找到的最好的一个假设函数 f。
Loss 函数的选择标准:
合理性:设计优化目标符合假设场景 。
易解性:能够快速找出在这个优化目标下最佳的那个假设函数 f
3、优化目标寻解算法
Loss 和参数 (w,b) 是函数关系,当 Loss 最小时, (w,b) 参数取值是多少?
在假设空间里,如何把最好的、最符合评价指标的假设函数快速找出来?
需要一个最优的寻解算法!
小结:
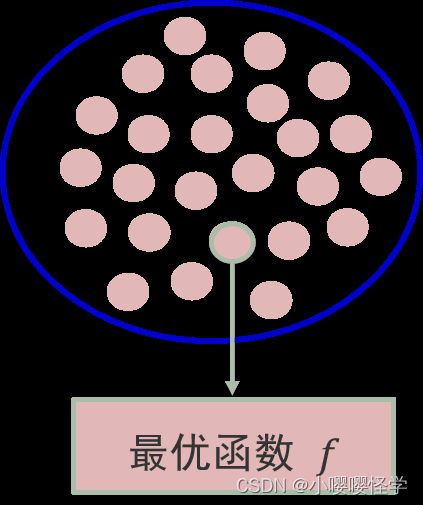
圆就是机器学习就是首先确定一个假设空间 圈。
需要设计一个优化目标(评价指标)来确定这个圆圈里假设函数 f 哪个好与不好。
最后,找到一个寻解算法,从这个圆圈里快速高效找到使得评价指标最好的那个假设函数 f ,即优化目标达到最优的 Y−X 关系。
注意:通过上述三个步骤,目前机器学习到的最好的假设,仅仅是在历史样本空间中观测最好的