国科大模式识别与机器学习2015-2019、2021仅考题

2015

1. （8）试描述线性判别函数的基本概念，并说明既然有线性判别函，为什么还需要非线性判别函数？假设有两种模式，每类包括6个4维不同的模式，且良好分布。如果他们是线性可分的。问权向量至少需要几个系数分量？假如要建立额尔茨的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变）

2. (8分)简述偏差方差分解及其推导过程，并说明偏差、方差、噪声三部分的内在含义。

3. (8 分) 试描述用 EM 算法求解高斯混合模型的思想和过程，并分析 k-means 和高斯混合模型在求解聚类问题中的异同。

4. (10分)用下列势函数

   $K(x,x_k)=e^{-|x-x_k{|}^2}$

   求解以下模式的分类问题
   $\omega_1\colon{(0,1)^{T,\quad(0,-1)}T}\$

   ${\omega }_2:\{(1,0{)}^T,(-1,0{)}^T\}$

5. (10 分)试述 K-L 变换的基本原理，并将如下两类样本集的特征维数降到一维，同时画出样本在该空间中的位置。
   ${\omega }_1:\{(-5-5{)}^T,(-5-4{)}^T,(-4-5{)}^T,(-5-6{)}^T,(-6-5{)}^T\}$

${\omega }_z:\{(55{)}^T,(56{)}^T,(65{)}^T,(54{)}^T,(45{)}^T\}$,
其中假设其先验概率相等，即 $P({\omega }_1)=P({\omega }_2)=0.5$。

6. (10 分)详细描述AdaBoost算法，解释为什么AdaBoost经常可以在训练误差为0后继续训练还可能带来测试误差的继续下降。

7. (10 分)描述感知机(Perceptron)模型，并给出其权值学习算法。在此基础上， 以仅有一个隐含层的三层神经网络为例，形式化描述 Back-Propagation(BP)算法中是如何对隐层神经元与输出层神经元之同的连接权值进行调整的。

8. (12分)已知正例点$x_1=(3,3{)}^T,x_2=(4,3{)}^T$。负例点$x_3=(1,1{)}^T$,试用线性支持向最机的对偶算法求最大间隔分离超平面和分类决策函数，并在图中画自分离超平面、 间隔边界及支持向量。

9. (12 分)假定对一类特定人群选行某种疾病检在。正常人以 $w_1$类代表，患病者以$w_2$类代表。设被检查的人中正常者和患病者的先验概率分别为
   正常人；$P({\omega }_1)=0.9$
   德瑞者：$P({\omega }_t)=0.1$,
   现有一被检查者，其观察值为x。从类条件概率密度分布曲线上查得
   $P(x|{\omega }_t)=0.2，P(x|{\omega }_t)=0.4$
   同时已知风险损失函数为

   $$\left(\begin{array}{cc}{\lambda }_{11}& {\lambda }_{12}\\ {\lambda }_{21}& {\lambda }_{22}\end{array}\right)=\left(\begin{array}{cc}0& 6\\ 1& 0\end{array}\right)$$​

   其中${\lambda }_{ij}$表示将本应属于第 j 类的模式判为属于第 i 类所带来的风险损失。试对该被检查者用以下两种方法进行分类：
   (1) 基于最小错误率的贝叶斯决策，并写出其判别函数和决策面方程；
   (2) 基于最小风险的贝叶斯决策，并写出其判别函数和决策面方程。

10. (12分)假设有 3 个盒子，每个盒子里都装有红、白两种颜色的球。按照下面的方法抽球，产生一个球的颜色的观测序列：开始，以概率π随机选取 1 个盒子，从这个盒子里以概率 B随机抽出 1 个球，记录其颜色后，放回；然后，从当前盒子以概率 A 随机转移到下一个盒子，再从这个盒子里以概率 B 随机抽出一个球，记录其颜色，放回；如此重复进行 3 次，得到一个球的颜色观测序列$: O= ( 红，白，红) $。请计算生成该序列的概率$P(O|{A,B,\pi})$。

    提示：假设状态集合是{盒子1，盒子2，盒子3},观测的集合是{红，白},本题中已知状态转移概率分布、观测概率分布和初始概率分布分别为：

    A状态转移概率分布	盒子1	盒子2	盒子3
    盒子1	0.5	0.2	0.3
    盒子2	0.3	0.5	0.2
    盒子3	0.2	0.3	0.5

    B观测概率分布	红	白
    盒子1	0.5	0.5
    盒子2	0.4	0.6
    盒子3	0.7	0.3

    初始概率分布$\pi =[0.2,0.4,0.4{]}^T$

2016

1. (6 分)简述模式的概念和它的直观特性,并简要说明模式分类有哪几种主要方法。

2. (8分)假设某研究者在ImageNet数据上使用线性支持向量机(Linear SVM)来做文本分类的任务，请说明在如下情况下分别如何操作才能得到更好的结果，并说明原因.
   (1)训练误差5%,验证误差10%,测试误差10%。
   (2)训练误差1%,验证误差10%,测试误差10%。
   (3)训练误差1%,验证误差3%,测试误差10%。

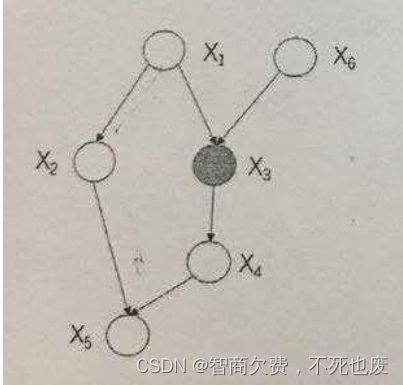
3. 给定如下图所示的概率图模型，其中变量$X_3$为已观测变量，请问变量$X_4$和$X_6$是否独立？并用概率推导证明。

4. (10分)(1)随机猜测作为一个分类算法是否一定比 SVM 差? 借此阐述你对"No Free Lunch Theorem"的理解
   （2）举例阐述你对“Occam`s razor”的理解

5. (10 分)详细描述AdaBoost算法，解释为什么AdaBoost经常可以在训练误差为0后继续训练还可能带来测试误差的继续下降。

6. (10 分)用感知器算法求下列模式分类的解向量(取w(1)为零向量)
   ${\omega }_1:\{(0,0,0{)}^T,(1,0,0{)}^r,(1,0,1{)}^T,(1,1,0{)}^T\}$
   ${\omega }_x:\{(0,0,1{)}^T,(0,1,1{)}^T,(0,1,0{)}^T,(1,1,1{)}^T\}$

7. (12分) 设以下模式类别具有正态概率密度函数：
   ${\omega }_1:\{(0,0,0{)}^T,(1,0,0{)}^T,(1,0,1{)}^T,(1,1,0{)}^T\}$

   ${\omega }_2:\{(0,1,0{)}^T,(0,1,1{)}^T,(0,0,1{)}^T,(1,1,1{)}^T\}$
   若$P({\omega }_1)=P({\omega }_2)=0$.5, 求这两类模式之间的贝叶斯判别界面的方程式。

8. (12分)假设有如下线性回归问题，
   ${\min }_{\beta }(y-X\beta {)}^2+\lambda ||\beta |{|}_2^2$

   其中y和β是n维向量，X是一个m × n的矩阵。该线性回归问题的参数估计可看作一个后验分布的均值，其先验为高斯分布$\beta \sim N(0,\tau I)$, 样本产生自高斯分布$y\sim N(X\beta ,{\sigma }^{2}I)$,其中$I$为单位矩阵，试推导调控系数$\lambda$与方差$\tau$和${\sigma }^2$的关系。

9. (12 分) 给定有标记样本集$D_t=\{(x_1,y_1),(x_2,y_2),...,(x_l,y_l)\}$和未标记样本$D_a=\{(x_{l+1},y_{l+1}),(x_{l+2},y_{l+2}),...,(x_{l+u},y_{l+u})\},l\ll u,l+u=m$, 假设所有样本独立同分布，且都是由同一个包含N 个混合成分的高斯混合模型$\{(a_i,{\mu }_i,{\Sigma }_i)|1\le i\le N\}$产生，每个高斯混合成分对应一个类别，请写出极大似然估计的目标函数(对数似然函数), 以及用 EM 算法求解参数的迭代更新式。

10. (12 分)假定对一类特定人群选行某种疾病检在。正常人以 $w_1$类代表，患病者以$w_2$类代表。设被检查的人中正常者和患病者的先验概率分别为
    正常人；$P({\omega }_1)=0.9$
    德瑞者：$P({\omega }_t)=0.1$,
    现有一被检查者，其观察值为x。从类条件概率密度分布曲线上查得
    $P(x|{\omega }_t)=0.2，P(x|{\omega }_t)=0.4$
    同时已知风险损失函数为

    $$\left(\begin{array}{cc}{\lambda }_{11}& {\lambda }_{12}\\ {\lambda }_{21}& {\lambda }_{22}\end{array}\right)=\left(\begin{array}{cc}0& 6\\ 1& 0\end{array}\right)$$​

    其中${\lambda }_{ij}$表示将本应属于第 j 类的模式判为属于第 i 类所带来的风险损失。试对该被检查者用以下两种方法进行分类：
    (1) 基于最小错误率的贝叶斯决策，并写出其判别函数和决策面方程；
    (2) 基于最小风险的贝叶斯决策，并写出其判别函数和决策面方程。

2017

1. （8）试描述线性判别函数的基本概念，并说明既然有线性判别函，为什么还需要非线性判别函数？假设有两种模式，每类包括6个4维不同的模式，且良好分布。如果他们是线性可分的。问权向量至少需要几个系数分量？假如要建立额尔茨的多项式判别函数，又至少需要几个系数分量？（设模式的良好分布不因模式变化而改变）

2. (8 分)简述SVM算法的原理，如果使用SVM做二分类问题得到如下结果，分别应该采取什么措施以取得更好的结果？并说明原因。
   (I)训练集的分类准确率 90%。验证集的分类准确率 90%, 测试集的分类准确率 88%;
   (2)训练集的分类准确率 98%,验证集的分类准确率 90%,测试集的分类准确率 88%。

3. (8分)请从两种角度解释主成分分析(PCA)的优化目标。

4. (8 分) 请给出卷积神经网络 CNN 中卷积、Pooling、ReLU 等基本层操作的含义。然后从提取特征的角度分析 CNN 与传统特征提取方法 (例如 Gabor 小波滤波器) 的异同。

5. (10分)用线性判别函数的感知器赏罚训练算法求下列模式分类的解向量，并给出相应的判别函数。
   $\omega_1\colon{(0,0)^T,\quad(0,1)T}\$

   ${\omega }_2:\{(1,0{)}^T,(1,1{)}^T\}$

6. (10 分)试述 K-L 变换的基本原理，并将如下两类样本集的特征维数降到一维，同时画出样本在该空间中的位置。
   ${\omega }_1:\{(-5-5{)}^T,(-5-4{)}^T,(-4-5{)}^T,(-5-6{)}^T,(-6-5{)}^T\}$

   ${\omega }_z:\{(55{)}^T,(56{)}^T,(65{)}^T,(54{)}^T,(45{)}^T\}$,
   其中假设其先验概率相等，即 $P({\omega }_1)=P({\omega }_2)=0.5$。

7. (12分)请解释 AdaBoost 的基本思想和工作原理,写出 AdaBoost 算法。

8. (12 分) 选择埃尔米特多项式，其前面几项的表达式
   $H_1\left(x\right)-1,H_2\left(x\right)=2x,H_3\left(x\right)=4x^2-2$
   $H_4(x)=-8x^2-1/2x,H_5(x)=16x^2-48x^2+12$
   试用二次埃尔米特多项式的势函数算法求解以下模式的分类问题
   ${\omega }_1:\{(0,1{)}^T,(0,-1{)}^T]\}$
   ${\omega }_1:\{(1,0{)}^T,(-1,0{)}^T\}$

9. (12分)已知以下关于垃圾部件的8条标注数据。A、B为邮件的2个特征，Y为类别。其中Y=1表示该邮件为垃圾邮件，Y=0 表示该邮件为正常邮件。请依此训练一个朴素贝叶斯分类器。并预测特征为“A=O, B=1”的邮件是否为垃圾邮件。

序号	1	2	3	4	5	6	7	8
A	0	0	1	1	1	1	1	1
B	0	0	0	0	0	0	1	1
Y	1	0	0	0	1	0	0	1

10. (12分)假设有 3 个盒子，每个盒子里都装有红、白两种颜色的球。按照下面的方法抽球，产生一个球的颜色的观测序列：开始，以概率π随机选取 1 个盒子，从这个盒子里以概率 B随机抽出 1 个球，记录其颜色后，放回；然后，从当前盒子以概率 A 随机转移到下一个盒子，再从这个盒子里以概率 B 随机抽出一个球，记录其颜色，放回；如此重复进行 3 次，得到一个球的颜色观测序列$: O= ( 红，白，红) $。请计算生成该序列的概率$P(O|{A,B,\pi})$。

​ 提示：假设状态集合是{盒子1，盒子2，盒子3},观测的集合是{红，白},本题中已知状态转移概率分布、观测概率分布和初始概率分布分别为：

A状态转移概率分布	盒子1	盒子2	盒子3
盒子1	0.5	0.2	0.3
盒子2	0.3	0.5	0.2
盒子3	0.2	0.3	0.5

B观测概率分布	红	白
盒子1	0.5	0.5
盒子2	0.4	0.6
盒子3	0.7	0.3

初始概率分布$\pi =[0.2,0.4,0.4{]}^T$

2018

1. （10分）简述Fisher线性判别方法的基本思路，写出准则函数和对应的解。

2. (12分)的设集个地区细胞识别中正常( $w_1$ )和导常( $w_2$ )两类的先验概率分别为：正常状态：$P(w_1)=0.95$, 异常状态 $P(w_2)=0.05$。现有一待识别的细胞，其观察值为x，已知 $p(x|w_1)=0.2$, $p(x|w_2)=0.5$。同

   $$\left(\begin{array}{cc}{\lambda }_{11}& {\lambda }_{12}\\ {\lambda }_{21}& {\lambda }_{22}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 8& 0\end{array}\right)$$

   其中${\lambda }_{ij}$表示将本应属于第 $j$类的模式判为属于第 $i$ 类所带来的风险损失。试对该待识别细胞用以下两种方法进行分类；

   1. 基于最小错误率的贝叶斯决策。并写的其判别函数和决策面方程。
   2. 基于最小风险的贝叶斯决策，并写出其判别函数和决策面方程。

3. (10分)SVM可以借助核函数(kernel function)在特征空间(feature space)学习一个具有最大间隔的超平面。对于两类的分类问题，任意输入$x$的分类结果取决于下式：
   $$<w,\varphi (x)>+w_0=f(x;\alpha ,w_0)$$
   其中，$\hat{w}$和${\omega }_0$是分类超平面的参数，$\alpha =\{{\alpha }_1,...{\alpha }_{[SV]}\}$表示支持向量(support vector)的系数，SV表示支持向星集合。使用径向基面数(radial basis function)定义核函数$K(\cdot ;)$,即$K(x,x^{\prime })=\exp (-\frac{D(x,x^{\prime })}{2s^2})$。假设训练数据在特征空间线性可分，SVM 可以完全正确地划分这些训练数据。给定一个测试样本$x_{far}$,它距离所有训练样本都非常远。
   试写出$f(x;\alpha ,{\hat{w}}_0)$在核特征空间的表达形式，进而证明$:f(x_{far};\alpha ,{\hat{w}}_0)\approx {\hat{w}}_0$

4. (10 分) K-L变换属于有监督学习 (supervised learning)还是无监督学习(unsupervised learning)? 试利用K-L 变换将以下样本集的特征维数降到一维，同时画出样本在该空间的位置。

   $\{(-5-5{)}^T,(-5-4{)}^T,(-4-5{)}^T,(-5-6{)}^T,(-6-5{)}^T,(55{)}^T,(56{)}^T,(65{)}^T,(54{)}^T,(45{)}^T\}$

5. (12分) 过拟合与欠拟合。

   1. 什么是过拟合？什么是欠拟合？
   2. 如何判断一个模型处在过拟合状态还是欠拟合状态？
   3. 请给出 3 种减轻模型过拟合的方法。

6. (12 分)用逻辑回归模型(logistic regression model)解决$\kappa$类分类问题，假设每个输入样本$x\in {\mathbb{R}}^d$​的后验概率可以表示为：

   $P(Y=k|X=x)=\frac{\exp (w_k^{T}x)}{1+{\sum }_{l=1}^{K-1}\exp (w_l^{T}x)},k=1,...,K-1$

   $P(Y=K|X=x)=\frac{1}{1+{\sum }_{l=1}^{K-1}\exp (w_l^{T}x)}$

   其中$w_k^T$表示向量$w_k$的转置。通过引入$w_K=0$, 上式也可以合并为一个表达式。

   1. 该模型的参数是什么？数量有多少？

   2. 给定 $n$ 个训练样本$\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$ 请写出对数似然函数(log likelihood function) $L$的表达形式，并尽量化简。

   $L(w_1,...,w_{K-1})={\sum }_{i=1}^n\ln P(Y=y_i|X=x_i)$

   3. 如果加入正则化项(regularization term), 定义新的目标函数为：

      $J(w_1,\dots ,w_{K-1})=L(w_1,\dots ,w_{K-1})-\frac{\lambda }{2}{\sum }_{l=1}^K\Vert w_l{\Vert }_2^2$

      请计算$J$ 相对于每个$w_{\mathrm{k}}$的梯度。

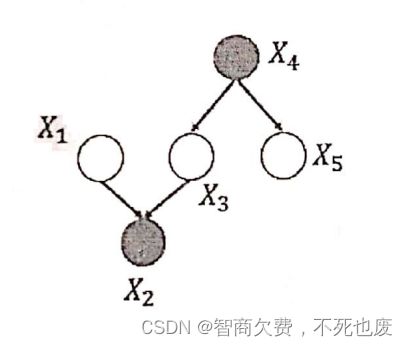
7. 给定如下图所示的概率图模型，其中变量$X_2、X_4$为已观测变量，请问变量$X_1$和$X_5$是否独立？并用概率推导证明。

9. (12分)假设有2校硬币，分别记为A和B，以π的概率选择A，以1-π的概率选择B，这些硬币正面出现的概率分别是$p$和$q$。掷选出的硬币，记正面出现为1，反面出现为0，独立地重复进行 4次试验，观测结果如下：1,1,0,1。给定模型参数$\pi =0.4,p=0.6,q=0.5$,请计算生成该序列的概率，并给出该观测结果的最优状态序列。

10. 基于AdaBoost算法的目标检测需要稠密的扫描窗口并判断每个窗口是否为目标，请描述基于深度学习的目标检测方法，如SSD或YOLO，如何做到不需要稠密扫描窗口而能发现并定位目标位置

2019

一、(16分)选择题。

1. 基于二次准则函数的H-K 算法较之于感知器算法的优点是哪个？

   A.计算量小 \quad B.可以判别问题是否线性可分 \quad C.其解完全适用于非线性可分的情况

2. 在逻辑回归中，如果正则项取$L_1$正则，会产生什么效果？
   A.可以做特征选择，一定程度上防止过拟合 \quad B.能加快计算速度 \quad C.在训练数据上获得更准确的结果

3. 如果模型的偏差较高，我们如何降低偏差？
   A.在特征空间中减少特征 \quad B、在特征空间中增加特征 \quad C.增加数据点

4. 假设采用正态分布模式的贝叶斯分类器完成一两个分类任务，则下列说法正确的是哪个

   A.假设两类的协方差矩阵均为对角矩阵，则判别界面为超平面。
   B.假设两类的协方差矩阵相等，则判别界面为超平面。
   C.不管两类的协方差矩阵为何种形式，判别界面均为超平面。

5. 下列方法中，哪种方法不能用于选择 PCA 降维 (K-L 变换) 中主成分的数目$K$?
   A.训练集上残差平方和随$K$发生剧烈变化的地方(肘部法)

   B.通过监督学习中验证集上的性能选择K
   C.训练集上残差平方和最小的K

6. 考虑某个具体问题时，你可能只有少量数据来解决这个问题。不过幸运的是你有一个针对类似问题已经预先训练好的神经网络，请问可以用下面哪种方法来利用这个预先训练好的网络
   A. 把除了最后一层外所有的层都冻住，重新训练最后一层
   B.对新数据重新训练整个模型
   C, 只对最后几层进行调参(fine tune)

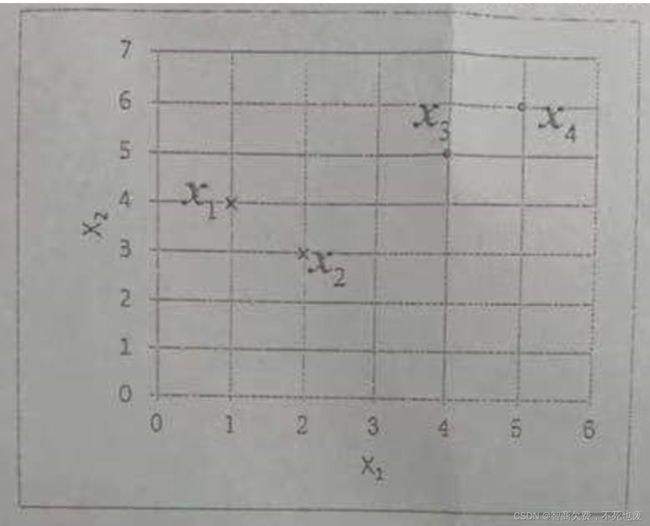
7. 如下图所示，假设该数据集中包含一些线性可分的数据点。训练 Soft margin SVM 分类器，其松弛项的系数 为C。请问当$C\to 0$时，分类边界为下图中的哪个？

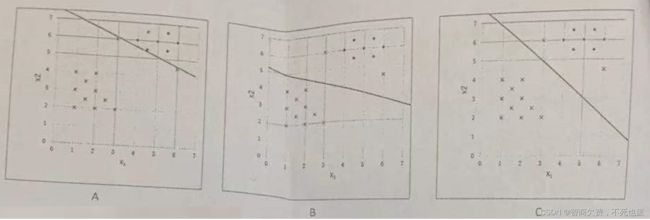
8. 如下图所示。假设该数据集中包含线性不可分的数据点。采用二次核函数训练 Soft margin SVM 分类器，请问当$C\to \infty$时，份类边界为下图中的哪个？外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

二、(6分) 请列举半监督学习对数据样本的三种基本假设。

三、(8分)针对下图所示的三种数据分布。从K均值、GMM 和 DBSCAN 中分别选择最合适的聚类算法、并简述理由。外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

四、(12 分)对于具有类别标签的数据、采用K-L变换和 Fisher 线性判别分析两种方法对数据降维。

(1)简选这两种数据毕维方法的基本过程。(8分)
(2) 这两种方法中哪种方法对分类夏有效？并简述原因。(4分)

五、(10 分) 逻辑回妇

(1)简达逻辑回归算法的原理。(4分)
(2)如果使用逻辑回归算法做二分类问题得到如下结果，分别应该采取什么措施以取得更好的结果？并说明理由(6分)

​ (a)训练集的分类准确率85%，验证集的分类准确率 80%，测试集的分类准确率75%；
​ (b)训练集的分类准确率 99%，验证集的分类准确率 80%，测试集的分类准确率 78%;

六、(10分)解释 AdaBoost算法的基本思想和工作原理、并给出 AdaBoost 算法的伪代码。

七、(10 分))从特征提取的角度，分析深度卷积神经网络与传统特征提取方法(例如 Gabor 小波滤波器)的异同，并给出深度学习优于传统方法的原因。

八、(8分)硬间隔支持向量机(Hard margin SVM)

如下图所示，一个数据集包含来自2个类别的4个数据点。在此集合上训练一个线性 Hard margin SVM 分类器。请写出SVM 的形式化模型，并计算出该分类器的权重向量$w$和偏差b、给出该分类器的支持向量

九、(16 分)拟利用贝叶斯判别方法检测 SNS 社区中不莫实账号。设$Y=0$表示真实账号。$Y=1$表示不真实账号。每个用户有三个属性，$X_1$表示日志数量/注册天数，$X_2$表示好友数量/注册天数，$X_3$衰示是否使用真实头像。已知$P(Y=0)=0.89,P(X_3=0|Y=0)=0.2,P(X_3=0|Y=1)=0.9$。且给定$Y$的情况下$X_1\times X_2$的分布如下：

$P(X_1|Y)$	$X_1\le 0.05$	$0.05\le X_1\le 0.2$	$X_1\ge 0.2$
$Y=1$	0.8	0.1	0.1
$Y=0$	0.3	0.5	0.2

$P(X_2|Y)$	$X_2\le 0.1$	$0.1\le X_2\le 0.8$	$X_2\ge 0.8$
$Y=1$	0.7	0.2	0.1
$Y=0$	0.1	0.7	0.2

若一个账号使用非真实头像，日志数量与注册天数的比率为0.1,好友数与注册天数的比率为0.2, 判断该账号是不是虚假账号。

十、(10分)现装有红色球和白色球的两个盒子，盒子 1 中红球的比例为p，盒子 2 中红球的比例为$q$。我们以概率π选择盒子1，概率$1-\pi$选择盒子 2,然后从盒子中有放回地取出一个小球，独立地重复进行 4 次试验，观测结果为：红，红，白，红。

假定模型的参数初始值为${\pi }^{(0)}=0.4,p^{(0)}=0.4,q^{(0)}=0.5$,请写出 EM算法迭代一次后p和$q$的值。(计算结果保留两位小数)

2021

一、(20分)选择题。

1. 对于两类分类问题，()能发现类别不可分的情况。
   A.梯度法 \quad B.H-K 算法 \quad C.感知器算法

2. 下列机器学习模型不属于生成式模型的是()。
   A.朴素贝叶斯 \quad B. 隐马尔科夫模型 (HMM) \quad C. Logistic Regression (逻辑回归) 模型

3. 下列方法中，不属于无监督特征降维的方法是 ()。
   A.主成分分析(PCA) \quad B.线性判别分析(LDA) \quad C. 自编码器

4. 如果模型的偏差很高，我们如何降低模型偏差？()
   ​ A、在特征空间中减少特征 \quad B.在特征空间中增加特征 \quad C. 增加训练数据的数量

5. 对一个分类任务，我们采用梯度下降法训练得到一个 20 层的深度卷积神经网络模型。你发现它在训练集上的正确率为 98%,但在验证集上的正确率为 70%。以下哪项操作有可能提高模型在测试集上的性能？()
   A. 增加正则项的权重 \quad B. 减少训练样本的数量 \quad C.加大模型的训练次数

6. 要将下图所示的两个半月形数据各聚成两簇，可采用()聚类算法。

   

   A. K均值聚类 \quad B.混合高斯模型(GMM) \quad C.DBSCAN

7. 下列哪一项不是半监督学习的假设？()

   A.低密度分离假设 \quad B.流形假设 \quad C.最小描述长度假设

8. 给定如下图所示的概率图模型，请问下列哪一项正确?

   

   A. $X_1\perp X_4$ \quad \quad B. $X_1\perp X_5|\{X_3,X_4\}$ \quad \quad C. $X_1\perp X_3|X_2$

9. 虽然神经网络在上世纪 80 年代就已被提出，但直到近些年才能成功训练深度模型，原因之一是现代深度神经网络采用了()技术。

   A.反向传播算法 \quad B.Sigmoid激活函数 \quad C. 跳跃连接(skip connect)

10. 下列哪一项技术使得卷积神经网络具有非线性建模能力？()
    A.随机梯度下降优化算法 \quad B.ReLU激活函数 \quad C.卷积

二、(12 分)给定$N$ 个独立分布训练数据$\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中$x_i\in R^D,y_i\in \{0,1\}$为类别标签，当$y_i=1$时，表示$x_i$为异常数据；$y_i=0$时，表示$x_i$为正常数据。

（1）请用贝叶斯分类器来构造判别函数，并阐述如何估计相关的参数（假设每类样本的特征服从多元高斯分布）

（2）如果将正常的数据误分为异常的代价为1，将异常误分为正常的代价为5，请阐述如何构建分类器或判别函数。

三、给定一个有N个样本组成的训练集$\{x_i{\}}_{i=1}^N$，其中$x_i\in R^D$，请形式化描述如何构建主成分分析（PCA）模型，以及如何对新的测试样本$x\in R^D$进行降维和重构。

四、(8 分) 对于二分类问题，Logistic Kegression(逻辑回归) 中利用下式计算后验概率。

$P(y=1|x)=\frac{1}{1+\exp (-w^{\mathrm{T}}x)}$
给定训练数据$\{(x_i,y_i){\}}_{i=1}^N,y_i\in \{0,1\}$,请给出求解模型参数w的方法

五、(8分) 给定如下训练数据集：

$x_1=\left(\genfrac{}{}{0ex}{}{4}{4}\right),x_2=\left(\genfrac{}{}{0ex}{}{5}{4}\right),x_3=\left(\genfrac{}{}{0ex}{}{2}{2}\right),y_1=1,y_2=1,y_3=-1,$
通过求解SVM的对偶问题来求解最大间隔的分离超平面。

六、(10分)请写出两种非线性降维方法，并分别简述其思想原理。

七、(10分) 请给出装装（Bagging）算法和提升（Boosting）算法的至少 3 个不同点。

八、(12 分)假设有 3 个盒子，每个盒子里装有不同数量的红、蓝两种颜色的小球： 盒子1：2个红球，2个蓝球：

盒子2：3个红球，1个蓝球；
盒子3：1个红珠，3个蓝球。
每次随机选择一个盒子，并从中抽取一个球(有放回)。
(1) 请用隐马尔可夫模型(HMM)描述上述过程，并给出参数$\pi ,A,B$的值：(4分)
(2) 在实验过程中我们只记录了抽取到的球的颜色，忘了记录盒子的标号。假如观测到小球的颜色序列为$O=(红，蓝)$，请用维特比(Viterbi)算法计算最可能的盒子序列。(8 分)

九、(10 分) 用于图像分类等任务的卷积神经网络是如何解决从像素级低层语义到物体类别级高层语义之间“语义鸿沟”门题的？