C程序训练:蛇形矩阵
题目描述:用数字1,2,3,4,...,n*n这n^2个数蛇形填充规模为n*n的方阵。蛇形填充方法为:
对于每一条左下-右上的斜线,从左上到右下依次编号0,1,...,2n-2;按编号从小到大的顺序,将数字从小到大填入各条斜线,其中编号为奇数的从左下向右上填写,编号为偶数的从右上到左下填写。
比如n=4时,方阵填充为如下形式:
1 3 4 10 2 5 9 11 6 8 12 15 7 13 14 16
输入格式:只有1行,为一个整数n,代表蛇形的阶数,n的范围是1-15。
输出格式:共n行,为蛇形矩阵。每行的每个元素使用格式符"%5d"输出。每行最后一个数的后面为换行符。
输入样例:
5
输出样例:
1 3 4 10 11
2 5 9 12 19
6 8 13 18 20
7 14 17 21 24
15 16 22 23 25
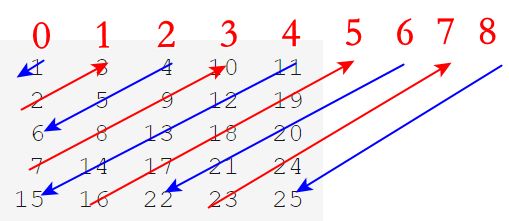
方法1:按题意写程序。如图1所示,对于5*5的矩阵而言,有2*5-1=9条斜线,我们把斜线分为上半部和下半部来写,上半部从1到5共5条斜线,下半部从6到9共4条斜线。上半部每条斜线的数字个数是递增,下半部每条斜线数字个数是递减。编号为奇数的从左下向右上填写,其行编号递增,列编号递减;编号为偶数的从右上到左下填写,其行变换递减,列编号递增,按此思路编写程序即可。
图1 5*5矩阵
源程序如下:
#include
int main()
{
int n,a[100][100],i,j,s=1;
scanf("%d",&n);
// 处理上半部
for(i=0; i 优化: 仔细观察矩阵,发现矩形存在一种对称关系。观察图1的5*5矩阵,我们发现a[0][0]=1, a[4][4]=n*n=25;a[0][1]=3; a[4][3]=23; a[1][0]=2, a[3][4]=24; ……
a[0][0]+a[4][4]=n*n+1=26;
a[0][1]+a[4][3]=26;
a[1][0]+a[3][4]=26;
……
该矩阵存在对称性,对称轴为矩阵的副对角线,因此只需要遍历一半副对角线左边或者右边的元素就行了。利用这个特点,优化后的程序如下:
#include
int main()
{
int n,a[100][100],i,j,s=1;
scanf("%d",&n);
// 处理上半部
for(i=0; i 方法2:按蛇形走位如图2所示。分下行(从右上角到左下角走)和上行(从左下角到右上角),先从左上角斜线开始填写。
图2 5*5矩阵
若下标超出对角线上角时,转移到下一行的最后一列;若超出对角线下角时,转移到最后一行第一列。
若下标超过最后一列,则转移到下一行最后一列。若下标超过第一列,则转移到 下一行第一列。
若下标超过最后一行,则转移到最后一行下一列。若下标超过第一行,则转移到第一行的下一列。
按此算法编写程序如下:
#include
int main()
{
int n,a[100][100],i,j;
int x=1, m=1;
scanf("%d",&n);
for(i=0,j=0; x <= n*n;){
if(m==1){ // 下行
a[i++][j--] = x++;
if(i>n-1 && j<0) m=-m,--i,j=1; // 超出下对角线
else if (i>n-1) m=-m,--i,j+=2; // 超出最后一行
else if (j<0) m=-m,j=0; // 超出第1列
}else { // 上行
a[i--][j++] = x++;
if(i<0 && j>n-1) m=-m, i=1, --j; // 超出上对角线
else if (i<0) m=-m,i=0; // 超出第1行
else if (j>n-1) m=-m, --j, i+=2; // 超出最后一列
}
}
// 输出
for(i=0; i 按方法1中的优化方法进一步优化后的程序如下。
#include
int main()
{
int n,a[100][100],i,j;
int x=1, m=1;
scanf("%d",&n);
int num = n*(n+1)/2;
for(i=0,j=0; x <= num;){
if(m==1){ // 下行
a[i++][j--] = x++;
if(i>n-1 && j<0) m=-m,--i,j=1; // 超出下对角线
else if (i>n-1) m=-m,--i,j+=2; // 超出最后一行
else if (j<0) m=-m,j=0; // 超出第1列
}else { // 上行
a[i--][j++] = x++;
if(i<0 && j>n-1) m=-m, i=1, --j; // 超出上对角线
else if (i<0) m=-m,i=0; // 超出第1行
else if (j>n-1) m=-m, --j, i+=2; // 超出最后一列
}
}
// 处理下半部
int step = n*n + 1;
for(i=1; i 该程序看起来仍然很复杂,进一步优化,程序如下。
#include
int main()
{
int a[100][100],s=1,n;
int i,j, m;
scanf("%d",&n);
// 处理上半部,按蛇形走位
for(m =0; m < n; m += 2) { // 上半部斜线共n条(包括对角线)
for(i=0,j=m; j>=0 && i=0 && j 方法3:方法2的改进版,蛇形走位与对称结合起来实现。
#include
int main()
{
int n, a[100][100];
int sL, sR;
scanf("%d", &n);
sL = 1, sR = n * n;
for (int m = 0; m < n; m++) {
for (int i = 0; i <= m; i++) {
if (m % 2 == 0) { // 下行
a[i][m - i] = sL++;
a[n-1-i][n-1-(m-i)] = sR--; // 对称
} else { // 上行
a[m - i][i] = sL++;
a[n-1-(m-i)][n-1-i] = sR--; // 对称
}
}
}
// 输出
for(int i=0; i 方法4:不使用数组,直接计算数组各元素。
#include
int main()
{
int n;
scanf("%d", &n);
int total = n *2 - 1;
for (int i = 0; i < n; ++i) {
for (int j =0; j< n; ++j){
int line = i + j, x;
if (line < n){
x =(line + 1) * line / 2;
x +=(line & 1 ? j: line - j)+ 1;
} else {
x = n * ( n + 1) / 2;
int k = line - n;
x += (total - k) * k / 2;
k = j - 1 - k;
x += (line & 1 ? k + 1: total - line - k);
}
printf("%5d", x);
}
printf("\n");
}
return 0;
}
参考文献:
[1]李红卫,李秉璋. C程序设计与训练(第四版)[M],大连,大连理工大学出版社,2023.
[2]https://pan.baidu.com/s/17ZXphwqySNIsIgcGtYMjvg?pwd=lhwc