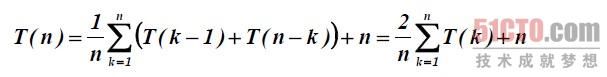12.28大虫——数据结构与算法——选择题专练（部分，完）
复杂度
二分查找，哈希散列表
（1+14）/2=7，mid=7,7不是，所以下一次的右端点是mid-1=6,（1+6）/2=3
3不是，下一次左端点是mid+1=4，(4+6)/2=5,(4+5)/2=4;
即7,3,5,4为C
P要求尽可能大，而且还得是素数
（1+20）/2=10，（11+20）/2=15，注意此时左端点未访问，所以不更新左端点，只是知道中间的节点不是，所以就是更新右端点为Mid-1；（11+14）/2=12，即路径为10，15，12
链表
在单链表中，如果只有一个中间指针，则不能删除节点，即不能任意删除中间节点
D尾指针的单循环
堆
n/2
树
第1层有1个，第二层2个，第三层4个，第N层，最多2^(n-1)
最多1个，最多3个，最多7个，深度为n，最多(2^n)-1，2^6=64,则深度为7，选B
n=n0+n1+n2;入度=出度，除了根节点外，其它每个节点都只有一个入度，所以n-1=n1+2n2
即n0+n1+n2-1=n1+2n2,即n0+1=n2，所以出度为2的节点个数为51，总结点数为131
D，一开始都入队，每次合并两个最小的，合并两个最小，就是保证每次一定减小一个最小的，最后队列中保留一个节点，就是说，原来队列中用N个原始的叶子节点，然后每次出队两个，合成后入队一个，也就是说每次操作都会定量减少一个，初始一共n个，所以会操作N-1次，入队n-1次，也就是构建了n-1个非叶子节点，所以总结点数为2n-1
先序是根左右，后序是左右根，正相反的话，可能为根左，左根，根右，右根，即高度等于其结点数 B
查找的复杂度为logn
图
在图邻接矩阵当中，列数代表终点，行数代表起点，要求入度就是固定终点不动，即固定列下的所有行的和，即第i列
2(n-1),注意是度，所以都练到一个点上，其它所有边
邻接矩阵gij,i是起点，j是终点，所以i的出度是i不变，j变，就表示从i出的边。那么入度就是j不变，i变，就是第j列的所有行数的和。对应这题就是第i列的元素和
排序
A,插入排序，由于已经有序，所以逐渐扩大牌堆，和左侧比较，一共需要n-1次比较
B.选取最右侧为基元，左指针为最左侧，右指针为最右侧-1，然后左指针移动不做限制，要找第一个比基元大的，右指针移动要比当前的大（即目的是找到第一个比基元小的），如果最后交换完后左指针大于等于右指针，那么就退出，最后返回的应该是左指针；如果已经是有序的了，每次都是确定一个最右侧最大的元素，然后从左扫到右，即对于左指针，那么就是n+n-1到1，就是On^2
C.从中间分两半，然后进行比较
选择排序是选出此时未排里的最大或最小，然后放到一端，和插入排序是两种
插入排序是逐渐扩大牌堆，选择排序是逐渐缩小未排的
可以每次都确定一个的是，选择，冒泡，堆排，快排
不能的是归并、插入
归并排序
C,堆排序，冒泡排序，快排每次都能确定一个
C
快排性质
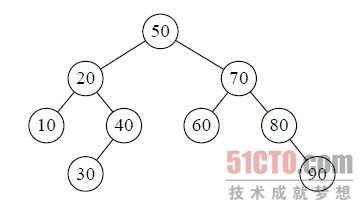
快速排序的时间性能取决于快速排序递归的深度，可以用递归树来描述递归算法的执行情况。如图9‐9‐7所示，它是{50,10,90,30, 70,40,80,60,20}在快速排序过程中的递归过程。由于我们的第一个关键字是50，正好是待排序的序列的中间值，因此递归树是平衡的，此时性能也比较好。
|
|
| 图9-9-7 |
在最优情况下，Partition每次都划分得很均匀，如果排序n个关键字，其递归树的深度就为.log2n.+1（.x.表示不大于x的最大整数），即仅需递归log2n次，需要时间为T（n）的话，第一次Partiation应该是需要对整个数组扫描一遍，做n次比较。然后，获得的枢轴将数组一分为二，那么各自还需要T（n/2）的时间（注意是最好情况，所以平分两半）。于是不断地划分下去，我们就有了下面的不等式推断。
- T（n）≤2T（n/2） +n，T（1）=0
- T（n）≤2（2T（n/4）+n/2） +n=4T（n/4）+2n
- T（n）≤4（2T（n/8）+n/4） +2n=8T（n/8）+3n
- ……
- T（n）≤nT（1）+（log2n）×n= O(nlogn)
也就是说，在最优的情况下，快速排序算法的时间复杂度为O(nlogn)。
在最坏的情况下，待排序的序列为正序或者逆序，每次划分只得到一个比上一次划分少一个记录的子序列，注意另一个为空。如果递归树画出来，它就是一棵斜树。此时需要执行n‐1次递归调用，且第i次划分需要经过n‐i次关键字的比较才能找到第i个记录，也就是枢轴的位置，因此比较次数为
，最终其时间复杂度为O(n2)。
平均的情况，设枢轴的关键字应该在第k的位置（1≤k≤n），那么：
|
|
由数学归纳法可证明，其数量级为O(nlogn)。
就空间复杂度来说，主要是递归造成的栈空间的使用，最好情况，递归树的深度为log2n，其空间复杂度也就为O(logn)，最坏情况，需要进行n‐1递归调用，其空间复杂度为O(n)，平均情况，空间复杂度也为O(logn)。
可惜的是，由于关键字的比较和交换是跳跃进行的，因此，快速排序是一种不稳定的排序方法。