【详解】二叉树的构造及线索化二叉树

目录

二叉树的构造

介绍：

定理1

定理2

例题：

两个定理的运行结构如下：

线索二叉树的定义：

创建的代码：

遍历线索化二叉树

结语：

---

二叉树的构造

介绍：

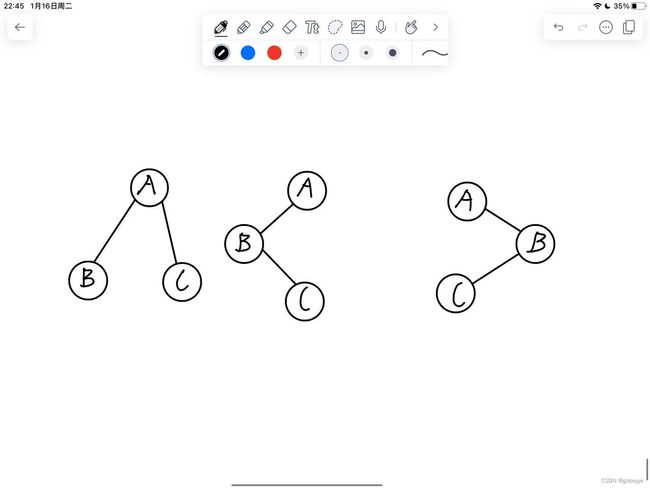
假设二叉树中的每个结点值为单个字符，而且所有结点值均不相同，同一颗二叉树具有唯一的先序序列，中序序列和后序序列，但不同的二叉树可能具有相同的先序序列，中序序列和后序序列。这也说明了当当只看一个序列的化，二叉树没有唯一性。

例如下图，采用先序遍历看的话下面序列都为ABC。

那么这么样才能使二叉树确定下来，毕竟只有这样二叉树的实用价值才会比较高。

到这我们就引出今天要学的两个定理。

定理1：任何n个不同结点的二叉树，都可以由它的中序序列和先序序列唯一地确定。

定理2：任何n个不同结点的二叉树都可由它的中序序列和后序序列唯一确定。

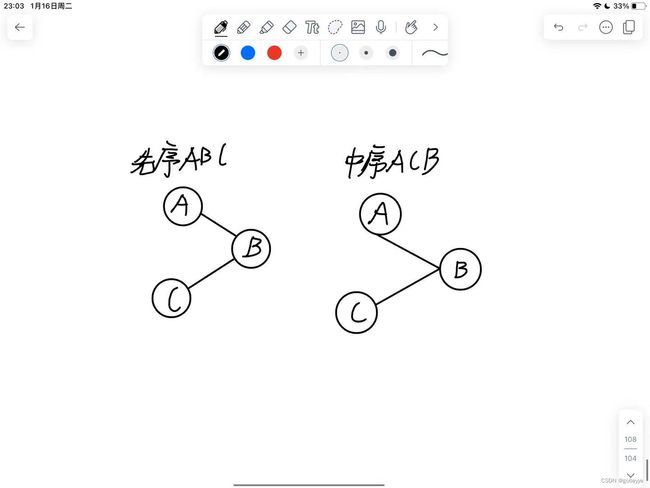
下面就是定理1的一个实际例子，我们可以看到在有先序ABC和中序ACB后，我们二叉树的树形也就确定了下来。

特别注意：只有先序和后序序列是不能确定二叉树的树形。

上面的这两个定理都是采用数学归纳法来证明的。因为这个并不是本文重点，且我们重心也并不在证明这里，故这里我就简单的描述一下，有兴趣的读者可自行证明。例如定理一，是采用在先序序列中找到根节点，在中序序列找到根结点左右的左子树和右子树。和先序序列中的左右子树相对应。特别注意这里相对应是指元素一样，顺序可以不一样，知道左右子树都为空子树是停止循环。

定理1

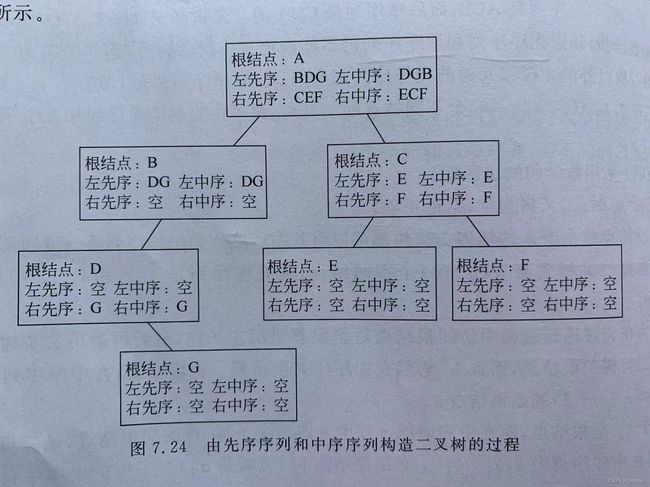
具体过程如下图所示

由上述定理得到以下构造二叉树的算法：

pre存放先序序列，in存放中序序列，n为二叉树的结点个数，本算法执行后返回构造的二叉树的根结点指针b。具体代码如下。

下面的b->lchild = CreateBT1(pre + 1, in, k);，pre+1是为了跳过前面的根节点，in不用变只要控制后面的k即可，因为in不变他还是从初始开始查找，in的左边是左子树正好是我们需要的，故我们只要控制好k，in的遍历是通过k来控制的。

BTNode* CreateBT1(char* pre, char* in, int n)
{
	BTNode* b;
	char* p=NULL;
	if (n <= 0) return NULL;
	b = (BTNode*)malloc(sizeof(BTNode));
	b->data = *pre;
	for (p = in; p < in + n; p++) if (*p == *pre) break;
	int k = p - in;
	b->lchild = CreateBT1(pre + 1, in, k);
	b->rchild = CreateBT1(pre + 1 + k, p + 1, n - k - 1);
	return b;
}

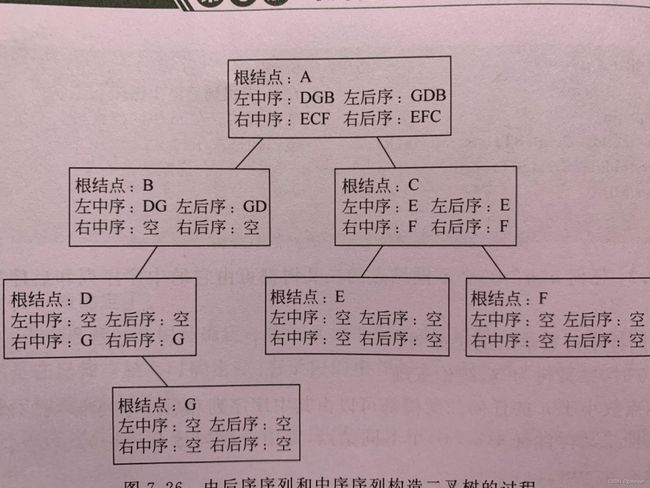
定理2

上述定理的到以下构造二叉树的算法：

post存放后序序列，in存放中序序列，n为二叉树的结点个数，本算法执行后返回构造的二叉链根节点指针b。

b->rchild = CreateBT2(post + k, p + 1, n - k - 1);，post+k是因为后序遍历是先左右子树后根节点，post+k是为了跳过左子树进入右子树，p+1同意如此，遍历in的有子树，n-k-1是右子树的结点数这和前面的先序中序确认二叉树的树形是一样的。

BTNode* CreateBT2(char* post, char* in, int n)
{
	BTNode* b;
	char* p;
	if (n <= 0) return NULL;
	char r = *(post + n - 1);
	b = (BTNode*)malloc(sizeof(BTNode));
	b->data = r;
	for (p = in; p < in + n; p++) if (*p == r) break;
	int k = p - in;
	b->lchild = CreateBT2(post, in, k);
	b->rchild = CreateBT2(post + k, p + 1, n - k - 1);
	return b;
}

为了更好的帮助大家理解这两种创建方法下面我给出一个例题大家可以练练手。

例题：

设计一个算法，将二叉树的顺序存储结构转换成二叉链存储结构。

该题是递归题下面我给出它的模型

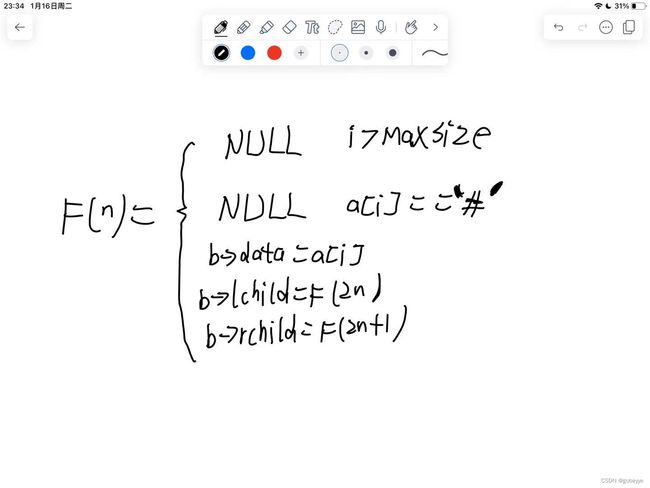
设二叉树的顺序存储结构为a，有f（a，i）返回创建的以a【i】为根结点的二叉链存储结构（初始调用为b = f（a，1））.转换过程对应的递归模型如下：

可能有的朋友不太能明白为什么b->lchild = F(2*n)和b->rchild = F(2*n+1)？这是因为二叉树的性质，如果不太明白的话说明这块知识点不太清楚要回去复习了

性质：若编号为i的结点有左孩子结点，则左孩子结点的编号为2*i；若编号为i的结点有右孩子，则有孩子结点编号为2*i+1.

对应的代码如下：

BTNode* trans(SqBTree a, int i)
{
	if (i > MaxSize) return NULL;
	if (a[i] == '#') return NULL;
	BTNode* b = (BTNode*)malloc(sizeof(BTNode));
	b->data = a[i];
	b->lchild = SqBTree(a, 2 * i);
	b->rchild = SqBTree(a, 2 * i + 1);
	return b;
}

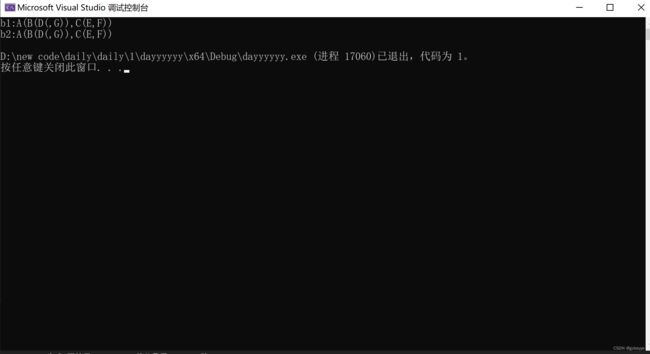
两个定理的运行结构如下：

运行结果如下：

---

线索二叉树的定义：

为什么要有线索二叉树这个东西存在呢？我们可以看到当采用二叉链存储结构是，每个结点有两个指针域，总共有2那个指针域，又由于只有n-1个结点被有效指针所指向，则总共有2n-（n-1）=n+1个空链域。那么我们可以用这些空链域来优化我们的代码，增加了前驱节点和后继结点。并将这些结点称为线索，创建线索的过程称为线索化，线索化的二叉树称为线索二叉树。和前面讲的二叉树的构造一样这样也会因为先序，中序和后序遍历得到不同的线性二叉树，为了叙述简单下面的二叉树均采用中序遍历。

将文字提出得出下图：

由上图我们可以得出相应的二叉树结点声明，为了实现线索化二叉树，将前面二叉树结点的类型声明修改如下：

typedef char ElemType;
//线索化二叉树
typedef struct node
{
	ElemType data;
	int ltag, rtag;
	struct node* lchild;
	struct node* rchild;
}TBTNode;

下面代码实现是通过以下TBTNode* CreateThread(TBTNode* b)和void Thread(TBTNode* p)//对二叉树p进行中序线索化，CreateThread主要是创建一个头结点将树连在一起，有头结点我们对二叉树的各种操作就好做了许多。

Thread算法类似中序遍历，在里面p访问当前结点，pre访问前一个结点。若结点p原来左指针为空，改为指向pre的做线索，若结点pre原来右指针为空，改为指向结点p的右线索。

CreateThread（b）算法的思路是先创建头结点root，将lchild设为链指针，rchild为线索，将root的lchild指向结点b，首先p指向结点b，pre指向头结点root，再调用Thread（b）对整个二叉树进行线索化，最后加入指向头结点的线索，并将头结点的rchild指针线索化为指向最后一个结点（由于线索化直到p等于NULL为止，所以最有访问的是结点pre，和我们前面所学习的链表是一样的。）

创建的代码：

#define  _CRT_SECURE_NO_WARNINGS 1
#include 
#include 
typedef char ElemType;
//线索化二叉树
typedef struct node
{
	ElemType data;
	int ltag, rtag;
	struct node* lchild;
	struct node* rchild;
}TBTNode;
TBTNode* pre;
void Thread(TBTNode* p)//对二叉树p进行中序线索化
{
	if (p != NULL)
	{
		Thread(p->lchild);
		if (p->lchild == NULL)
		{
			p->lchild = pre;
			p->ltag = 1;
		}
		else p->ltag = 0;
		if (pre->rchild == NULL)
		{
			pre->rchild = p;
			pre->rtag = 1;
		}
		else pre->rtag = 0;
		pre = p;
		Thread(p->rchild);
	}
}
TBTNode* CreateThread(TBTNode* b)
{
	TBTNode* root;
	root = (TBTNode*)malloc(sizeof(TBTNode));
	root->ltag = 0; root->rtag = 1;
	root->rchild = b;
	if (b == NULL)
	{
		root->lchild = root;
	}
	else
	{
		root->lchild = b;
		pre = root;
		Thread(b);
		pre->rchild = root;
		pre->rtag = 1;
		root->rchild = pre;
	}
	return root;
}

遍历线索化二叉树

遍历线索化二叉树就是从该次序下的开始结点出发（中序找左子树，先序找根，后序找左子树），反复找到该节点在该次序下的后继结点，直到头结点。

代码如下：

void ThInOrder(TBTNode* tb)
{
	TBTNode* p = tb->lchild;
	while (p != tb)
	{
		while (p->ltag == 0) p = p->lchild;
		printf("%c", p->data);
		while (p->rtag == 1 && p->rchild != tb)
		{
			p = p->rchild;
			printf("%c", p->data);
		}
		p = p->rchild;
	}
}

可以看到该算法是非递归的，尽管其时间复杂度仍然为O（n），但空间性能得到了改善，空间复杂度为O（1）。

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。