【QT+VTK 学习笔记】13:VTK图形处理2 法向量、曲率计算、网格平滑
前言
“VTK图形图像开发进阶_张晓东_罗火灵”的学习笔记。
东灵工作室 教程系列导航:http://blog.csdn.net/www_doling_net/article/details/8763686
学习资料
VTK官网学习地址:https://vtk.org/doc/nightly/html/
2.1法向量计算
法向量的定义
法向量,是空间解析几何的一个概念,垂直于平面的直线所表示的向量为该平面的法向量。法向量适用于解析几何。由于空间内有无数个直线垂直于已知平面,因此一个平面都存在无数个法向量(包括两个单位法向量)。

直线的法向量是与方向向量相垂直的向量。
三维平面的法向量是指垂直于该平面的三维向量。曲面在某点P处的法向量为垂直于该点切平面的向量。对于一个网格模型,其每一个点和单元都可以计算一个法向量,在三维计 算机图形学中法向量一个重要的应用是光照和阴影计算。对于网格模型,模型是由一定数量的面片(单元)来逼近的,面片越多,则模型越精细;反之,则越粗糙。
vtkPolyDataNormals
VTK中计算法向量的Filter为vtkPolyDataNormals该类针对单元为三角形或者多边形 类型的vtkPolyData数据进行计算。
由于法向量分为点法向量和单元法向量,
可以通过函数 SetComputeCellNormals()和SetComputePointNormals()
来设置需要计算的法向量类型。默认情 况下计算点法向量,关闭单元法向量计算。
2.2符号化 Glyphing
模型的法向量数据是向量数据,因此法向量不能像前面讲到的通过颜色映射来显示。但是可以通过符号化(Glyphing)技术将法向量图形化显示如下图右边的面具效果。
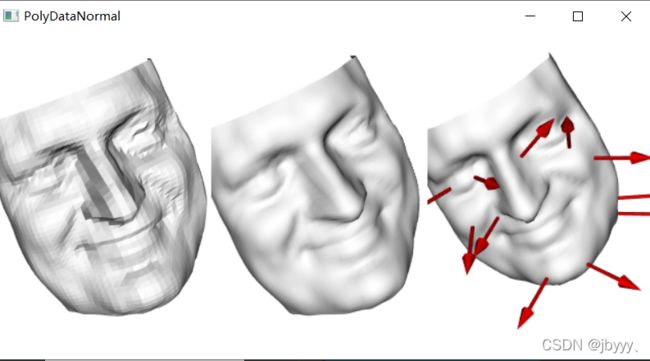
计算法向量前后的模型显示效果图。从图中可以看出,加入法向量后,模型显 示得更加平滑,而未计算法向量的模型看起来比较粗糙。
#include 2.3曲率计算
VTK中的vtkCurvatures类实现了四种计算网格模型点曲率的计算方法。该类接受一个 vtkPolyData数据,将计算得到的曲率数据作为网格模型的点的属性数据存入返回的 vtkPolyData中。
实例:一个网格模型的曲率计算,并通过颜色映 射表来显示模型表面的曲率
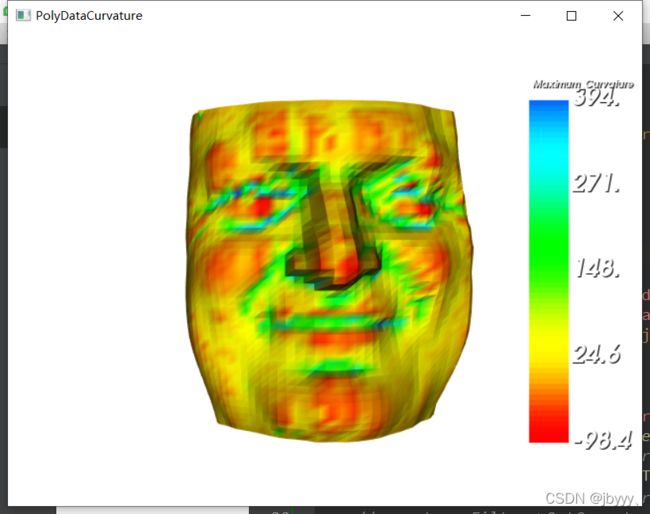
#include 网格平滑
现代扫描技术的发展使得获取点云数据不再困难,通过曲线重建技术可以获取表面网格来表示各种复杂的实体。但是点云数据中往往存在噪声,这样得到的重建网格通常都需要进行平滑处理。
拉普拉斯平滑是一种常用的网格平滑算法。该方法的原理比较简单,如下图所示:
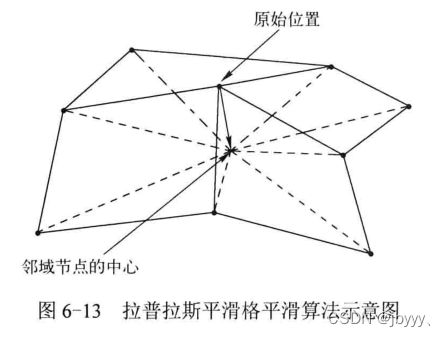
将每个点用其邻域点的中心来代替。通过不断地迭代,可以得到较为光滑的网格。
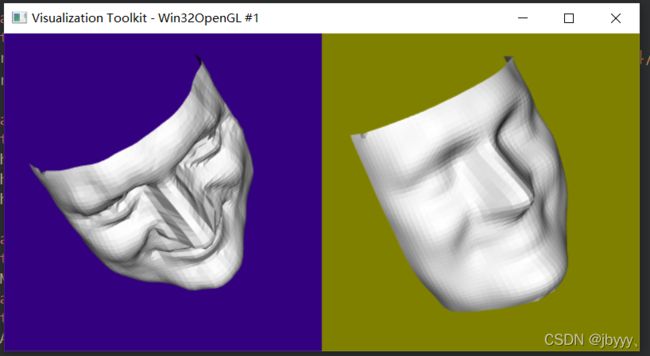
VTKSmoothPolyDataFilter类实现了网格的拉普拉斯平滑算法,使用方法如下:
参考:https://blog.csdn.net/weixin_38293453/article/details/104689138
#include wndSincSmoothFilter =
// vtkSmartPointer::New();
// wndSincSmoothFilter->SetInputConnection(reader->GetOutputPort());
// wndSincSmoothFilter->SetNumberOfIterations(100);
// wndSincSmoothFilter->Update();
vtkSmartPointer<vtkPolyDataMapper> inputMapper =
vtkSmartPointer<vtkPolyDataMapper>::New();
inputMapper->SetInputConnection(reader->GetOutputPort());
vtkSmartPointer<vtkActor> inputActor =
vtkSmartPointer<vtkActor>::New();
inputActor->SetMapper(inputMapper);
vtkSmartPointer<vtkPolyDataMapper> smoothedMapper =
vtkSmartPointer<vtkPolyDataMapper>::New();
smoothedMapper->SetInputConnection(smoothFilter->GetOutputPort());
vtkSmartPointer<vtkActor> smoothedActor =
vtkSmartPointer<vtkActor>::New();
smoothedActor->SetMapper(smoothedMapper);
double leftViewport[4] = { 0.0, 0.0, 0.5, 1.0 };
double rightViewport[4] = { 0.5, 0.0, 1.0, 1.0 };
vtkSmartPointer<vtkRenderer> leftRenderer =
vtkSmartPointer<vtkRenderer>::New();
leftRenderer->SetViewport(leftViewport);
leftRenderer->AddActor(inputActor);
leftRenderer->SetBackground(0.2, 0, .5);
leftRenderer->ResetCamera();
vtkSmartPointer<vtkRenderer> rightRenderer =
vtkSmartPointer<vtkRenderer>::New();
rightRenderer->SetViewport(rightViewport);
rightRenderer->AddActor(smoothedActor);
rightRenderer->SetBackground(0.5, 0.5, 0);
rightRenderer->ResetCamera();
vtkSmartPointer<vtkRenderWindow> rw =
vtkSmartPointer<vtkRenderWindow>::New();
rw->AddRenderer(leftRenderer);
rw->AddRenderer(rightRenderer);
rw->SetSize(640, 320);
rw->SetWindowName("PolyData Grid Smooth By LapLasian");
vtkSmartPointer<vtkRenderWindowInteractor> rwi =
vtkSmartPointer<vtkRenderWindowInteractor>::New();
rwi->SetRenderWindow(rw);
rwi->Initialize();
rwi->Start();
return 0;
}